新人教版九年级上册24.2.1点与圆的位置关系(第一课时)
文档属性
| 名称 | 新人教版九年级上册24.2.1点与圆的位置关系(第一课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 674.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-26 00:00:00 | ||
图片预览







文档简介
课件20张PPT。24.2.1 点与圆的位置关系第一课时情景引入问题:你知道击中靶上不同位置的成绩是如何计算的吗?情景引入把实际问题转化为数学问题:靶上有圆,这些圆圆心相同,半径不同,称为同心圆.击中的位置看作一些点,点的不同位置决定了环数. 通过第一单元的学习,你知道点与圆有几种位置关系吗?请画图说明。发现新知设⊙O的半径为r,点到圆心的距离为d。
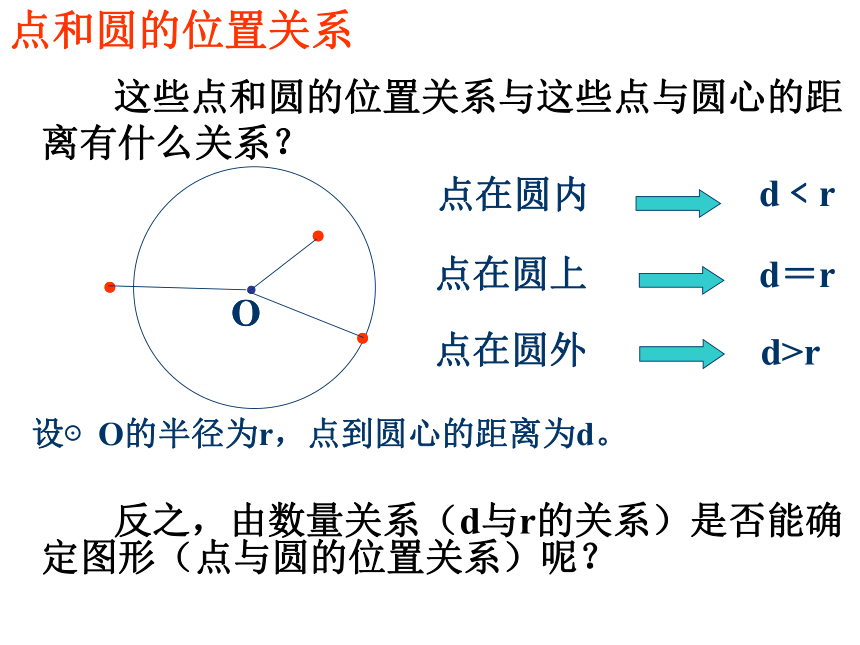
点和圆的位置关系点在圆内d﹤r点在圆上点在圆外d=rd>r●●●●O●●●●O 反之,由数量关系(d与r的关系)是否能确定图形(点与圆的位置关系)呢? 这些点和圆的位置关系与这些点与圆心的距离有什么关系?设⊙O的半径为r,点到圆心的距离为d。则点和圆的位置关系点在圆内d﹤r点在圆上点在圆外d=rd>r●●●●O练习1:
已知圆O的直径等于10厘米,点P到圆心的距离分别是:
(1)8厘米 (2)4厘米 (3)5厘米。
请你分别说出点P与圆O的位置关系。巩固新知练习2:
两个同心圆,大圆的半径R=3cm,小圆的半径r=2cm,点P在小圆外、大圆内,则点P到圆心的距离d的范围是 。
2cm<d<3cm练习3:
已知⊙O的半径为5cm,A是线段OP的中点,
当OP=6cm时,点A在⊙O 。
当OP=10cm时,点A在⊙O 。当OP=12cm时,点A在⊙O 。内上外例1 如图,已知矩形ABCD 的边AB=3cm,AD=4cm。
(1)以点A为圆心,4cm为半径作圆,则点B、C、D与⊙A的位置关系如何?(2)若以点A为圆心作圆,使B、C、D三点中至少有一点在圆内,且至少有一点在圆外,则⊙A 的半径r 的取值范围是什么?典例精析如图,已知Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AC=3,AB=5.
(1)若以C为圆心,AC为半径画圆,试指出A、B、D与⊙ C的位置关系,并说明理由。(2)若以C为圆心画圆,使A、B、D三点至少一个在圆内,一个在圆外,则⊙ C的半径r的取值范围是什么?即时练习 1 . 如图所示,在A地正北60m的B处有一幢
民房,正西80m的C处有一变电设施,在BC的中
点D处是一古建筑。 因施工需要,必须在A处进行一
次爆破。为使民房、变电设施、古建筑都不遭到破
坏,问爆破影响面的半径应控制在什么范围内?60m80m实际应用 2、伦敦奥运冠军郭文珺第一次击中9环,现在你知道成绩是如何计算的吗?实际应用 若击中8环呢? 若击中10环呢?1、已知⊙O的半径为1,点P到O的距离为d,且方程
x2-2x+d=0有实数根d,则点P与⊙O的位置关系是 .2、 ⊙O的半径为5,圆心O的坐标(0,0 ),
点P(4,2)与⊙O的位置关系是 .拓展训练3、如图,海边有两座灯塔A、B,暗礁分布在经过A、B两点的弓形区域内,∠AOB=80°,为了避免触礁,轮船P与A、B的张角∠APB应在什么范围内?拓展训练课堂小结点和圆的位置关系点在圆内d﹤r点在圆上点在圆外d=rd>r设⊙O的半径为r,点到圆心的距离为d,判断方法2今天作业1 作业本(2 ) p23---24课时作业本
P86-87 1、4、7、10、12、13
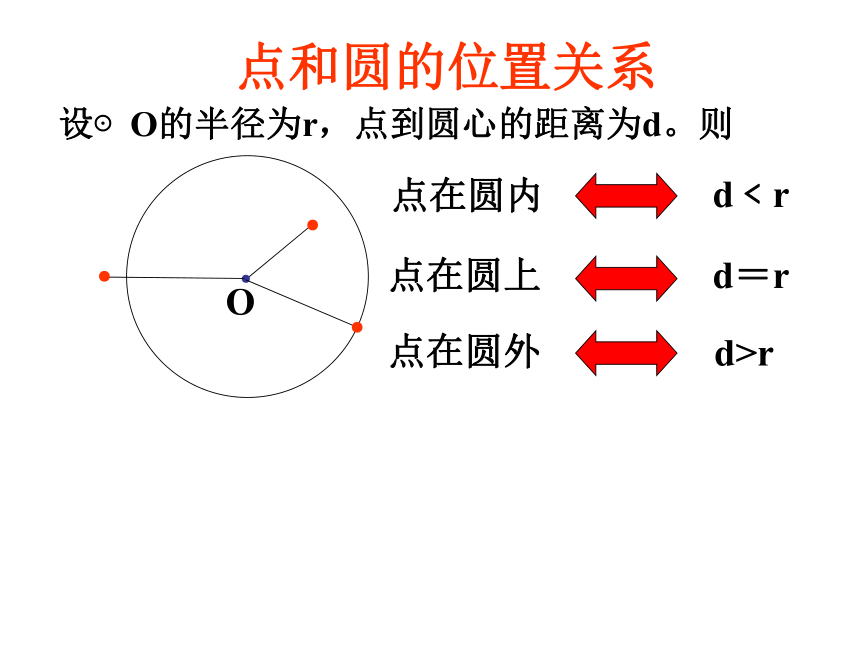
点和圆的位置关系点在圆内d﹤r点在圆上点在圆外d=rd>r●●●●O●●●●O 反之,由数量关系(d与r的关系)是否能确定图形(点与圆的位置关系)呢? 这些点和圆的位置关系与这些点与圆心的距离有什么关系?设⊙O的半径为r,点到圆心的距离为d。则点和圆的位置关系点在圆内d﹤r点在圆上点在圆外d=rd>r●●●●O练习1:
已知圆O的直径等于10厘米,点P到圆心的距离分别是:
(1)8厘米 (2)4厘米 (3)5厘米。
请你分别说出点P与圆O的位置关系。巩固新知练习2:
两个同心圆,大圆的半径R=3cm,小圆的半径r=2cm,点P在小圆外、大圆内,则点P到圆心的距离d的范围是 。
2cm<d<3cm练习3:
已知⊙O的半径为5cm,A是线段OP的中点,
当OP=6cm时,点A在⊙O 。
当OP=10cm时,点A在⊙O 。当OP=12cm时,点A在⊙O 。内上外例1 如图,已知矩形ABCD 的边AB=3cm,AD=4cm。
(1)以点A为圆心,4cm为半径作圆,则点B、C、D与⊙A的位置关系如何?(2)若以点A为圆心作圆,使B、C、D三点中至少有一点在圆内,且至少有一点在圆外,则⊙A 的半径r 的取值范围是什么?典例精析如图,已知Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AC=3,AB=5.
(1)若以C为圆心,AC为半径画圆,试指出A、B、D与⊙ C的位置关系,并说明理由。(2)若以C为圆心画圆,使A、B、D三点至少一个在圆内,一个在圆外,则⊙ C的半径r的取值范围是什么?即时练习 1 . 如图所示,在A地正北60m的B处有一幢
民房,正西80m的C处有一变电设施,在BC的中
点D处是一古建筑。 因施工需要,必须在A处进行一
次爆破。为使民房、变电设施、古建筑都不遭到破
坏,问爆破影响面的半径应控制在什么范围内?60m80m实际应用 2、伦敦奥运冠军郭文珺第一次击中9环,现在你知道成绩是如何计算的吗?实际应用 若击中8环呢? 若击中10环呢?1、已知⊙O的半径为1,点P到O的距离为d,且方程
x2-2x+d=0有实数根d,则点P与⊙O的位置关系是 .2、 ⊙O的半径为5,圆心O的坐标(0,0 ),
点P(4,2)与⊙O的位置关系是 .拓展训练3、如图,海边有两座灯塔A、B,暗礁分布在经过A、B两点的弓形区域内,∠AOB=80°,为了避免触礁,轮船P与A、B的张角∠APB应在什么范围内?拓展训练课堂小结点和圆的位置关系点在圆内d﹤r点在圆上点在圆外d=rd>r设⊙O的半径为r,点到圆心的距离为d,判断方法2今天作业1 作业本(2 ) p23---24课时作业本
P86-87 1、4、7、10、12、13
同课章节目录
