新人教版九年级上册24.2.2 直线与圆的位置关系(第二课时)
文档属性
| 名称 | 新人教版九年级上册24.2.2 直线与圆的位置关系(第二课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 47.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-26 00:00:00 | ||
图片预览


文档简介
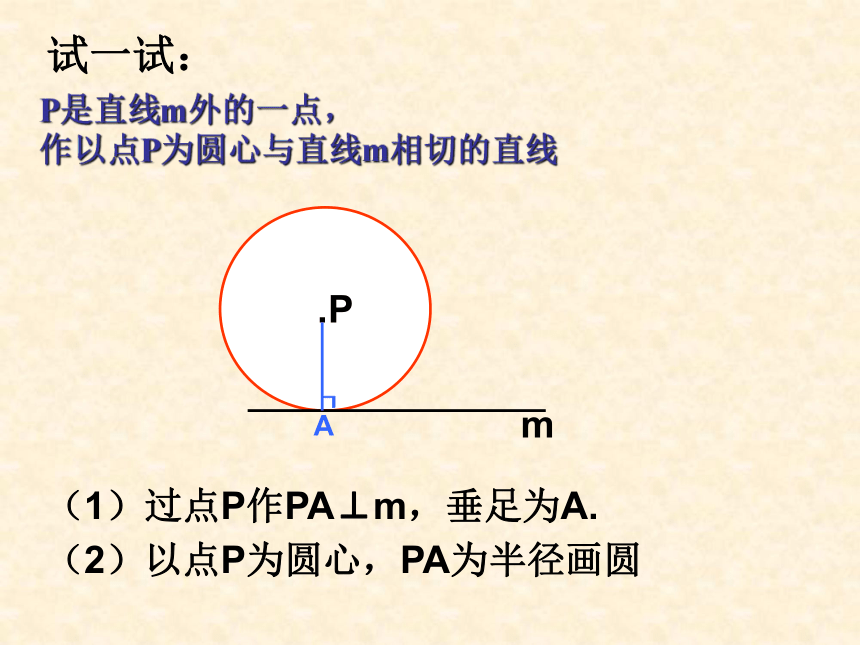
课件21张PPT。24.2.2 直线与圆的位置关系(2)smmbqsmmmmmmmmmmmmmmmP是直线m外的一点,
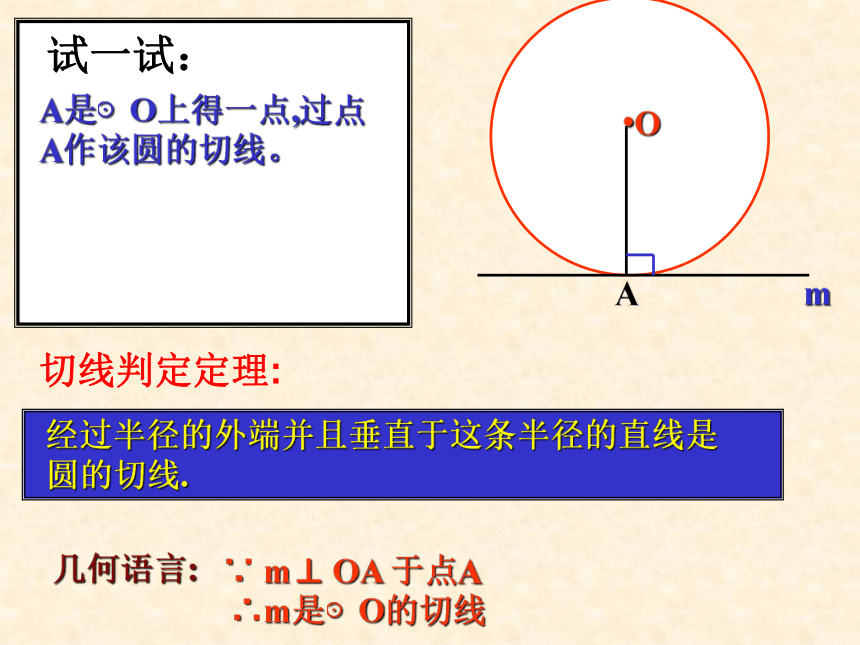
作以点P为圆心与直线m相切的直线试一试:┒A(1)过点P作PA⊥m,垂足为A.(2)以点P为圆心,PA为半径画圆A是⊙O上得一点,过点
A作该圆的切线。.OAm经过半径的外端并且垂直于这条半径的直线是
圆的切线.几何语言: ∵ m⊥ OA 于点A
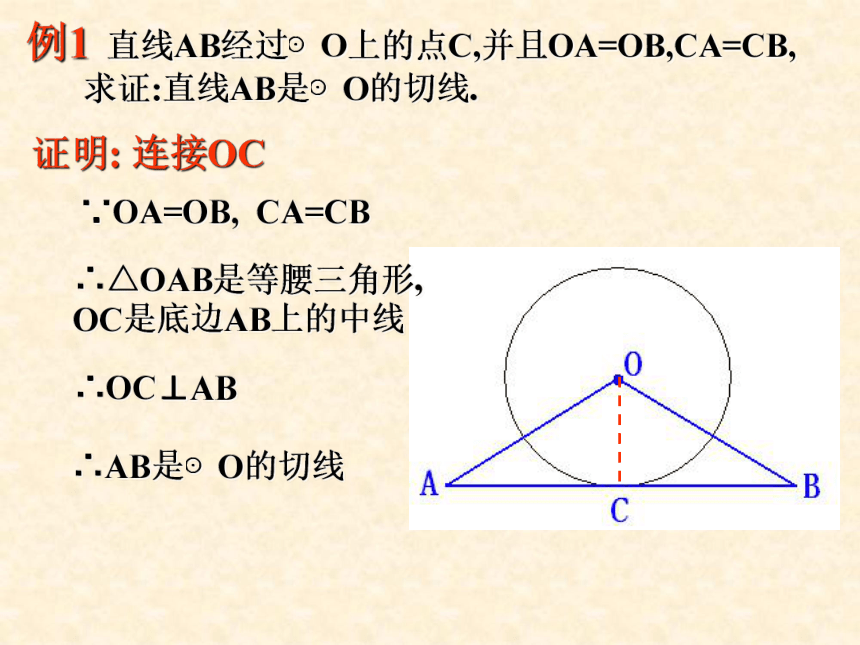
∴m是⊙O的切线切线判定定理:试一试:例1 直线AB经过⊙O上的点C,并且OA=OB,CA=CB,
求证:直线AB是⊙O的切线.证明: 连接OC∵OA=OB, CA=CB∴△OAB是等腰三角形,
OC是底边AB上的中线
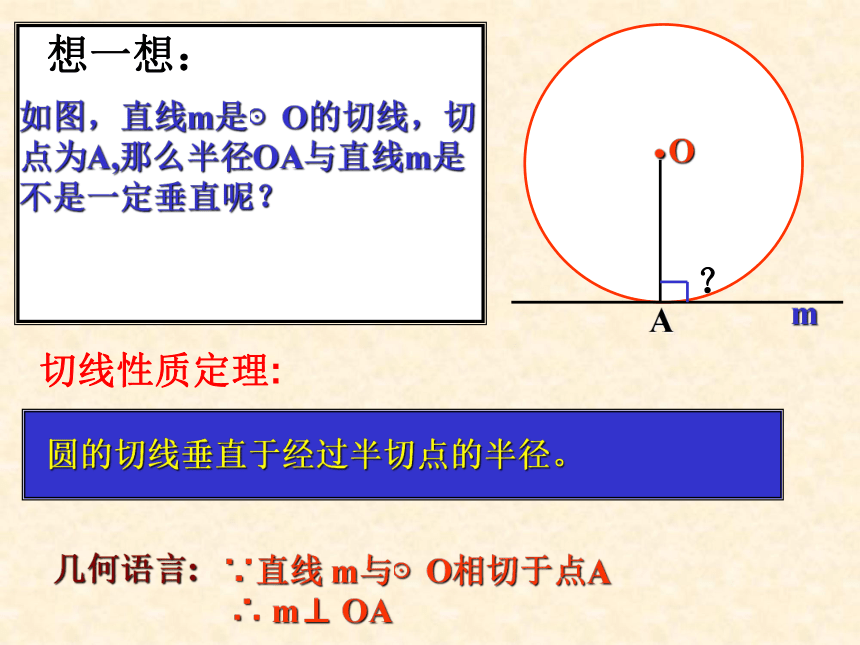
∴OC⊥AB∴AB是⊙O的切线如图,直线m是⊙O的切线,切
点为A,那么半径OA与直线m是不是一定垂直呢?.OAm想一想:?几何语言: ∵直线 m与⊙O相切于点A
∴ m⊥ OA圆的切线垂直于经过半切点的半径。
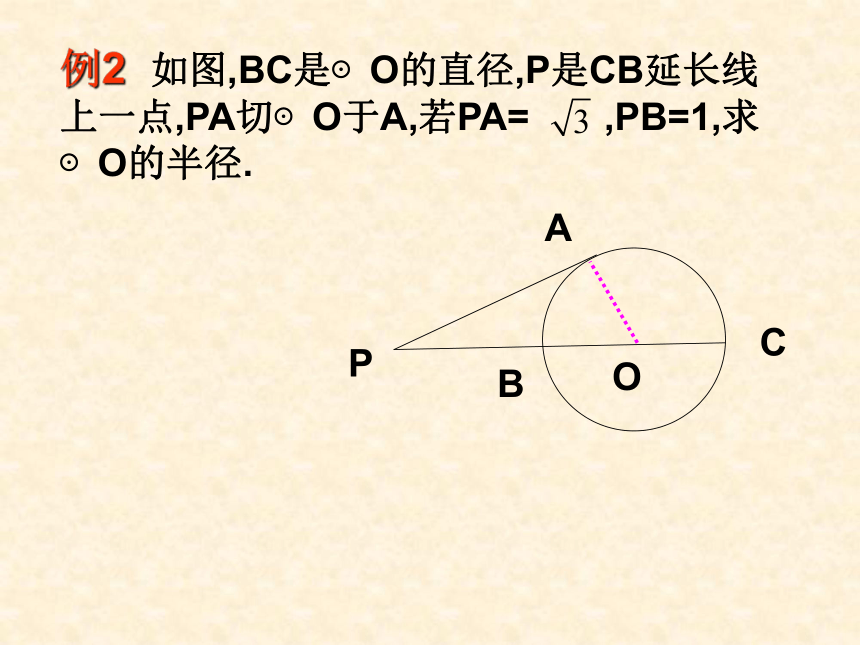
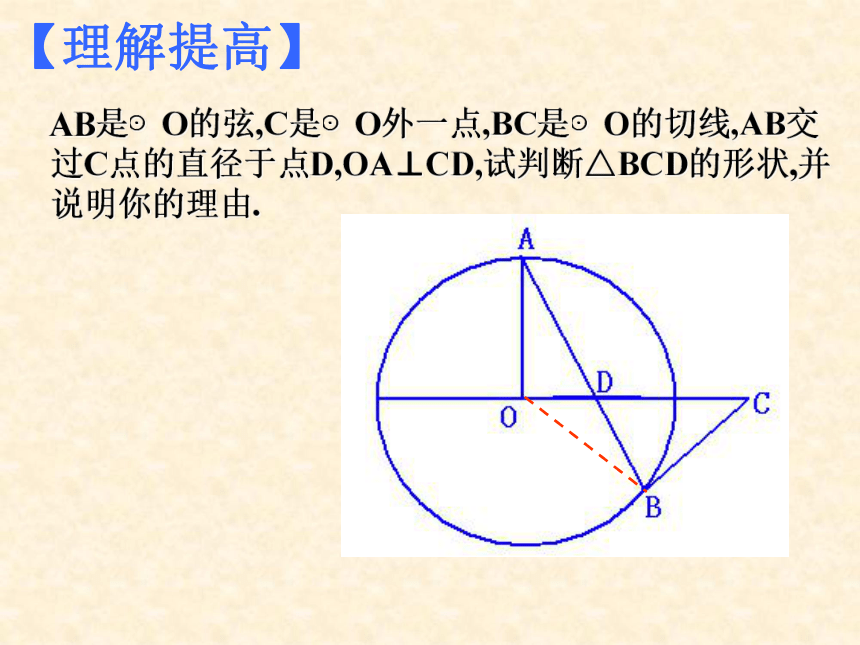
切线性质定理:例2 如图,BC是⊙O的直径,P是CB延长线上一点,PA切⊙O于A,若PA= ,PB=1,求⊙O的半径.ABPOC AB是⊙O的弦,C是⊙O外一点,BC是⊙O的切线,AB交
过C点的直径于点D,OA⊥CD,试判断△BCD的形状,并
说明你的理由.【理解提高】课堂小结1、定义法:和圆有且只有一个公共点的直线是圆的切线。
2、数量法(d=r):和圆心距离等于半径的直线是圆的切线。
3、判定定理:经过半径外端且垂直于这条半径的直线是圆的切线。一、证明直线与圆相切方法1、切线和圆只有一个公共点。2、切线和圆心的距离等于半径。3、切线垂直于过切点的半径。二、切线的性质:练习1: 如图,AB是⊙O的直径,点D在AB的延长线 上,BD=OB,点C在圆上,∠CAB=300.
求证:DC是⊙O的切线.方法引导
当已知直线与圆有公共点,要证明直线与圆相切时,可先连结圆心与公共点,再证明连线垂直于直线 ,这是证明切线的一种方法.练习2: 在Rt△ABC中,∠B=90°,∠A的平分线交BC于D,以D为圆心,DB长为半径作⊙D.试说明:AC是⊙D的切线.F┏方法引导
若直线与圆的公共点未指明,则过圆心作直线的垂线段,然后说明这条线段的长等于圆的半径,这也是证明切线的一种方法.E今天作业1 作业本(1)P24-25课时作业本 P88---89
如图,已知,AB是⊙O直径,BC⊥AB于B,⊙O的弦AD∥OC。
求证:DC是⊙O的切线.练习如图,在梯形ABCD中,AD∥BC, ∠C=90°.且AB=AD+BC,求证:以AB为直径的⊙O与CD相切.ABCDOEAL1L2BO1.如图,AB是⊙O的直径,直线L1、L2是⊙O的切线,A、B是切点,直线L1、L2有怎样的位置关系?
练习ACO2.已知如图,半径为5cm的⊙O切AC于点B,AB=5cm,
BC= cm,求∠AOC的度数.B已知△ABC内接于⊙O,直线EF过点A(1)如图1,AB为直径,要使得EF是⊙O的切线,还需添加的条件是 或 。
(2)如图2, AB为非直径弦,且∠CAE=∠B,求证:EF为⊙O的切线。一般情况下,要证明一条直线为圆的切线,它过半径外端(即一点已在圆上)是已知给出时,只需证明直线垂直于这条半径。4.AB是⊙O的直径,AE平分∠BAC交⊙O于点E,过点E
作⊙O的切线交AC于点D,试判断△AED的形状,并
说明理由.6.小红家的锅盖坏了,为了配一个锅盖,需要测量锅盖(锅边
所形成的圆) 的直径,而小红家只有一把长20cm 的直尺,
根本不够长,怎么办呢?
小红想了想,采取以下方法:
首先把锅平放到墙根,锅边刚好靠到两墙,用直尺紧贴墙面
量得MA的长,即可求出锅盖的直径,请你利用下图,说明她
这样做的道理. O 如图所示,△ABC中,AC=BC,以BC为直径的⊙O交AB于D,过点D作DE⊥AC于点E,交BC的延长线于点F.
求证:(1)AD=BD;
(2)DF是⊙O的切线.能力与拓展
作以点P为圆心与直线m相切的直线试一试:┒A(1)过点P作PA⊥m,垂足为A.(2)以点P为圆心,PA为半径画圆A是⊙O上得一点,过点
A作该圆的切线。.OAm经过半径的外端并且垂直于这条半径的直线是
圆的切线.几何语言: ∵ m⊥ OA 于点A
∴m是⊙O的切线切线判定定理:试一试:例1 直线AB经过⊙O上的点C,并且OA=OB,CA=CB,
求证:直线AB是⊙O的切线.证明: 连接OC∵OA=OB, CA=CB∴△OAB是等腰三角形,
OC是底边AB上的中线
∴OC⊥AB∴AB是⊙O的切线如图,直线m是⊙O的切线,切
点为A,那么半径OA与直线m是不是一定垂直呢?.OAm想一想:?几何语言: ∵直线 m与⊙O相切于点A
∴ m⊥ OA圆的切线垂直于经过半切点的半径。
切线性质定理:例2 如图,BC是⊙O的直径,P是CB延长线上一点,PA切⊙O于A,若PA= ,PB=1,求⊙O的半径.ABPOC AB是⊙O的弦,C是⊙O外一点,BC是⊙O的切线,AB交
过C点的直径于点D,OA⊥CD,试判断△BCD的形状,并
说明你的理由.【理解提高】课堂小结1、定义法:和圆有且只有一个公共点的直线是圆的切线。
2、数量法(d=r):和圆心距离等于半径的直线是圆的切线。
3、判定定理:经过半径外端且垂直于这条半径的直线是圆的切线。一、证明直线与圆相切方法1、切线和圆只有一个公共点。2、切线和圆心的距离等于半径。3、切线垂直于过切点的半径。二、切线的性质:练习1: 如图,AB是⊙O的直径,点D在AB的延长线 上,BD=OB,点C在圆上,∠CAB=300.
求证:DC是⊙O的切线.方法引导
当已知直线与圆有公共点,要证明直线与圆相切时,可先连结圆心与公共点,再证明连线垂直于直线 ,这是证明切线的一种方法.练习2: 在Rt△ABC中,∠B=90°,∠A的平分线交BC于D,以D为圆心,DB长为半径作⊙D.试说明:AC是⊙D的切线.F┏方法引导
若直线与圆的公共点未指明,则过圆心作直线的垂线段,然后说明这条线段的长等于圆的半径,这也是证明切线的一种方法.E今天作业1 作业本(1)P24-25课时作业本 P88---89
如图,已知,AB是⊙O直径,BC⊥AB于B,⊙O的弦AD∥OC。
求证:DC是⊙O的切线.练习如图,在梯形ABCD中,AD∥BC, ∠C=90°.且AB=AD+BC,求证:以AB为直径的⊙O与CD相切.ABCDOEAL1L2BO1.如图,AB是⊙O的直径,直线L1、L2是⊙O的切线,A、B是切点,直线L1、L2有怎样的位置关系?
练习ACO2.已知如图,半径为5cm的⊙O切AC于点B,AB=5cm,
BC= cm,求∠AOC的度数.B已知△ABC内接于⊙O,直线EF过点A(1)如图1,AB为直径,要使得EF是⊙O的切线,还需添加的条件是 或 。
(2)如图2, AB为非直径弦,且∠CAE=∠B,求证:EF为⊙O的切线。一般情况下,要证明一条直线为圆的切线,它过半径外端(即一点已在圆上)是已知给出时,只需证明直线垂直于这条半径。4.AB是⊙O的直径,AE平分∠BAC交⊙O于点E,过点E
作⊙O的切线交AC于点D,试判断△AED的形状,并
说明理由.6.小红家的锅盖坏了,为了配一个锅盖,需要测量锅盖(锅边
所形成的圆) 的直径,而小红家只有一把长20cm 的直尺,
根本不够长,怎么办呢?
小红想了想,采取以下方法:
首先把锅平放到墙根,锅边刚好靠到两墙,用直尺紧贴墙面
量得MA的长,即可求出锅盖的直径,请你利用下图,说明她
这样做的道理. O 如图所示,△ABC中,AC=BC,以BC为直径的⊙O交AB于D,过点D作DE⊥AC于点E,交BC的延长线于点F.
求证:(1)AD=BD;
(2)DF是⊙O的切线.能力与拓展
同课章节目录
