新人教版九年级上册4.2.2 直线与圆的位置关系(第三课时)
文档属性
| 名称 | 新人教版九年级上册4.2.2 直线与圆的位置关系(第三课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 98.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-26 00:00:00 | ||
图片预览


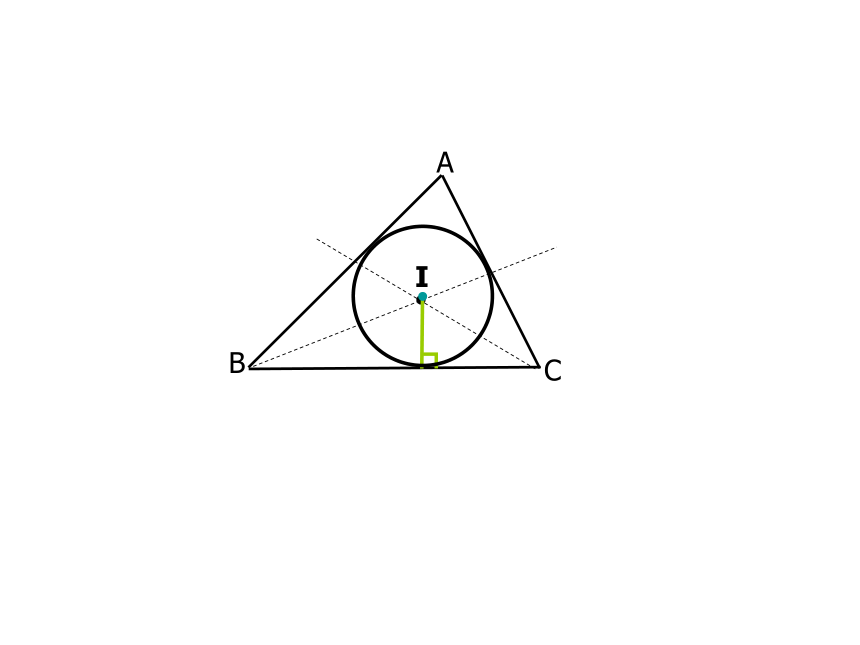
文档简介
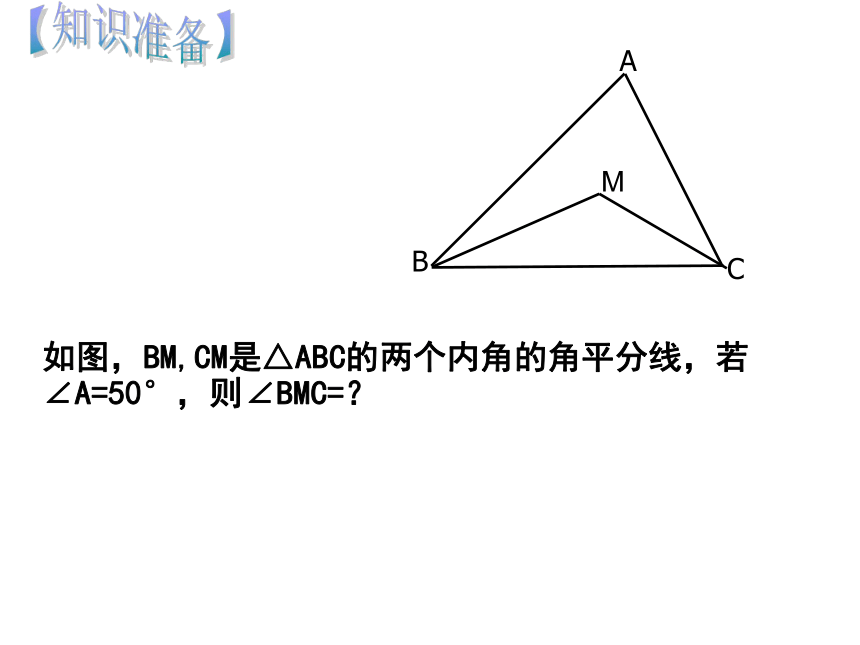
课件30张PPT。24.2.2 直线与圆的位置关系(3)【知识准备】 如图,BM,CM是△ABC的两个内角的角平分线,若∠A=50°,则∠BMC=?
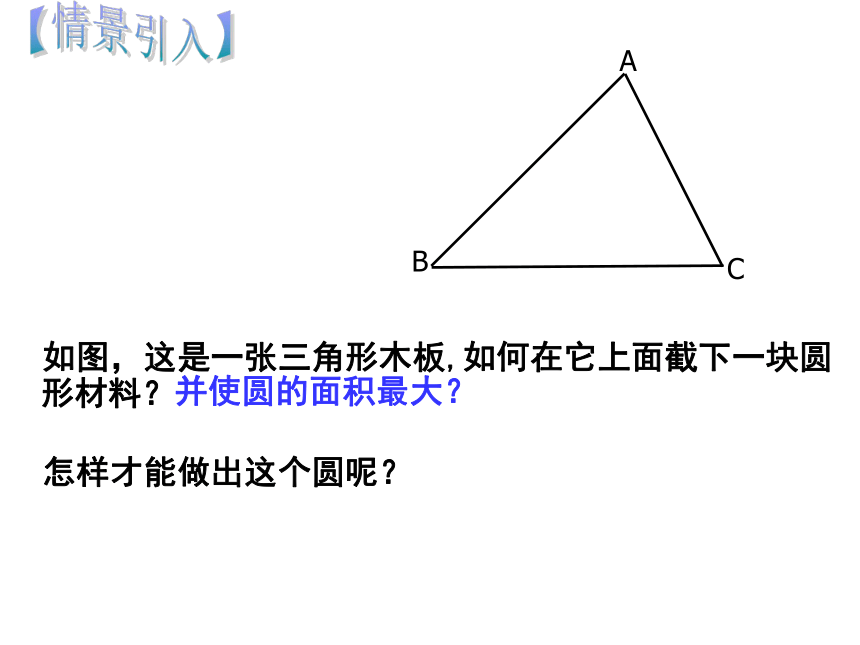
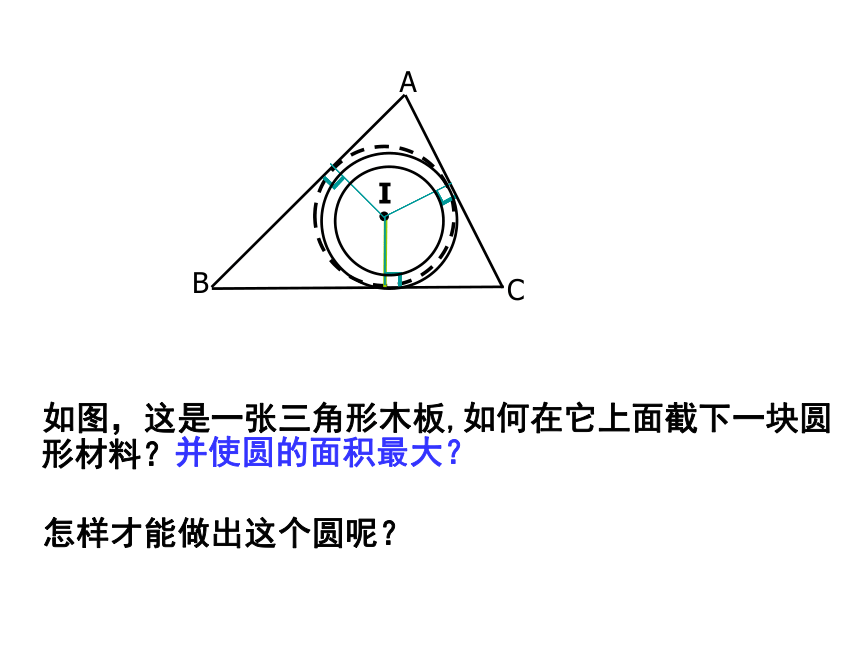
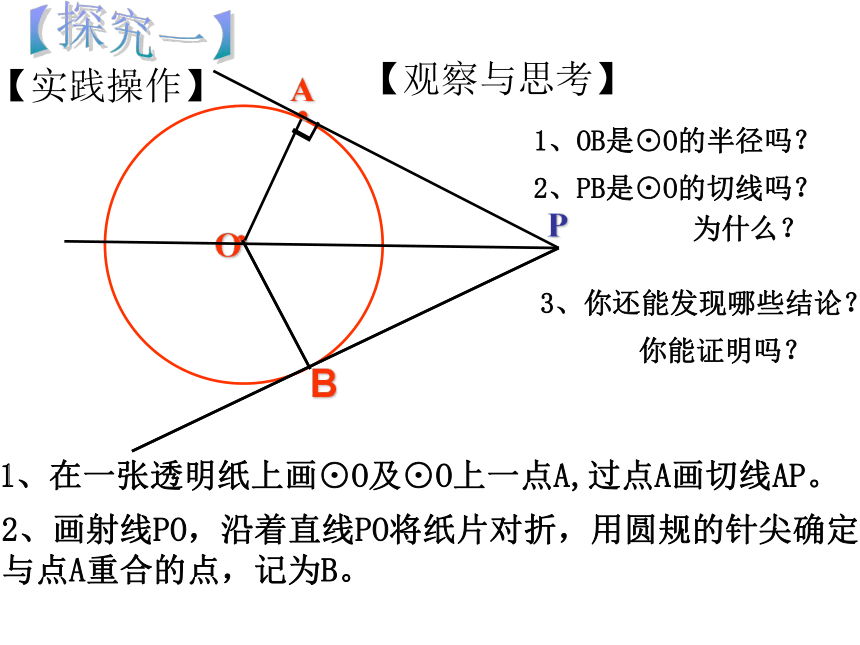
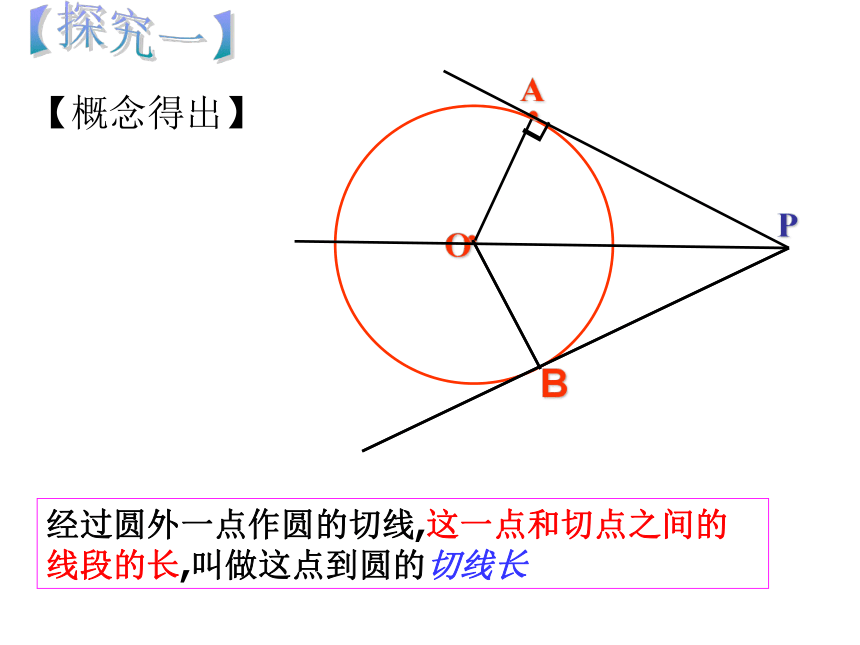
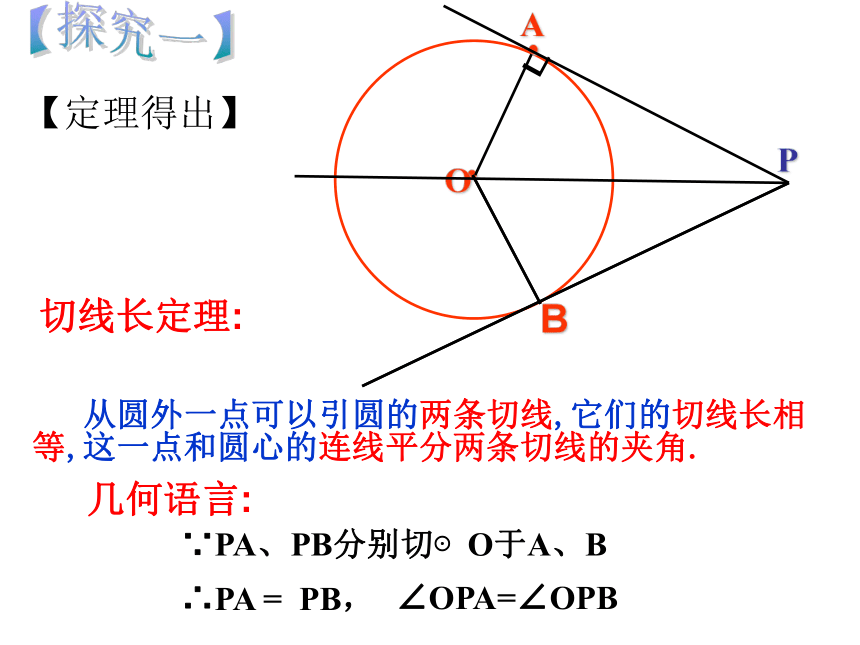
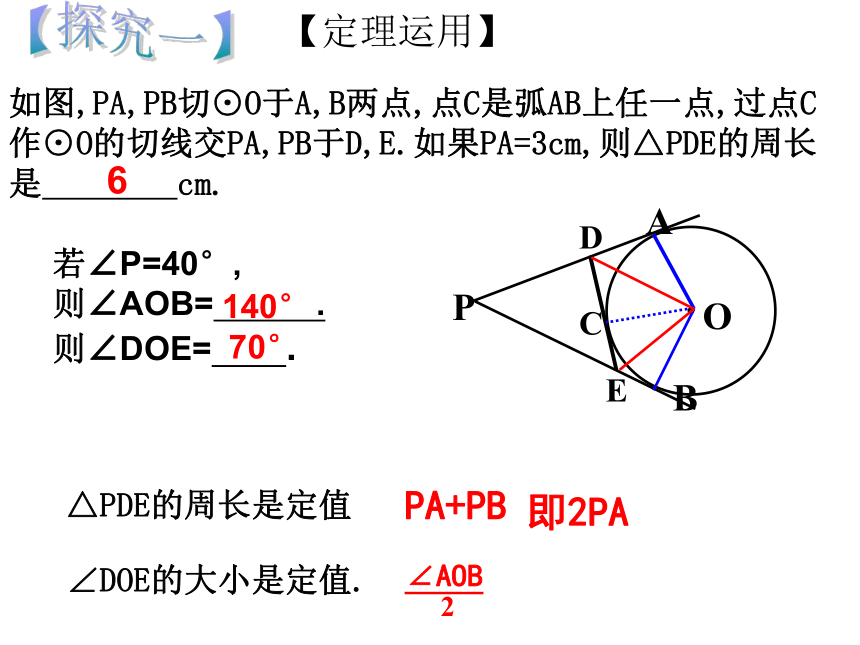
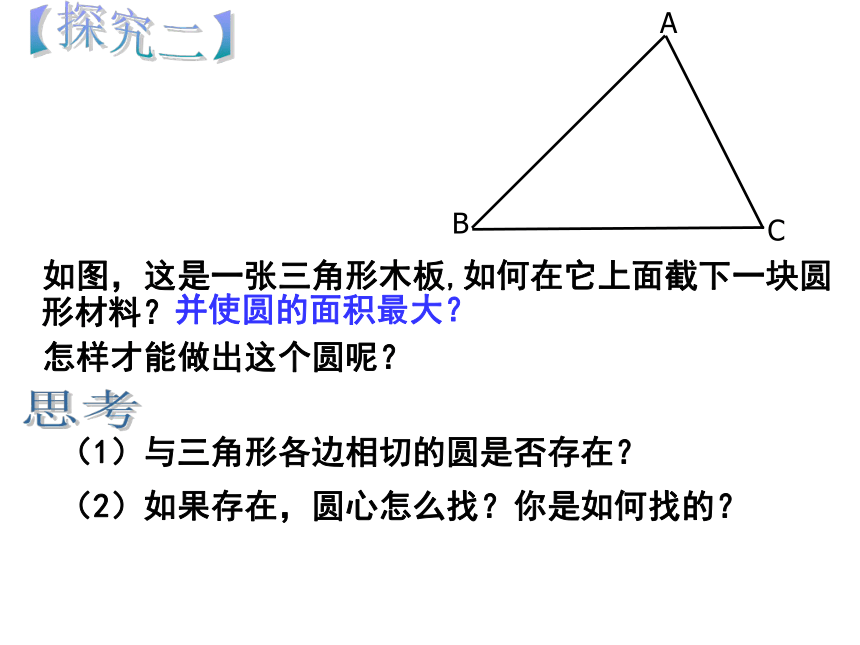
如图,这是一张三角形木板,如何在它上面截下一块圆形材料? 并使圆的面积最大? 怎样才能做出这个圆呢?【情景引入】I● 如图,这是一张三角形木板,如何在它上面截下一块圆形材料? 并使圆的面积最大? 怎样才能做出这个圆呢?24.2.2三角形的内切圆P【探究一】1、在一张透明纸上画⊙O及⊙O上一点A,过点A画切线AP。2、画射线PO,沿着直线PO将纸片对折,用圆规的针尖确定与点A重合的点,记为B。┖1、OB是⊙O的半径吗?【实践操作】【观察与思考】2、PB是⊙O的切线吗?为什么?3、你还能发现哪些结论?你能证明吗?【探究一】【概念得出】经过圆外一点作圆的切线,这一点和切点之间的线段的长,叫做这点到圆的切线长【探究一】【定理得出】 从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角. 切线长定理:几何语言:∵PA、PB分别切⊙O于A、B∴PA = PB,∠OPA=∠OPB如图,PA,PB切⊙O于A,B两点,点C是弧AB上任一点,过点C
作⊙O的切线交PA,PB于D,E.如果PA=3cm,则△PDE的周长
是 cm.DCEOPAB若∠P=40°,
则∠AOB= .
则∠DOE= .
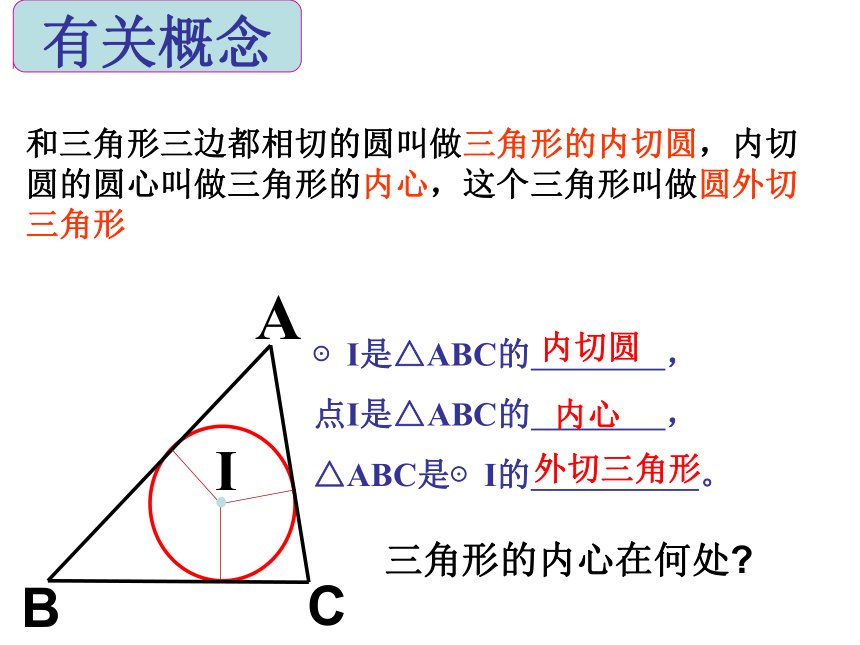
△PDE的周长是定值PA+PB∠DOE的大小是定值.140°6即2PA【探究一】【定理运用】70° 如图,这是一张三角形木板,如何在它上面截下一块圆形材料? 并使圆的面积最大? 怎样才能做出这个圆呢?【探究二】 (1)与三角形各边相切的圆是否存在?思考 (2)如果存在,圆心怎么找?你是如何找的?I●和三角形三边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆外切三角形有关概念⊙I是△ABC的 ,
点I是△ABC的 ,
△ABC是⊙I的 。内切圆内心外切三角形三角形的内心在何处? 1、 如图1,△ABC是⊙O的 三角形。⊙ O是△ABC的 圆,点O叫△ABC的 ,它是三角形 _ _ _ _ _ _ _ _ _ 的交点。外接内接外心三边垂直平分线2、如图2,△DEF是⊙I的 三角形, ⊙I是△DEF的 圆,点I是 △DEF的 心,它是_ __ _ _ __ _的交点。外切内切内角平分线类比学习三角形内心的特征: 三角形的内心到三角形各边的距离相等; 三角形的外心到三角形各个 顶点的距离相等;
三角形外心的特征:类比学习【自主练习】 1、如图,点O是△ABC的内心,若∠ABC=50°, ∠ACB=70°则∠BOC=?变式:若∠A=80°, 则∠BOC=?【自主练习】2、如图,△ABC的内切圆的半径为r,△ABC的周长为ι,求△ABC的面积。
【探究二】直角三角形、钝角三角形的内切圆是否存在?若存在,请你画出来,并观察内心的位置。例 已知:在△ABC中,BC=14cm,AC=9cm,AB=13cm,它的内切圆分别和BC、AC、AB切于点D、E、F,求AF、BD和CE的长。ABCFDExx13-x13-x9-x9-x【应用拓展】变式:若△ABC是直角三角形, ∠ACB=90°,AB=13cm,AC=5cm,求它的内切圆半径。0BDEACF变式:若△ABC是直角三角形, ∠ACB=90°,AB=13cm,AC=5cm,求它的内切圆半径。a,b是直角边,c是斜边。如图, ⊙O是△ABC的内切圆,D,E,F是切点。【检测练习】(1)若AB=8,BC=6,AC=4.求AD、BE、CF的长。(2)若△ABC的周长是36,面积是18,求内切圆的半径。.o如图, ⊙O是△ABC的内切圆,D,E,F是切点。【检测练习】(3)若BE=3,CE=2, △ABC 的周长为18,求AB的长。.o课堂小结:1 切线长概念2 切线长定理从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角. 3 三角形的内切圆、内心4 直角三角形的内切圆半径与三边长之间的关系5 用代数的方法解决几何问题是一种很好的方法。内心 位置:三条角平分线的交点.特征:到三边距离相等。 外心 位置:三条中垂线的交点.特征:到三个顶点距离相等。 今天作业:1 作业本(2) P25---262 课时作业本 P90-91同学们再见!例1:如图,AB是⊙O的直径,AC,BD,CD都是⊙O的切线,A,B,E是切点,连接CO,DO.
求证(1) AC+BD=CD
(2) ∠DOC=90°ABCDOE1、已知直角梯形 ABCD 中,AD∥BC,AB⊥BC,以腰DC的中点 E 为圆心的圆与 AB 相切,梯形的上底 AD与下底 BC 是方程
x 2-10x + 16 = 0的两根,求 ⊙E 的半径 r .F练习:书本P98 1,2想一想:圆的外切四边形的两组对边有什么关系?说明你的结论的正确性.ABCDOLMNP切线长定理的基本图形的研究PA、PB是⊙O的两条切线,A、B为切点,直线OP交于⊙O于点D、E,交AB于C。(1)写出图中所有的垂直关系OA⊥PA,OB ⊥PB,AB ⊥OP(3)写出图中所有的全等三角形△AOP≌ △BOP, △AOC≌ △BOC, △ACP≌ △BCP(4)写出图中所有的等腰三角形△ABP △AOB(2)写出图中与∠AOC相等的角∠AOC=∠BOC=∠PAC=∠PBC算一算:
如果 PA = 4 cm , PD = 2 cm , 求半径 OA 的长.算一算:
如果, ∠APB=50°,则∠AOB是多少度?
如图,这是一张三角形木板,如何在它上面截下一块圆形材料? 并使圆的面积最大? 怎样才能做出这个圆呢?【情景引入】I● 如图,这是一张三角形木板,如何在它上面截下一块圆形材料? 并使圆的面积最大? 怎样才能做出这个圆呢?24.2.2三角形的内切圆P【探究一】1、在一张透明纸上画⊙O及⊙O上一点A,过点A画切线AP。2、画射线PO,沿着直线PO将纸片对折,用圆规的针尖确定与点A重合的点,记为B。┖1、OB是⊙O的半径吗?【实践操作】【观察与思考】2、PB是⊙O的切线吗?为什么?3、你还能发现哪些结论?你能证明吗?【探究一】【概念得出】经过圆外一点作圆的切线,这一点和切点之间的线段的长,叫做这点到圆的切线长【探究一】【定理得出】 从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角. 切线长定理:几何语言:∵PA、PB分别切⊙O于A、B∴PA = PB,∠OPA=∠OPB如图,PA,PB切⊙O于A,B两点,点C是弧AB上任一点,过点C
作⊙O的切线交PA,PB于D,E.如果PA=3cm,则△PDE的周长
是 cm.DCEOPAB若∠P=40°,
则∠AOB= .
则∠DOE= .
△PDE的周长是定值PA+PB∠DOE的大小是定值.140°6即2PA【探究一】【定理运用】70° 如图,这是一张三角形木板,如何在它上面截下一块圆形材料? 并使圆的面积最大? 怎样才能做出这个圆呢?【探究二】 (1)与三角形各边相切的圆是否存在?思考 (2)如果存在,圆心怎么找?你是如何找的?I●和三角形三边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆外切三角形有关概念⊙I是△ABC的 ,
点I是△ABC的 ,
△ABC是⊙I的 。内切圆内心外切三角形三角形的内心在何处? 1、 如图1,△ABC是⊙O的 三角形。⊙ O是△ABC的 圆,点O叫△ABC的 ,它是三角形 _ _ _ _ _ _ _ _ _ 的交点。外接内接外心三边垂直平分线2、如图2,△DEF是⊙I的 三角形, ⊙I是△DEF的 圆,点I是 △DEF的 心,它是_ __ _ _ __ _的交点。外切内切内角平分线类比学习三角形内心的特征: 三角形的内心到三角形各边的距离相等; 三角形的外心到三角形各个 顶点的距离相等;
三角形外心的特征:类比学习【自主练习】 1、如图,点O是△ABC的内心,若∠ABC=50°, ∠ACB=70°则∠BOC=?变式:若∠A=80°, 则∠BOC=?【自主练习】2、如图,△ABC的内切圆的半径为r,△ABC的周长为ι,求△ABC的面积。
【探究二】直角三角形、钝角三角形的内切圆是否存在?若存在,请你画出来,并观察内心的位置。例 已知:在△ABC中,BC=14cm,AC=9cm,AB=13cm,它的内切圆分别和BC、AC、AB切于点D、E、F,求AF、BD和CE的长。ABCFDExx13-x13-x9-x9-x【应用拓展】变式:若△ABC是直角三角形, ∠ACB=90°,AB=13cm,AC=5cm,求它的内切圆半径。0BDEACF变式:若△ABC是直角三角形, ∠ACB=90°,AB=13cm,AC=5cm,求它的内切圆半径。a,b是直角边,c是斜边。如图, ⊙O是△ABC的内切圆,D,E,F是切点。【检测练习】(1)若AB=8,BC=6,AC=4.求AD、BE、CF的长。(2)若△ABC的周长是36,面积是18,求内切圆的半径。.o如图, ⊙O是△ABC的内切圆,D,E,F是切点。【检测练习】(3)若BE=3,CE=2, △ABC 的周长为18,求AB的长。.o课堂小结:1 切线长概念2 切线长定理从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角. 3 三角形的内切圆、内心4 直角三角形的内切圆半径与三边长之间的关系5 用代数的方法解决几何问题是一种很好的方法。内心 位置:三条角平分线的交点.特征:到三边距离相等。 外心 位置:三条中垂线的交点.特征:到三个顶点距离相等。 今天作业:1 作业本(2) P25---262 课时作业本 P90-91同学们再见!例1:如图,AB是⊙O的直径,AC,BD,CD都是⊙O的切线,A,B,E是切点,连接CO,DO.
求证(1) AC+BD=CD
(2) ∠DOC=90°ABCDOE1、已知直角梯形 ABCD 中,AD∥BC,AB⊥BC,以腰DC的中点 E 为圆心的圆与 AB 相切,梯形的上底 AD与下底 BC 是方程
x 2-10x + 16 = 0的两根,求 ⊙E 的半径 r .F练习:书本P98 1,2想一想:圆的外切四边形的两组对边有什么关系?说明你的结论的正确性.ABCDOLMNP切线长定理的基本图形的研究PA、PB是⊙O的两条切线,A、B为切点,直线OP交于⊙O于点D、E,交AB于C。(1)写出图中所有的垂直关系OA⊥PA,OB ⊥PB,AB ⊥OP(3)写出图中所有的全等三角形△AOP≌ △BOP, △AOC≌ △BOC, △ACP≌ △BCP(4)写出图中所有的等腰三角形△ABP △AOB(2)写出图中与∠AOC相等的角∠AOC=∠BOC=∠PAC=∠PBC算一算:
如果 PA = 4 cm , PD = 2 cm , 求半径 OA 的长.算一算:
如果, ∠APB=50°,则∠AOB是多少度?
同课章节目录
