新人教版九年级上册24.1.4圆周角(第二课时)
文档属性
| 名称 | 新人教版九年级上册24.1.4圆周角(第二课时) |  | |
| 格式 | zip | ||
| 文件大小 | 100.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-26 22:07:19 | ||
图片预览



文档简介
课件21张PPT。24.1.4 圆周角
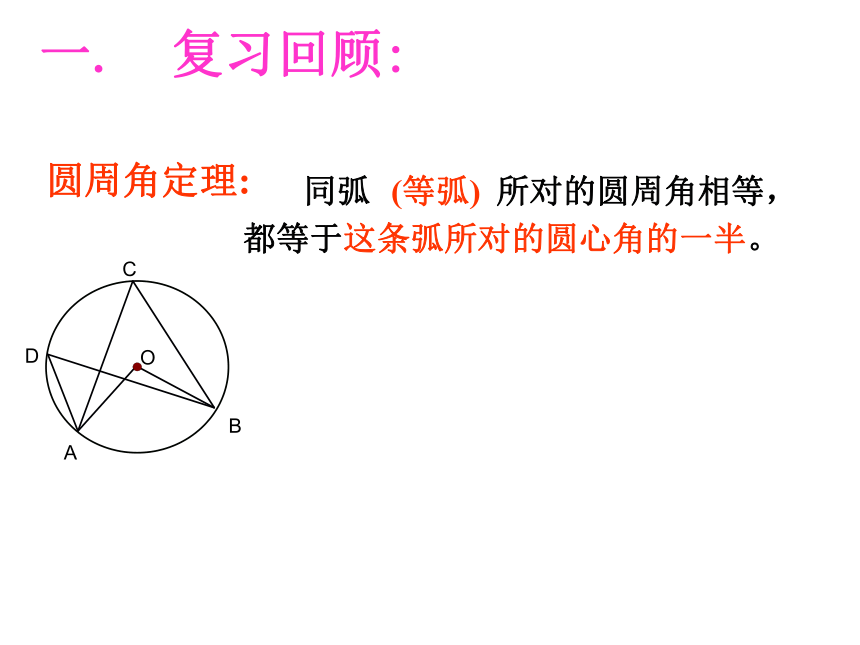
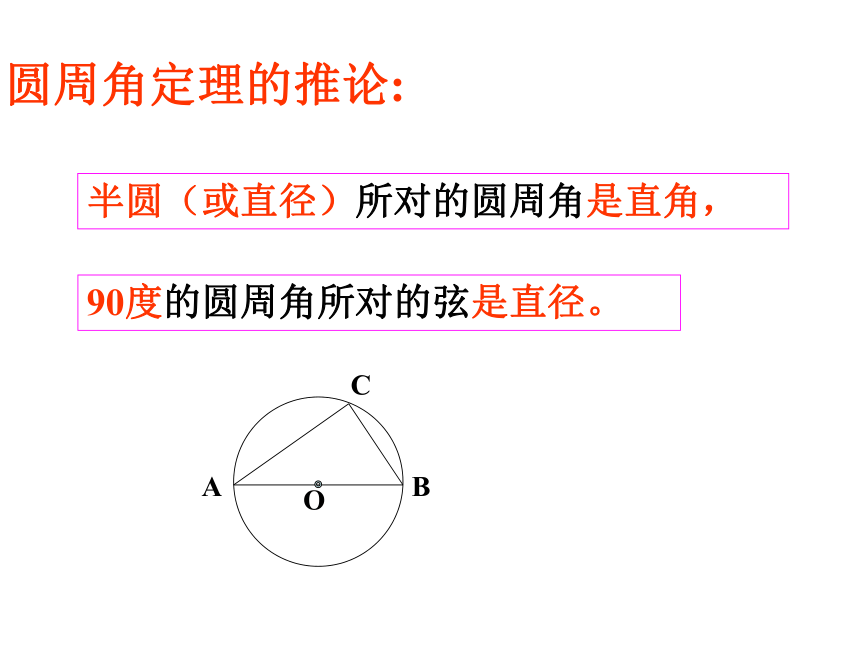
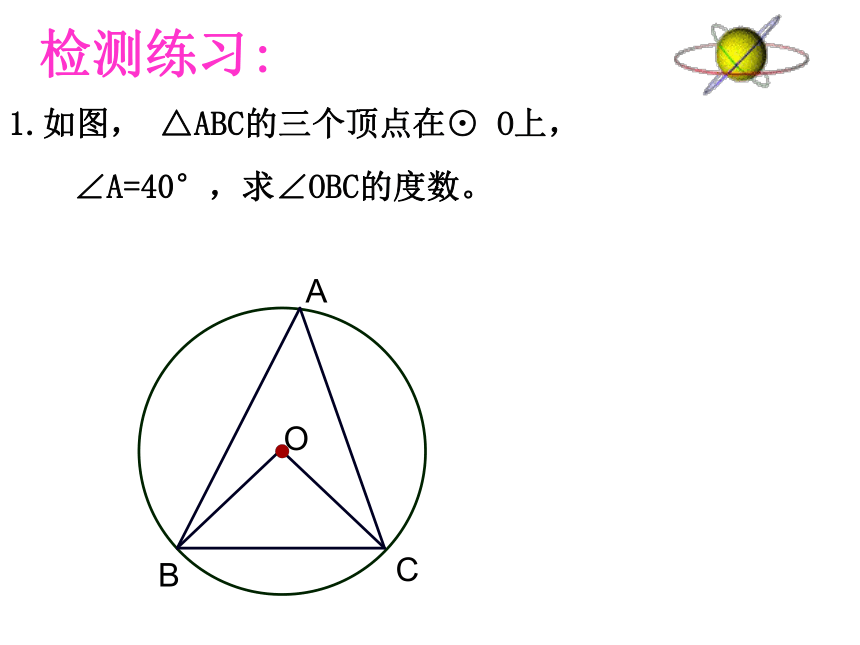
第二课时同弧 所对的圆周角相等,(等弧)都等于这条弧所对的圆心角的一半。圆周角定理:一. 复习回顾:半圆(或直径)所对的圆周角是直角,90度的圆周角所对的弦是直径。圆周角定理的推论:1.如图, △ABC的三个顶点在⊙ O上, ∠A=40°,求∠OBC的度数。 检测练习:2、如图 AB是⊙O的直径, C ,D是圆上的两点,若∠ABD=40°,则∠BCD=_____.40°检测练习:已知中有直径,则作出直径所对的圆周角是一种常见的辅助线。请牢记3、已知⊙O中弦AB的长等于半径,
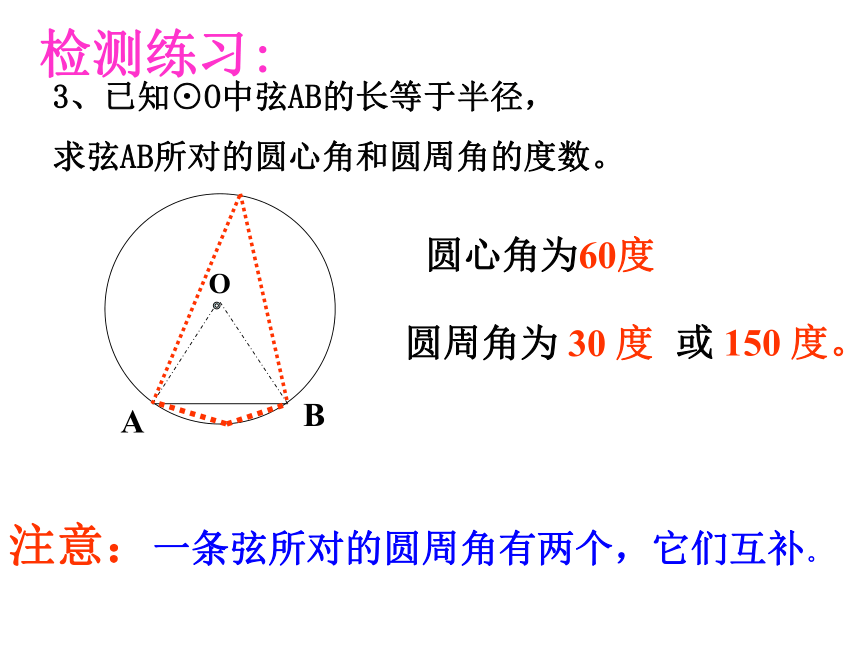
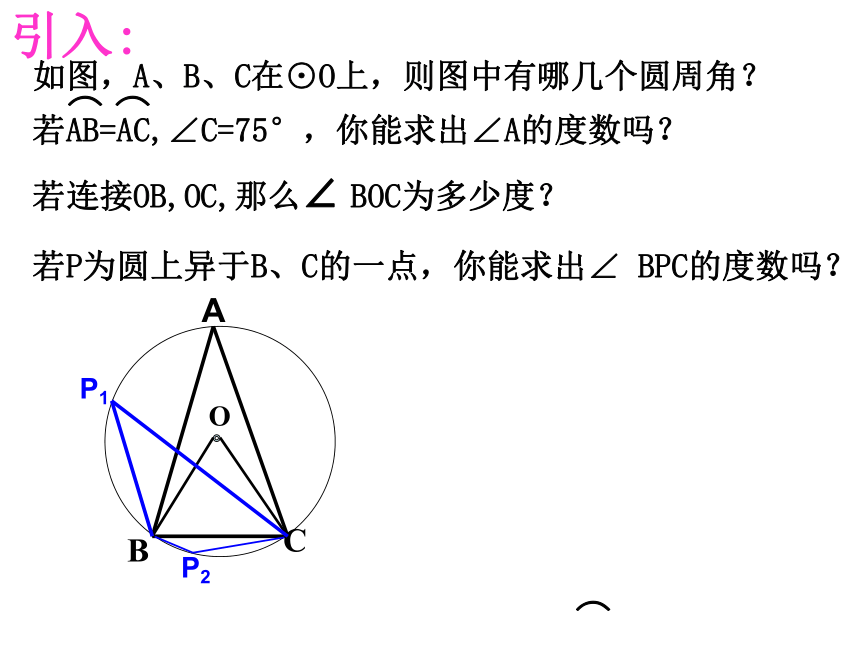
求弦AB所对的圆心角和圆周角的度数。 圆心角为60度圆周角为 30 度或 150 度。检测练习:注意:一条弦所对的圆周角有两个,它们互补。4、求证:如果一个三角形一边上的中线等于该边的一半,那么这个三角形是直角三角形。检测练习:证明三角形是直角三角形的有一种方法。请牢记如图,A、B、C在⊙O上,则图中有哪几个圆周角?OBCA⌒若P为圆上异于B、C的一点,你能求出∠ BPC的度数吗?P1若连接OB,OC,那么∠ BOC为多少度?P2引入:二. 探索新知:OAB1、圆内接四边形,四边形外接圆如图,在圆上分别取A、B、C、D,
并顺次连接,这样我们得到一个四边形ABCD.我们把
四个顶点都在圆上的四边形叫做圆内接四边形,这个圆叫做四边形的外接圆。CD你能给圆内接多边形,多边形外接圆下一个定义吗?类比学习:二. 探索新知:2、想一想:(1)如图,四边形ABCD为⊙O的内接四边形,若∠B=80 ° ,你能求出∠ ADC的度数吗?(2)若∠B=70 ° ,
你能求出∠ ADC的度数吗?(3)若∠B=120 ° ,
你能求出∠ ADC的度数吗?(4)由此你能发现∠B与∠ ADC的关系吗? 你能证明你的猜想吗?二. 探索新知:3、试一试
(1)求下图中各个x、 y的值。(2)若四边形ABCD内接于⊙ O,且∠A:∠B:∠C=1:2:5,则∠D= 。三.应用新知:例1、如图, ⊙ C经过坐标原点,且与两坐标轴分别交于点A、B,点A的坐标为(0,4),M为圆上一点, ∠ BMO=135 ° ,求⊙ C的半径及点C的坐标.┒N例2、如图,AD是△ABC的外角∠ EAC的平分线,
AD与△ABC的外接圆交于点D。
求证:DB=DC.三.应用新知:三.应用新知:练习如图,AD是圆O的直径,BC=CD, ∠BAD=40 °,求∠B的度数。 这节课你在知识学习和探究方法方面有什么收获?四.课堂小结:还有哪些疑惑? 1、作业本(1) P22四.今天作业:2、课时作业本 P82---83五.拓展提高:课时作业本p83 第9题ABCD1、在同圆或等圆中,相等的圆周角所对的弧相等..O五.拓展提高:5、如图,AB是圆O的直径,CD⊥AB,垂足为E,若 ∠ACD=30 °,AE=2cm.求DB的长。你还有其它的解法吗?检测练习:2、 如图1,AB和CD都是⊙O的直径,∠AOC=50°,则∠C的度数是_____ .
3、如图2,已知CD为⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠C的度数是_____ .图1图225° 25° 检测练习:3、已知⊙O中弦AB的长等于半径,
求弦AB所对的圆心角和圆周角的度数。 圆心角为60度圆周角为 30 度或 150 度。变式:已知⊙O的弦AB将将圆周分成1:3的两条弧,求弦AB所对的圆心角和圆周角的度数。 检测练习:
第二课时同弧 所对的圆周角相等,(等弧)都等于这条弧所对的圆心角的一半。圆周角定理:一. 复习回顾:半圆(或直径)所对的圆周角是直角,90度的圆周角所对的弦是直径。圆周角定理的推论:1.如图, △ABC的三个顶点在⊙ O上, ∠A=40°,求∠OBC的度数。 检测练习:2、如图 AB是⊙O的直径, C ,D是圆上的两点,若∠ABD=40°,则∠BCD=_____.40°检测练习:已知中有直径,则作出直径所对的圆周角是一种常见的辅助线。请牢记3、已知⊙O中弦AB的长等于半径,
求弦AB所对的圆心角和圆周角的度数。 圆心角为60度圆周角为 30 度或 150 度。检测练习:注意:一条弦所对的圆周角有两个,它们互补。4、求证:如果一个三角形一边上的中线等于该边的一半,那么这个三角形是直角三角形。检测练习:证明三角形是直角三角形的有一种方法。请牢记如图,A、B、C在⊙O上,则图中有哪几个圆周角?OBCA⌒若P为圆上异于B、C的一点,你能求出∠ BPC的度数吗?P1若连接OB,OC,那么∠ BOC为多少度?P2引入:二. 探索新知:OAB1、圆内接四边形,四边形外接圆如图,在圆上分别取A、B、C、D,
并顺次连接,这样我们得到一个四边形ABCD.我们把
四个顶点都在圆上的四边形叫做圆内接四边形,这个圆叫做四边形的外接圆。CD你能给圆内接多边形,多边形外接圆下一个定义吗?类比学习:二. 探索新知:2、想一想:(1)如图,四边形ABCD为⊙O的内接四边形,若∠B=80 ° ,你能求出∠ ADC的度数吗?(2)若∠B=70 ° ,
你能求出∠ ADC的度数吗?(3)若∠B=120 ° ,
你能求出∠ ADC的度数吗?(4)由此你能发现∠B与∠ ADC的关系吗? 你能证明你的猜想吗?二. 探索新知:3、试一试
(1)求下图中各个x、 y的值。(2)若四边形ABCD内接于⊙ O,且∠A:∠B:∠C=1:2:5,则∠D= 。三.应用新知:例1、如图, ⊙ C经过坐标原点,且与两坐标轴分别交于点A、B,点A的坐标为(0,4),M为圆上一点, ∠ BMO=135 ° ,求⊙ C的半径及点C的坐标.┒N例2、如图,AD是△ABC的外角∠ EAC的平分线,
AD与△ABC的外接圆交于点D。
求证:DB=DC.三.应用新知:三.应用新知:练习如图,AD是圆O的直径,BC=CD, ∠BAD=40 °,求∠B的度数。 这节课你在知识学习和探究方法方面有什么收获?四.课堂小结:还有哪些疑惑? 1、作业本(1) P22四.今天作业:2、课时作业本 P82---83五.拓展提高:课时作业本p83 第9题ABCD1、在同圆或等圆中,相等的圆周角所对的弧相等..O五.拓展提高:5、如图,AB是圆O的直径,CD⊥AB,垂足为E,若 ∠ACD=30 °,AE=2cm.求DB的长。你还有其它的解法吗?检测练习:2、 如图1,AB和CD都是⊙O的直径,∠AOC=50°,则∠C的度数是_____ .
3、如图2,已知CD为⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠C的度数是_____ .图1图225° 25° 检测练习:3、已知⊙O中弦AB的长等于半径,
求弦AB所对的圆心角和圆周角的度数。 圆心角为60度圆周角为 30 度或 150 度。变式:已知⊙O的弦AB将将圆周分成1:3的两条弧,求弦AB所对的圆心角和圆周角的度数。 检测练习:
同课章节目录
