2021-2022学年高一上学期数学人教A版(2019)必修第一册2.2基本不等式(第二课时)课件(16张ppt)
文档属性
| 名称 | 2021-2022学年高一上学期数学人教A版(2019)必修第一册2.2基本不等式(第二课时)课件(16张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 814.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 20:05:56 | ||
图片预览






文档简介
(共16张PPT)
第二章一元二次函数、方程和不等式
2.2 基本不等式
(第二课时)
1.进一步熟练掌握基本不等式,能够通过拼凑、变形等利用基本不等式求最值.
2.能够利用基本不等式解决实际问题.
通过学习掌握基本不等式及其应用,重点提升数学运算、逻辑推理、数学建模素养.
教学目标
素养要求
基本不等式:
基本不等式链:
复习引入:
例1:(1)用篱笆围成一个面积为100m2的矩形菜园,
问这个矩形的长、宽各为多少时,所用篱笆最短。
最短的篱笆是多少?
解:设矩形菜园的长为x m,宽为y m,
则xy=100,篱笆的长为2(x+y) m.
当且仅当x=y=10时,等号成立.
结论1:两个正变量积为定值,则和有最小值,当且仅当两值相等时取最值。
例题分析:
例1:(2)用一段长为36m的篱笆围成一个矩形菜园,
问这个矩形菜园的长和宽各为多少时,菜园的面
积最大,最大面积是多少?
解:设矩形菜园的长为x m,宽为y m,
当且仅当x=y=9时,等号成立.
则2(x + y)=36, x+y =18
菜园的面积为xy m2
结论2:两个正变量和为定值,则积有最大值,当且仅当两值相等时取最值。
例题分析:
若x、y为正数,则
(1)当x+y的值是常数S时,当且仅当x=y时,
xy有最大值_______;
(2)当xy的值是常数P时,当且仅当x=y时,
x+y有最小值_______。
①各项皆为正数;
②和为定值或积为定值;
③注意等号成立的条件。
一“正”
二“定”
三“相等”
和定积最大,积定和最小
用最值定理求最值的三个条件:
最值定理:
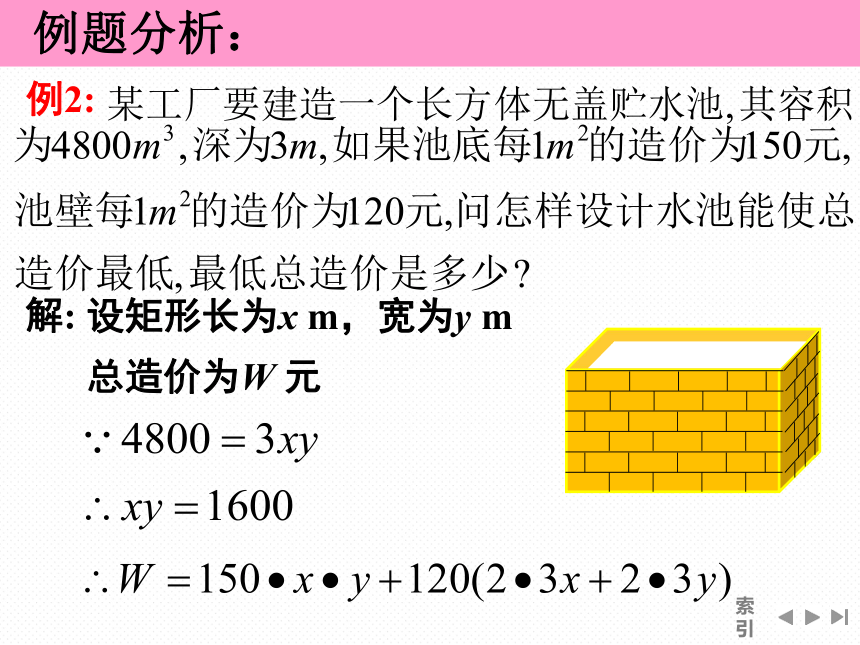
例2:
解:
设矩形长为x m,宽为y m
总造价为W 元
例题分析:
利用基本不等式解决实际问题的步骤,解实际问题时,首先审清题意,然后将实际问题转化为数学问题,再利用数学知识(函数及不等式性质等)解决问题.用基本不等式解决此类问题时,应按如下步骤进行:
(1)先理解题意,设变量.设变量时一般把要求最大值或最小值的变量定为函数.
(2)建立相应的函数关系式.把实际问题抽象为函数的最大值或最小值问题.
(3)在定义域内,求出函数的最大值或最小值.
(4)正确写出答案.
思维升华:
1、x>0,y>0,xy=16,求 x+2y 的最小值,
并说明此时x,y的值。
2、x>0,y>0,2x+3y=2,求 xy 的最大值,
并说明此时x,y的值。
课堂练习:
一正
二定
三相等
1、x>0,y>0,xy=16,求 x+2y 的最小值,
并说明此时x,y的值。
一正
二定
三相等
2、x>0,y>0,2x+3y=2,求 xy 的最大值,
并说明此时x,y的值。
3.(多选题)下列不等式正确的是( )
BC
4.已知正数a,b满足ab=10,则a+b的最小值是________.
50
5.已知m,n∈R,m2+n2=100,则mn的最大值是________.
解析 由m2+n2≥2mn,
1、两个重要的不等式:
(1)
(2)
(当且仅当a=b时,等号成立)
2、不等式的简单应用:主要在于求最值
把握“七字方针”即 “一正,二定,三相等”。
课堂小结:
第二章一元二次函数、方程和不等式
2.2 基本不等式
(第二课时)
1.进一步熟练掌握基本不等式,能够通过拼凑、变形等利用基本不等式求最值.
2.能够利用基本不等式解决实际问题.
通过学习掌握基本不等式及其应用,重点提升数学运算、逻辑推理、数学建模素养.
教学目标
素养要求
基本不等式:
基本不等式链:
复习引入:
例1:(1)用篱笆围成一个面积为100m2的矩形菜园,
问这个矩形的长、宽各为多少时,所用篱笆最短。
最短的篱笆是多少?
解:设矩形菜园的长为x m,宽为y m,
则xy=100,篱笆的长为2(x+y) m.
当且仅当x=y=10时,等号成立.
结论1:两个正变量积为定值,则和有最小值,当且仅当两值相等时取最值。
例题分析:
例1:(2)用一段长为36m的篱笆围成一个矩形菜园,
问这个矩形菜园的长和宽各为多少时,菜园的面
积最大,最大面积是多少?
解:设矩形菜园的长为x m,宽为y m,
当且仅当x=y=9时,等号成立.
则2(x + y)=36, x+y =18
菜园的面积为xy m2
结论2:两个正变量和为定值,则积有最大值,当且仅当两值相等时取最值。
例题分析:
若x、y为正数,则
(1)当x+y的值是常数S时,当且仅当x=y时,
xy有最大值_______;
(2)当xy的值是常数P时,当且仅当x=y时,
x+y有最小值_______。
①各项皆为正数;
②和为定值或积为定值;
③注意等号成立的条件。
一“正”
二“定”
三“相等”
和定积最大,积定和最小
用最值定理求最值的三个条件:
最值定理:
例2:
解:
设矩形长为x m,宽为y m
总造价为W 元
例题分析:
利用基本不等式解决实际问题的步骤,解实际问题时,首先审清题意,然后将实际问题转化为数学问题,再利用数学知识(函数及不等式性质等)解决问题.用基本不等式解决此类问题时,应按如下步骤进行:
(1)先理解题意,设变量.设变量时一般把要求最大值或最小值的变量定为函数.
(2)建立相应的函数关系式.把实际问题抽象为函数的最大值或最小值问题.
(3)在定义域内,求出函数的最大值或最小值.
(4)正确写出答案.
思维升华:
1、x>0,y>0,xy=16,求 x+2y 的最小值,
并说明此时x,y的值。
2、x>0,y>0,2x+3y=2,求 xy 的最大值,
并说明此时x,y的值。
课堂练习:
一正
二定
三相等
1、x>0,y>0,xy=16,求 x+2y 的最小值,
并说明此时x,y的值。
一正
二定
三相等
2、x>0,y>0,2x+3y=2,求 xy 的最大值,
并说明此时x,y的值。
3.(多选题)下列不等式正确的是( )
BC
4.已知正数a,b满足ab=10,则a+b的最小值是________.
50
5.已知m,n∈R,m2+n2=100,则mn的最大值是________.
解析 由m2+n2≥2mn,
1、两个重要的不等式:
(1)
(2)
(当且仅当a=b时,等号成立)
2、不等式的简单应用:主要在于求最值
把握“七字方针”即 “一正,二定,三相等”。
课堂小结:
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
