新人教版九年级上册24.2.2直线和圆的位置关系(第一课时)
文档属性
| 名称 | 新人教版九年级上册24.2.2直线和圆的位置关系(第一课时) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-26 00:00:00 | ||
图片预览









文档简介
课件52张PPT。 掌握直线与圆的位置关系的定义、性质及判定方法. 圆心到直线的距离是指过圆心向直线所作的垂线段的长度.注意数形结合思想的应用. 直线与圆位置关系的判定
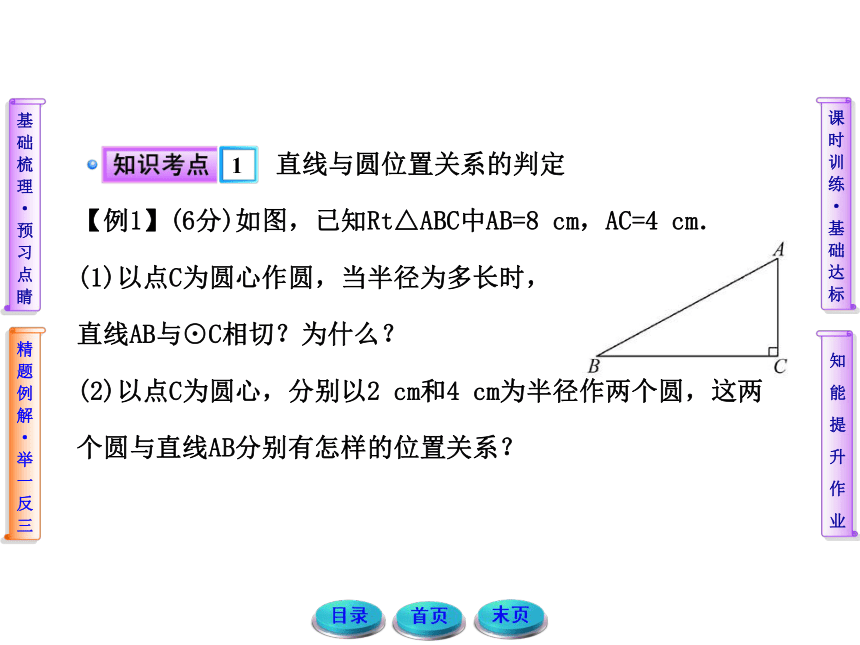
【例1】(6分)如图,已知Rt△ABC中AB=8 cm,AC=4 cm.
(1)以点C为圆心作圆,当半径为多长时,
直线AB与⊙C相切?为什么?
(2)以点C为圆心,分别以2 cm和4 cm为半径作两个圆,这两个圆与直线AB分别有怎样的位置关系?【规范解答】(1)如图,过点C作CD⊥AB,垂足为D.
在Rt△ABC中BC=
∴CD= …………………2分
因此,当半径为 cm时,AB与⊙C相切.
理由是:点C到AB的距离等于圆的半径,所以AB是⊙C的切
线. ………………………………………………………4分
(2)由(1)可知,圆心C到直线AB的距离d= cm,所以
当r=2时,d>r,⊙C与直线AB相离;……………………5分
当r=4时,d【解析】因为d>r,所以直线与圆相离.
答案:相离2.已知⊙O的半径为5,点P在直线l上,且OP=5,直线l与⊙O的位置关系是_____.
【解析】由题意知,点P在⊙O上,所以直线l与圆的公共点的个数为1或2,因此,直线与圆的位置关系是相切或相交.
答案:相切或相交3.在Rt△ABC中,∠C=90°,AC=3 cm,BC=4 cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?
(1)r=2 cm (2)r=2.4 cm (3)r=3 cm【解析】过点C作CD⊥AB于D在Rt△ABC中
根据三角形的面积公式有
AC·BC= AB·CD
即圆心C到AB的距离d=2.4 cm.
(1)当r=2 cm时,有d>r,因此⊙C和AB相离.
(2)当r=2.4 cm时,有d=r,因此⊙C和AB相切.
(3)当r=3 cm,有d<r,因此⊙O和AB相交. 经过圆外一点的直线与圆的位置关系有三种:相离、相切、相交;过圆上一点的直线与圆的位置关系为相切或相交;经过圆内一点的直线与圆的位置关系只有相交一种情况. 直线与圆位置关系的性质应用
【例2】如图,半径为2的⊙P,点P在直线y=2x-1上运动.
(1)当⊙P和x轴相切时,写出点P的坐标;
(2)当⊙P和y轴相切时,写出点P的坐标;
(3)⊙P是否能同时与x轴,y轴相切,若能,写出点P的坐标,若不能,说明理由.【思路点拨】 【自主解答】(1)⊙P与x轴相切时,点P的纵坐标应为2或-2.
y=2时,2x-1=2,x= ;
y=-2时,2x-1=-2,x=- ,∴P( ,2)或P(- ,-2).
(2)⊙P与y轴相切时,点P的横坐标应为2或-2,
x=2时,y=3;x=-2时,y=-5.
∴P(2,3)或P(-2,-5).
(3)不存在,因为⊙P与x轴、y轴同时相切时,|x|=|y|=2,不满足直线方程y=2x-1. 由直线与圆的位置关系推算d和r的关系有两种情形:一是已知d和位置关系求r;二是已知r和位置关系求d.解题的关键是准确把握位置关系与数量关系之间的对应.4.在Rt△ABC中,∠C=90°,AB=5,AC=3,以AB的中点为圆心的同心圆中,与BC,AC都相离的圆的半径应符合条件( )
(A)r>2 (B)r<2 (C)r<1.5 (D)r<1
【解析】选C.由勾股定理得,BC=4,所以AB的中点到BC、AC的距离分别为1.5、2,要使圆与BC,AC都相离,则r<1.5.5.(2010·西宁中考)如图,已知在直角坐标系中,半径为2的圆的圆心坐标为(3,-3),当该圆向上平移_____个单位时,它与x轴相切.【解析】由直线与圆相切判定d=r,得d=2,圆向上平移1个单位或5个单位.
答案:1或56.(2010 ·义乌中考)已知直线l与⊙O相切,若圆心O到直线l的距离是5,则⊙O的半径是_____.
【解析】直线与圆相切,则d=r.
答案:5 根据位置关系求d或r的值时,要特别注意相切的性质:d=r,同时注意直线与圆有公共点和线段与圆有公共点的区别与联系,防止漏解或错解. 1.(2010·青岛中考)如图,在Rt△ABC中,∠C = 90°,∠B = 30°,BC = 4 cm,以点C为圆心,以2 cm的长为半径作圆,则⊙C与AB的位置关系是( ).
(A)相离 (B)相切 (C)相交 (D)相切或相交
【解析】选B.过点C作CD⊥AB,因为∠B = 30°,所以CD=2cm=r,所以⊙C与AB相切.2.(2010·赤峰中考)如图,⊙O的圆心到直线l的距离为
3 cm,⊙O的半径为1 cm,将直线l向右(垂直于l的方向)平移,使l与⊙O相切,则平移的距离是( )
(A)1 cm (B)2 cm (C)4 cm (D)2 cm或4 cm【解析】选D.若直线与圆相切,则d=r.当圆在直线的右侧时,平移的距离为2 cm,当直线移动到圆的右侧且与圆相切时,平移的距离为4 cm.3.△ABC的面积为24 cm2,AC长8 cm,以B为圆心的圆与AC相切,则⊙B的半径为_____.
【解析】∵⊙B与AC相切.
∴⊙B的半径等于B点到AC的距离d.
由 AC×d=24得
d= =6(cm).
答案:6 cm4.如图,已知等腰梯形ABCD中,AD=3 cm,BC=11 cm,腰AB=5 cm,以A为圆心,AD为半径的⊙A与底边BC有怎样的位置关系?【解析】过A、D作AE⊥BC,DF⊥BC,垂足分别为E、F,由题
意知BE=CF=(BC-AD)÷2=4 (cm),
在Rt△ABE中,AE= =3(cm),又因为AD=3 cm,所
以以A为圆心,AD为半径的⊙A与底BC相切.一、选择题(每小题4分,共12分)
1.(2010·娄底中考)在平面直角坐标系中,以点(3,2)为圆心、3为半径的圆,一定( )
(A)与x轴相切,与y轴相切
(B)与x轴相切,与y轴相交
(C)与x轴相交,与y轴相切
(D)与x轴相交,与y轴相交 【解析】选C.点(3,2)到x轴的距离为2,小于半径,所以与x轴相交;到y轴的距离为 3,等于圆的半径,所以与y轴相切.2.在直角坐标系中,⊙O的半径为1,O为坐标原点,则直线
y=-x+ 与⊙O的位置关系是( )
(A)相离 (B)相交
(C)相切 (D)以上三种情形都有可能【解析】选C.如图,y=-x+ 与x轴交于点A( ,0),
与y轴交于点B(0, ),
则OA=OB= ,所以AB=2.
作OC⊥AB于点C.根据三角形面积公式知:
OA·OB=AB·OC,
即 × =2·OC,所以OC=1,
因为⊙O的半径为1,
所以直线y=-x+ 与⊙O相切.3.以点P(3,2 )为圆心的圆与x轴相切,则这个圆与y轴的位置关系是( )
(A) 相离 (B)相切 (C)相交 (D)相切或相交
【解析】选A.点P到x轴的距离为2 ,⊙P与x轴相切,所以
⊙P的半径是2 ,点P到y轴的距离为3,大于2 ,所以圆
与y轴相离.二、填空题(每小题4分,共12分)
4.(2010·潼南中考)如图,在矩形ABCD中,AB=6,BC=4,
⊙O是以AB为直径的圆,则直线DC与⊙O的位置关系是_____.【解析】由题意知,⊙O的半径为3,圆心到CD的距离等于4,所以⊙O与直线DC相离.
答案:相离5.已知⊙O的半径为R,直线AB与圆心O的距离为d,且方程
有实数根,则直线AB与⊙O的位置关系是____.
【解析】∵ 有实数根,
∴b2-4ac=4d-4R≥0,∴d≥R,
∴直线AB与⊙O相切或相离.
答案:相切或相离6.(2010·百色中考)如图,⊙O的直径
为20 cm,弦AB=16 cm,OD⊥AB,垂足为D.
则AB沿射线OD方向平移_____cm时可与
⊙O相切.
【解析】因为OD⊥AB,所以AD=8 cm,⊙O的直径为20 cm,所以OA=10 cm,在Rt△AOD中,根据勾股定理得OD=6 cm,所以当AB沿OD方向平移10-6=4 (cm)时,AB与圆相切.
答案:4 【归纳整合】此类题目在提供条件时,往往变换不同的方式,或联系一元二次方程,或联系图形面积求高,或联系勾股定理求高,最终目的是间接给出点到直线的距离,然后根据此距离与圆半径的关系确定直线与圆的位置关系.三、解答题(共26分)
7.(8分)如图,⊙P的半径为2,圆心
P在函数y= (x>0)的图象上运动,
(1)当⊙P与x轴相切时,求点P的坐标;
(2)当⊙P与坐标轴相离时,x满足的条
件是什么?【解析】(1)当⊙P与x轴相切时,即P点的纵坐标为2,代
入y= 得:x=3.
∴P点坐标为(3,2).
(2)当⊙P与坐标轴相离时,⊙P到x轴、y轴的距离都大于2.到y轴的距离大于2,此时x>2,
由(1)得,与x轴相离时,x<3,
∴当2此时P1E=1 cm,∴OP1=2 cm,∴PP1=6-2=4(cm),所用时间为4÷1=4 (s);
当⊙P在O的右侧与直线CD相切时,OP2=2 cm,
∴PP2=6+2=8(cm),所用时间为8÷1=8 (s).
当点P在P1P2(不包含点P1、P2)上时,d9.(10分)如图,据气象卫星显示,有
一股强热带风暴10小时后将在距A城正
东方向300千米的B城登陆,并陆续以
30千米/时的速度向西偏北30°的BN方向移动,风暴中心200
千米的范围内是受风暴影响的区域,试问A城是否会受这次
风暴的影响?如会,那么A城受台风影响的时间有多长?如
不会,请说明理由.( ≈2.65) 【解析】A城是否会受风暴的影响,取决
于风暴团在沿BN移动过程中,与以A为圆
心,200千米为半径的圆是否有交点,作
AE⊥BN于E.
∵∠ABN=30°,∴AE= AB=150(千米).
∵150<200,
∴A城要受这次风暴的影响,以A为圆心,200千米为半径作圆,交BN于C、D两点,则由勾股定理得:
DE= 千米,∴DC= 千米,
∴A城受台风影响的时间为:
≈8.83(小时).
【例1】(6分)如图,已知Rt△ABC中AB=8 cm,AC=4 cm.
(1)以点C为圆心作圆,当半径为多长时,
直线AB与⊙C相切?为什么?
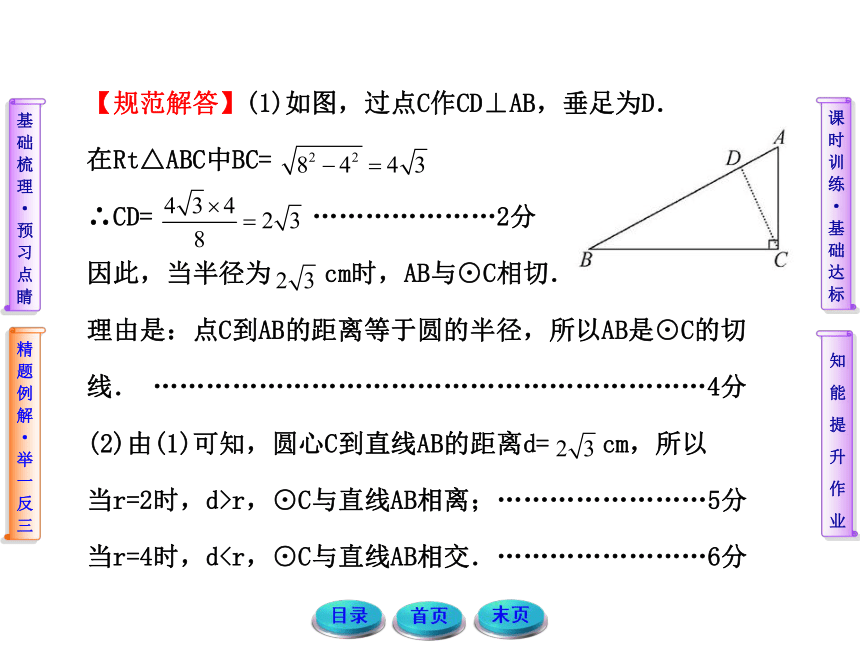
(2)以点C为圆心,分别以2 cm和4 cm为半径作两个圆,这两个圆与直线AB分别有怎样的位置关系?【规范解答】(1)如图,过点C作CD⊥AB,垂足为D.
在Rt△ABC中BC=
∴CD= …………………2分
因此,当半径为 cm时,AB与⊙C相切.
理由是:点C到AB的距离等于圆的半径,所以AB是⊙C的切
线. ………………………………………………………4分
(2)由(1)可知,圆心C到直线AB的距离d= cm,所以
当r=2时,d>r,⊙C与直线AB相离;……………………5分
当r=4时,d
答案:相离2.已知⊙O的半径为5,点P在直线l上,且OP=5,直线l与⊙O的位置关系是_____.
【解析】由题意知,点P在⊙O上,所以直线l与圆的公共点的个数为1或2,因此,直线与圆的位置关系是相切或相交.
答案:相切或相交3.在Rt△ABC中,∠C=90°,AC=3 cm,BC=4 cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?
(1)r=2 cm (2)r=2.4 cm (3)r=3 cm【解析】过点C作CD⊥AB于D在Rt△ABC中
根据三角形的面积公式有
AC·BC= AB·CD
即圆心C到AB的距离d=2.4 cm.
(1)当r=2 cm时,有d>r,因此⊙C和AB相离.
(2)当r=2.4 cm时,有d=r,因此⊙C和AB相切.
(3)当r=3 cm,有d<r,因此⊙O和AB相交. 经过圆外一点的直线与圆的位置关系有三种:相离、相切、相交;过圆上一点的直线与圆的位置关系为相切或相交;经过圆内一点的直线与圆的位置关系只有相交一种情况. 直线与圆位置关系的性质应用
【例2】如图,半径为2的⊙P,点P在直线y=2x-1上运动.
(1)当⊙P和x轴相切时,写出点P的坐标;
(2)当⊙P和y轴相切时,写出点P的坐标;
(3)⊙P是否能同时与x轴,y轴相切,若能,写出点P的坐标,若不能,说明理由.【思路点拨】 【自主解答】(1)⊙P与x轴相切时,点P的纵坐标应为2或-2.
y=2时,2x-1=2,x= ;
y=-2时,2x-1=-2,x=- ,∴P( ,2)或P(- ,-2).
(2)⊙P与y轴相切时,点P的横坐标应为2或-2,
x=2时,y=3;x=-2时,y=-5.
∴P(2,3)或P(-2,-5).
(3)不存在,因为⊙P与x轴、y轴同时相切时,|x|=|y|=2,不满足直线方程y=2x-1. 由直线与圆的位置关系推算d和r的关系有两种情形:一是已知d和位置关系求r;二是已知r和位置关系求d.解题的关键是准确把握位置关系与数量关系之间的对应.4.在Rt△ABC中,∠C=90°,AB=5,AC=3,以AB的中点为圆心的同心圆中,与BC,AC都相离的圆的半径应符合条件( )
(A)r>2 (B)r<2 (C)r<1.5 (D)r<1
【解析】选C.由勾股定理得,BC=4,所以AB的中点到BC、AC的距离分别为1.5、2,要使圆与BC,AC都相离,则r<1.5.5.(2010·西宁中考)如图,已知在直角坐标系中,半径为2的圆的圆心坐标为(3,-3),当该圆向上平移_____个单位时,它与x轴相切.【解析】由直线与圆相切判定d=r,得d=2,圆向上平移1个单位或5个单位.
答案:1或56.(2010 ·义乌中考)已知直线l与⊙O相切,若圆心O到直线l的距离是5,则⊙O的半径是_____.
【解析】直线与圆相切,则d=r.
答案:5 根据位置关系求d或r的值时,要特别注意相切的性质:d=r,同时注意直线与圆有公共点和线段与圆有公共点的区别与联系,防止漏解或错解. 1.(2010·青岛中考)如图,在Rt△ABC中,∠C = 90°,∠B = 30°,BC = 4 cm,以点C为圆心,以2 cm的长为半径作圆,则⊙C与AB的位置关系是( ).
(A)相离 (B)相切 (C)相交 (D)相切或相交
【解析】选B.过点C作CD⊥AB,因为∠B = 30°,所以CD=2cm=r,所以⊙C与AB相切.2.(2010·赤峰中考)如图,⊙O的圆心到直线l的距离为
3 cm,⊙O的半径为1 cm,将直线l向右(垂直于l的方向)平移,使l与⊙O相切,则平移的距离是( )
(A)1 cm (B)2 cm (C)4 cm (D)2 cm或4 cm【解析】选D.若直线与圆相切,则d=r.当圆在直线的右侧时,平移的距离为2 cm,当直线移动到圆的右侧且与圆相切时,平移的距离为4 cm.3.△ABC的面积为24 cm2,AC长8 cm,以B为圆心的圆与AC相切,则⊙B的半径为_____.
【解析】∵⊙B与AC相切.
∴⊙B的半径等于B点到AC的距离d.
由 AC×d=24得
d= =6(cm).
答案:6 cm4.如图,已知等腰梯形ABCD中,AD=3 cm,BC=11 cm,腰AB=5 cm,以A为圆心,AD为半径的⊙A与底边BC有怎样的位置关系?【解析】过A、D作AE⊥BC,DF⊥BC,垂足分别为E、F,由题
意知BE=CF=(BC-AD)÷2=4 (cm),
在Rt△ABE中,AE= =3(cm),又因为AD=3 cm,所
以以A为圆心,AD为半径的⊙A与底BC相切.一、选择题(每小题4分,共12分)
1.(2010·娄底中考)在平面直角坐标系中,以点(3,2)为圆心、3为半径的圆,一定( )
(A)与x轴相切,与y轴相切
(B)与x轴相切,与y轴相交
(C)与x轴相交,与y轴相切
(D)与x轴相交,与y轴相交 【解析】选C.点(3,2)到x轴的距离为2,小于半径,所以与x轴相交;到y轴的距离为 3,等于圆的半径,所以与y轴相切.2.在直角坐标系中,⊙O的半径为1,O为坐标原点,则直线
y=-x+ 与⊙O的位置关系是( )
(A)相离 (B)相交
(C)相切 (D)以上三种情形都有可能【解析】选C.如图,y=-x+ 与x轴交于点A( ,0),
与y轴交于点B(0, ),
则OA=OB= ,所以AB=2.
作OC⊥AB于点C.根据三角形面积公式知:
OA·OB=AB·OC,
即 × =2·OC,所以OC=1,
因为⊙O的半径为1,
所以直线y=-x+ 与⊙O相切.3.以点P(3,2 )为圆心的圆与x轴相切,则这个圆与y轴的位置关系是( )
(A) 相离 (B)相切 (C)相交 (D)相切或相交
【解析】选A.点P到x轴的距离为2 ,⊙P与x轴相切,所以
⊙P的半径是2 ,点P到y轴的距离为3,大于2 ,所以圆
与y轴相离.二、填空题(每小题4分,共12分)
4.(2010·潼南中考)如图,在矩形ABCD中,AB=6,BC=4,
⊙O是以AB为直径的圆,则直线DC与⊙O的位置关系是_____.【解析】由题意知,⊙O的半径为3,圆心到CD的距离等于4,所以⊙O与直线DC相离.
答案:相离5.已知⊙O的半径为R,直线AB与圆心O的距离为d,且方程
有实数根,则直线AB与⊙O的位置关系是____.
【解析】∵ 有实数根,
∴b2-4ac=4d-4R≥0,∴d≥R,
∴直线AB与⊙O相切或相离.
答案:相切或相离6.(2010·百色中考)如图,⊙O的直径
为20 cm,弦AB=16 cm,OD⊥AB,垂足为D.
则AB沿射线OD方向平移_____cm时可与
⊙O相切.
【解析】因为OD⊥AB,所以AD=8 cm,⊙O的直径为20 cm,所以OA=10 cm,在Rt△AOD中,根据勾股定理得OD=6 cm,所以当AB沿OD方向平移10-6=4 (cm)时,AB与圆相切.
答案:4 【归纳整合】此类题目在提供条件时,往往变换不同的方式,或联系一元二次方程,或联系图形面积求高,或联系勾股定理求高,最终目的是间接给出点到直线的距离,然后根据此距离与圆半径的关系确定直线与圆的位置关系.三、解答题(共26分)
7.(8分)如图,⊙P的半径为2,圆心
P在函数y= (x>0)的图象上运动,
(1)当⊙P与x轴相切时,求点P的坐标;
(2)当⊙P与坐标轴相离时,x满足的条
件是什么?【解析】(1)当⊙P与x轴相切时,即P点的纵坐标为2,代
入y= 得:x=3.
∴P点坐标为(3,2).
(2)当⊙P与坐标轴相离时,⊙P到x轴、y轴的距离都大于2.到y轴的距离大于2,此时x>2,
由(1)得,与x轴相离时,x<3,
∴当2
当⊙P在O的右侧与直线CD相切时,OP2=2 cm,
∴PP2=6+2=8(cm),所用时间为8÷1=8 (s).
当点P在P1P2(不包含点P1、P2)上时,d
一股强热带风暴10小时后将在距A城正
东方向300千米的B城登陆,并陆续以
30千米/时的速度向西偏北30°的BN方向移动,风暴中心200
千米的范围内是受风暴影响的区域,试问A城是否会受这次
风暴的影响?如会,那么A城受台风影响的时间有多长?如
不会,请说明理由.( ≈2.65) 【解析】A城是否会受风暴的影响,取决
于风暴团在沿BN移动过程中,与以A为圆
心,200千米为半径的圆是否有交点,作
AE⊥BN于E.
∵∠ABN=30°,∴AE= AB=150(千米).
∵150<200,
∴A城要受这次风暴的影响,以A为圆心,200千米为半径作圆,交BN于C、D两点,则由勾股定理得:
DE= 千米,∴DC= 千米,
∴A城受台风影响的时间为:
≈8.83(小时).
同课章节目录
