新人教版九年级上册24.2.2直线和圆的位置关系(第二课时)
文档属性
| 名称 | 新人教版九年级上册24.2.2直线和圆的位置关系(第二课时) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-26 22:40:56 | ||
图片预览







文档简介
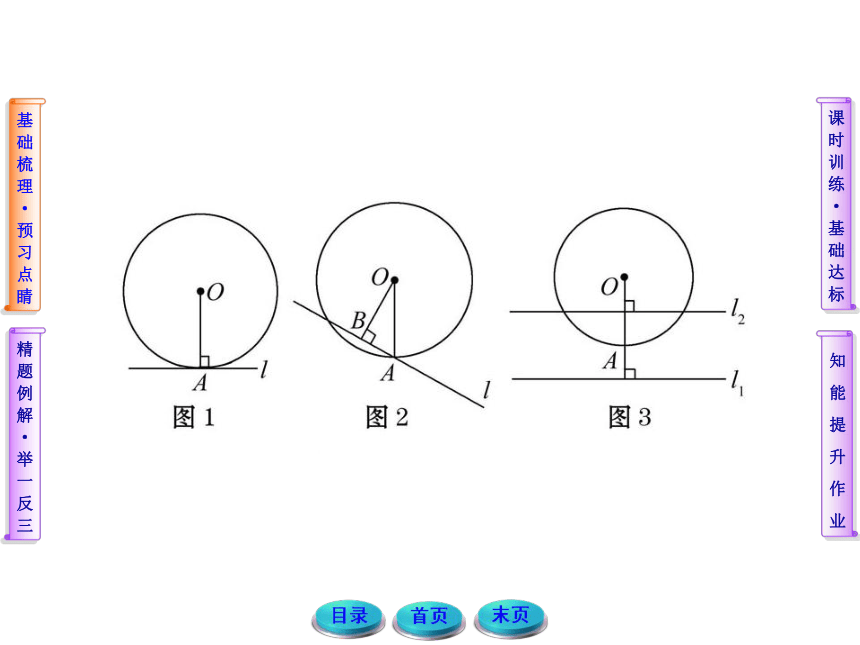
课件58张PPT。 掌握切线的判定方法,并能运用其判断直线是圆的切线. 结合切线的定义理解:“圆心到直线的距离等于圆的半径”等价于“经过半径的外端且垂直于半径”. 切线的判定
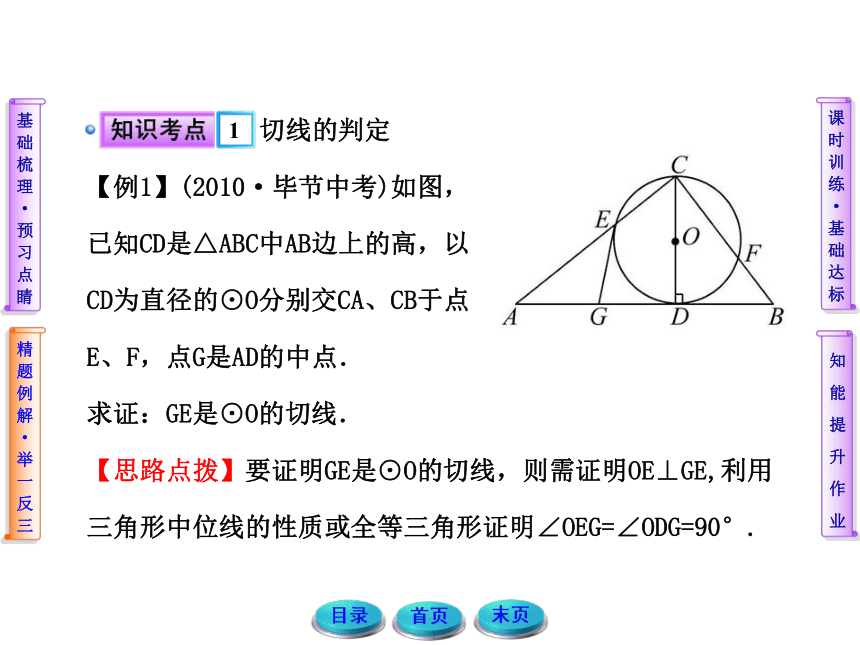
【例1】(2010·毕节中考)如图,
已知CD是△ABC中AB边上的高,以
CD为直径的⊙O分别交CA、CB于点
E、F,点G是AD的中点.
求证:GE是⊙O的切线.
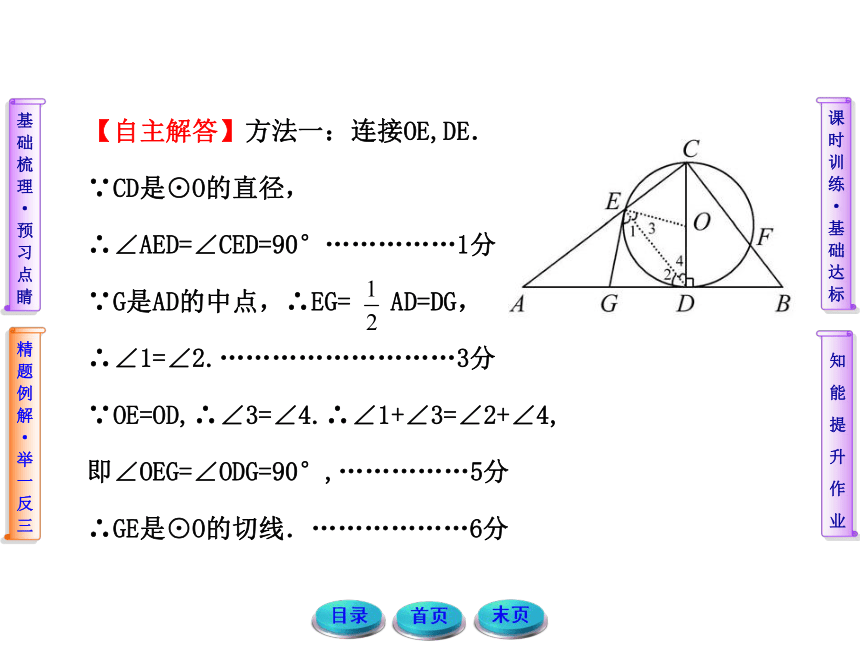
【思路点拨】要证明GE是⊙O的切线,则需证明OE⊥GE,利用三角形中位线的性质或全等三角形证明∠OEG=∠ODG=90°.【自主解答】方法一:连接OE,DE.
∵CD是⊙O的直径,
∴∠AED=∠CED=90°……………1分
∵G是AD的中点,∴EG= AD=DG,
∴∠1=∠2.………………………3分
∵OE=OD,∴∠3=∠4.∴∠1+∠3=∠2+∠4,
即∠OEG=∠ODG=90°,……………5分
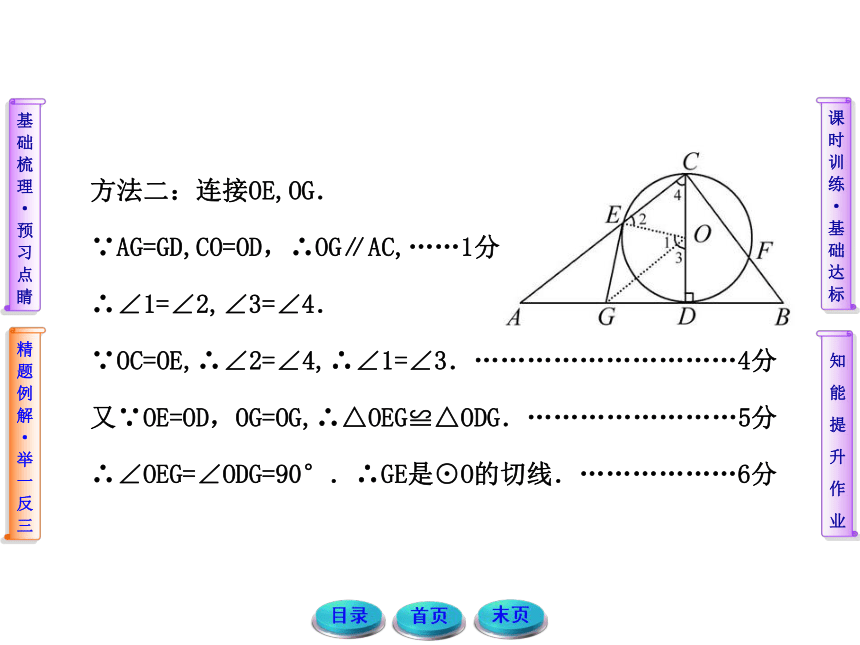
∴GE是⊙O的切线.………………6分 方法二:连接OE,OG.
∵AG=GD,CO=OD,∴OG∥AC,……1分
∴∠1=∠2,∠3=∠4.
∵OC=OE,∴∠2=∠4,∴∠1=∠3.…………………………4分
又∵OE=OD,OG=OG,∴△OEG≌△ODG.……………………5分
∴∠OEG=∠ODG=90°.∴GE是⊙O的切线.………………6分 应用切线的判定定理证明直线与圆相切时,常用的辅助线的作法为:
(1)若已知直线与圆有公共点,则连接圆心与公共点,证明垂直,即“连半径,证垂直”;
(2)若直线与圆的公共点没有确定,则过圆心作直线的垂线,证明圆心到直线的距离等于圆的半径,即“作垂直,证等径”.1.下列说法正确的是( )
(A)与圆有公共点的直线是圆的切线
(B)到圆心的距离等于圆的半径的直线是圆的切线
(C)垂直于圆的半径的直线是圆的切线
(D)过圆的半径外端的直线是圆的切线
【解析】选B.根据切线的定义,只需满足直线与圆有惟一的公共点;根据切线的判定,“经过半径外端”和“与半径垂直”二者缺一不可,故选B.2.已知:如图,在△ABC中,AB=AC,
以AB为直径的⊙O交BC于点D,过点D
作DE⊥AC交AC于点E.
求证:DE是⊙O的切线.
【证明】连接OD,则OD=OB,
∴∠B=∠BDO.
∵AB=AC,∴∠B=∠C,∴∠BDO=∠C,∴OD∥AC,∴∠ODE=∠DEC.
∵DE⊥AC,∴∠DEC=90°,∴∠ODE=90°,即DE⊥OD,∴DE是⊙O的切线. 切线的三种判定方法:①和圆只有一个公共点的直线是圆的切线;
②到圆心的距离等于圆的半径的直线是圆的切线;
③经过半径的外端且垂直于这条半径的直线是圆的切线. 切线的性质
【例2】(2010·济南中考)如图,AB是⊙O的
切线,A为切点,AC是⊙O的弦,过O作OH⊥AC
交AC于点H.若OH=2,AB=12,BO=13.
求:(1)⊙O的半径;(2)AC的值.【思路点拨】 【自主解答】(1)∵AB是⊙O的切线,A为切点,∴OA⊥AB.在
Rt△AOB中,AO= =5,∴⊙O的半径为5.
(2)∵OH⊥AC,在Rt△AOH中,AH=
又∵OH⊥AC,∴AC=2AH= 切线性质定理的应用,一般是连接切点与圆心,构造垂直关系,利用垂直关系进行证明或计算,有时也涉及到勾股定理的应用. 3.(2010·珠海中考)如图,PA、PB是
⊙O的切线,切点分别是A、B,如果
∠P=60°,那么∠AOB等于( )
(A)60° (B)90° (C)120° (D)150°【解析】选C.因为PA、PB是⊙O的切线,切点分别是A、B,连接OA、OB,则∠OAP=∠OBP=90°,又∠P=60°,所以∠AOB=120°.4.(2010·温州中考)如图,在△ABC中,AB=BC=2,以AB为直径的⊙O与BC相切于点B,则AC等于( )
【解析】选C.因为BC与⊙O相切,所以AB⊥BC,
所以 已知切线,应用切线的性质构造垂直关系进行证明或使用90°角进行相关计算时,应注意切线的性质有如下几个:①切线和圆只有一个公共点;②圆心到切线的距离等于圆的半径;③切线垂直于过切点的半径;④经过圆心且垂直于切线的直线必经过切点;⑤经过切点且垂直于切线的直线必经过圆心.应用时要注意性质与判定的区别. 1.如图,AB为⊙O的直径,C为⊙O上一点,DA和过点C的切线互相垂直,垂足为点D,若∠CBA=55°,则∠CAD的度数为
( )
(A)70° (B)35° (C)45° (D)60°【解析】选B.连接OC,∵CD是⊙O的切线,∴OC⊥CD,
又∵AD⊥CD,∴OC∥AD,∴∠ACO=∠CAD,又∵OA=OC,∴∠CAO=∠ACO,∴∠CAD=∠CAO.∵AB为⊙O的直径,∴∠ACB=90°,且∠CBA=55°,∴∠CAO=35°,
∴∠CAD=35°.2.(2010·眉山中考)下列命题中,真命题是( )
(A)对角线互相垂直且相等的四边形是正方形
(B)等腰梯形既是轴对称图形又是中心对称图形
(C)圆的切线垂直于经过切点的半径
(D)垂直于同一直线的两条直线互相垂直
【解析】选C.依据切线的性质判断.3.如图,点B是⊙O上一点,AO=6 cm,
AB= cm,且⊙O的半径为4 cm,则直
线AB与⊙O的位置关系是_____.
【解析】连接OB.因为AO2=AB2+BO2,所以∠ABO=90°,所以AB与⊙O相切.
答案:相切4.(2010·徐州中考)如图,在以O为圆心
的两个同心圆中,大圆的弦AB与小圆相
切于点C,若大圆的半径为5 cm,小圆的
半径为3 cm,则弦AB的长为_____cm.【解析】连接OC、OA.
∵AB切小圆于C,∴OC⊥AB,
∴AC=BC.
在Rt△OAC中,
= =4(cm).
∴AB=2AC=2×4=8(cm).
答案:85.已知:如图,AB是⊙O的直径,BC和⊙O相切于点B,⊙O的弦AD平行于OC.
求证:DC是⊙O的切线.【证明】如图,连接OD.
∵AD∥OC,∴∠1=∠A,∠2=∠3.
又∵∠3=∠A,∴∠1=∠2.
又∵OD=OB,OC=OC,
∴△BOC≌△DOC,
∴∠ODC=∠OBC=90°,∴OD⊥DC,即DC切⊙O于D,DC是⊙O的切线.一、选择题(每小题4分,共12分)
1.如图,AB是⊙O的直径,BC是⊙O的切线,
AC交⊙O于点D,AB=6,BC=8,则BD的长为
( )
(A)4 (B)4.8
(C)5.2 (D)6【解析】选B.∵BC是⊙O的切线,∴AB⊥BC,
∴ ,又∵AB是⊙O的直径,
∴BD⊥AC,∴AB·BC=AC·BD,解得BD=4.8.2.(2010·三明中考)如图,在平面
直角坐标系中,点P在第一象限,⊙P
与x轴相切于点Q,与y轴交于两点
M(0,2),N(0,8),则点P的坐标
是( )
(A)(5,3) (B)(3,5)
(C)(5,4) (D)(4,5)【解析】选D.如图,连接PQ、PM,过点P作
PA⊥MN,垂足为A,则MA=NA=3,∵⊙P与x轴
相切,∴PQ⊥OQ,
∴PQ=OA=5,在Rt△APM中,根据勾股定理可得AP=4,∴点P的坐标为(4,5). 3.如图,AB是⊙O的直径,⊙O交BC的中点
于D,DE⊥AC于E,连接AD,则下列结论中
正确的个数是( )
①AD⊥BC;②∠EDA=∠B;
③OA= AC;④DE是⊙O的切线.
(A)1个 (B)2个 (C)3个 (D)4个【解析】选D.∵AB为⊙O的直径,∴∠ADB=90°,
故①正确.
连接OD.∵D为BC的中点,O为AB的中点,∴OD∥AC,∴∠C=∠ODB=∠B,
∴AB=AC,即OA= AC,故③正确.
又∵DE⊥AC,∴OD⊥DE,
∴DE是⊙O的切线,故④正确.
又∵∠EDA+∠ADO=90°,∠DAB+∠B=90°,
∠OAD=∠ODA,∴∠EDA=∠B,故②正确.二、填空题(每小题4分,共12分)
4.如图所示,AB为⊙O的直径,点P为AB
延长线上的一个动点,过点P作⊙O的切
线,切点为C,连接AC,∠CPA的平分线交
AC于点M,则∠CMP的度数为_____.【解析】连接OC,∵PC为⊙O的切线,
∴∠OCP=90°,∠CMP=∠A+∠APM
∵OA=OC,∴∠COP=2∠A,
即∠A= ∠COP.
又∵PM平分∠APC,∴∠APM= ∠APC.
∴∠CMP= ∠COP+ ∠APC
= (∠COP+∠APC)= ×90°=45°
答案:45°5.如图,PT切⊙O于点T,经过圆心的割
线PAB交⊙O于点A、B,已知PT=4,PA=2,
则⊙O的直径为_____.
【解析】连接OT,则OT⊥PT.在Rt△PTO中,设圆的半径为R,则OP2=OT2+PT2,即(R+2)2=R2+42,解得R=3,所以⊙O的直径为6.
答案:66.如图,∠ABC=90°,O为射线BC上一点,以点O为圆心、BO的一半长为半径作⊙O,当射线BA绕点B按顺时针方向旋转度_____时,与⊙O相切.【解析】分情况讨论:
(1)如图①,设BA经旋转与⊙O切于点P,连接OP,则
OP⊥BP,
又∵OP= OB,
∴∠OBP=30°,∴∠ABP=60°.
(2)如图②,同理可求得
∠OBP′=30°,∴∠ABP′=120°.
答案:60或120三、解答题(共26分)
7.(8分)(2010·赤峰中考)如图,AB是
⊙O的直径,BC是一条弦,连接OC并延长OC
至P点,并使PC=BC,∠BOC=60°.
(1)求证:PB是⊙O的切线;
(2)若⊙O的半径长为1,且AB、PB的长是一元二次方程x2+bx+c=0的两个根,求b、c的值.【解析】(1)在△BOC中,∵OB=OC,∠BOC=60°,
∴∠OBC=∠OCB=∠BOC=60°.
又∵PC=BC,∴∠CBP=∠CPB= ∠OCB=30°,
∴∠OBP=∠OBC+∠CBP=60°+30°=90°,
∴PB⊥AB.又∵AB是直径,∴PB是⊙O的切线.(2)∵OB=1,∴AB=2.
在Rt△POB中,∠CBP=30°,∴OP=2,
由勾股定理得,PB= .
设x2+bx+c=0的两个根分别为x1,x2,
由题意知,x1=2,x2= ,
∴x1+x2=2+ ,x1·x2= ,
∴b=-(2+ ),c= .8.(8分)(2010·临沂中考)如图,AB是半圆的直径,O为圆心,AD、BD是半圆的弦,且∠PDA=∠PBD.
(1)判断直线PD是否为⊙O的切线,并说明理由;
(2)如果∠BDE=60°,PD= ,求PA的长.【解析】(1)PD是⊙O的切线.
连接OD,∵OB=OD,
∴∠2=∠PBD.
又∵∠PDA=∠PBD.
∴∠PDA=∠2.
又∵AB是半圆的直径,∴∠ADB=90°,
即∠1+∠2=90°,∴∠1+∠PDA=90°,
即OD⊥PD.∴PD是⊙O的切线.(2)∵∠BDE=60°,∠ODE=90°,∠ADB=90°,
∴∠2=30°,∠1=60°.
∵OA=OD,∴△AOD是等边三角形.
∴∠POD=60°.∴∠P=∠PDA=30°.
在Rt△PDO中,设OD=x,∴x2+( )2=(2x)2,
∴x1=1,x2=-1(不合题意,舍去),∴PA=1. 【归纳整合】在中考中,切线的性质及判定往往结合在一起进行考查,应先判定直线与圆的位置关系,再利用位置关系解题.在应用中要切实注意性质与判定的区别:切线的判定定理是在未知相切而要证明相切的情况下使用,性质定理是在已知相切而要推出其他的结论时使用.【拓展延伸】
9.(10分)(1)如图(1)所示,OA、OB是⊙O的两条半径,且OA⊥OB,点C是OB延长线上任意的一点,过点C作CD切⊙O于点D,连接AD交OC于点E,
求证:CD=CE.
(2)若将图(1)中的半径OB所在的直线向上平行移动交OA于点F,交⊙O于点B′,其他条件不变,如图(2),那么上述结论CD=CE还成立吗?为什么?(3)若将图(1)中的半径OB所在的直线向上平行移动到⊙O外的CF,点E是DA延长线与CF的交点,其他条件不变,如图(3),那么上述结论CD=CE还成立吗?为什么?【解析】(1)连接OD,则OD⊥CD,
∴∠CDE+∠ODA=90°.
在Rt△AOE中,∠AEO+∠A=90°.
在⊙O中,∵OA=OD,∴∠A=∠ODA,
∴∠AEO=∠CDE,又∵∠AEO=∠CED,
∴∠CDE=∠CED,∴CD=CE.(2)CE=CD仍然成立.连接OD,在Rt△AFE中,
∠A+∠AEF=90°.
∵∠ADO+∠CDE=90°,又∵OA=OD,
∴∠A=∠ADO,∴∠AEF=∠CDE.
又∵∠AEF=∠DEC,
∴∠DEC=∠CDE,∴CE=CD.(3)CE=CD仍然成立.连接OD,
∠ODA+∠ADC=90°,在Rt△EAG中,
∠CEA+∠EAG=90°.又∵OA=OD,
∴∠OAD=∠ODA,∴∠OAD+∠ADC=90°.
又∵∠EAG=∠OAD,∴∠CEA=∠CDA,
∴CE=CD.谢谢
【例1】(2010·毕节中考)如图,
已知CD是△ABC中AB边上的高,以
CD为直径的⊙O分别交CA、CB于点
E、F,点G是AD的中点.
求证:GE是⊙O的切线.
【思路点拨】要证明GE是⊙O的切线,则需证明OE⊥GE,利用三角形中位线的性质或全等三角形证明∠OEG=∠ODG=90°.【自主解答】方法一:连接OE,DE.
∵CD是⊙O的直径,
∴∠AED=∠CED=90°……………1分
∵G是AD的中点,∴EG= AD=DG,
∴∠1=∠2.………………………3分
∵OE=OD,∴∠3=∠4.∴∠1+∠3=∠2+∠4,
即∠OEG=∠ODG=90°,……………5分
∴GE是⊙O的切线.………………6分 方法二:连接OE,OG.
∵AG=GD,CO=OD,∴OG∥AC,……1分
∴∠1=∠2,∠3=∠4.
∵OC=OE,∴∠2=∠4,∴∠1=∠3.…………………………4分
又∵OE=OD,OG=OG,∴△OEG≌△ODG.……………………5分
∴∠OEG=∠ODG=90°.∴GE是⊙O的切线.………………6分 应用切线的判定定理证明直线与圆相切时,常用的辅助线的作法为:
(1)若已知直线与圆有公共点,则连接圆心与公共点,证明垂直,即“连半径,证垂直”;
(2)若直线与圆的公共点没有确定,则过圆心作直线的垂线,证明圆心到直线的距离等于圆的半径,即“作垂直,证等径”.1.下列说法正确的是( )
(A)与圆有公共点的直线是圆的切线
(B)到圆心的距离等于圆的半径的直线是圆的切线
(C)垂直于圆的半径的直线是圆的切线
(D)过圆的半径外端的直线是圆的切线
【解析】选B.根据切线的定义,只需满足直线与圆有惟一的公共点;根据切线的判定,“经过半径外端”和“与半径垂直”二者缺一不可,故选B.2.已知:如图,在△ABC中,AB=AC,
以AB为直径的⊙O交BC于点D,过点D
作DE⊥AC交AC于点E.
求证:DE是⊙O的切线.
【证明】连接OD,则OD=OB,
∴∠B=∠BDO.
∵AB=AC,∴∠B=∠C,∴∠BDO=∠C,∴OD∥AC,∴∠ODE=∠DEC.
∵DE⊥AC,∴∠DEC=90°,∴∠ODE=90°,即DE⊥OD,∴DE是⊙O的切线. 切线的三种判定方法:①和圆只有一个公共点的直线是圆的切线;
②到圆心的距离等于圆的半径的直线是圆的切线;
③经过半径的外端且垂直于这条半径的直线是圆的切线. 切线的性质
【例2】(2010·济南中考)如图,AB是⊙O的
切线,A为切点,AC是⊙O的弦,过O作OH⊥AC
交AC于点H.若OH=2,AB=12,BO=13.
求:(1)⊙O的半径;(2)AC的值.【思路点拨】 【自主解答】(1)∵AB是⊙O的切线,A为切点,∴OA⊥AB.在
Rt△AOB中,AO= =5,∴⊙O的半径为5.
(2)∵OH⊥AC,在Rt△AOH中,AH=
又∵OH⊥AC,∴AC=2AH= 切线性质定理的应用,一般是连接切点与圆心,构造垂直关系,利用垂直关系进行证明或计算,有时也涉及到勾股定理的应用. 3.(2010·珠海中考)如图,PA、PB是
⊙O的切线,切点分别是A、B,如果
∠P=60°,那么∠AOB等于( )
(A)60° (B)90° (C)120° (D)150°【解析】选C.因为PA、PB是⊙O的切线,切点分别是A、B,连接OA、OB,则∠OAP=∠OBP=90°,又∠P=60°,所以∠AOB=120°.4.(2010·温州中考)如图,在△ABC中,AB=BC=2,以AB为直径的⊙O与BC相切于点B,则AC等于( )
【解析】选C.因为BC与⊙O相切,所以AB⊥BC,
所以 已知切线,应用切线的性质构造垂直关系进行证明或使用90°角进行相关计算时,应注意切线的性质有如下几个:①切线和圆只有一个公共点;②圆心到切线的距离等于圆的半径;③切线垂直于过切点的半径;④经过圆心且垂直于切线的直线必经过切点;⑤经过切点且垂直于切线的直线必经过圆心.应用时要注意性质与判定的区别. 1.如图,AB为⊙O的直径,C为⊙O上一点,DA和过点C的切线互相垂直,垂足为点D,若∠CBA=55°,则∠CAD的度数为
( )
(A)70° (B)35° (C)45° (D)60°【解析】选B.连接OC,∵CD是⊙O的切线,∴OC⊥CD,
又∵AD⊥CD,∴OC∥AD,∴∠ACO=∠CAD,又∵OA=OC,∴∠CAO=∠ACO,∴∠CAD=∠CAO.∵AB为⊙O的直径,∴∠ACB=90°,且∠CBA=55°,∴∠CAO=35°,
∴∠CAD=35°.2.(2010·眉山中考)下列命题中,真命题是( )
(A)对角线互相垂直且相等的四边形是正方形
(B)等腰梯形既是轴对称图形又是中心对称图形
(C)圆的切线垂直于经过切点的半径
(D)垂直于同一直线的两条直线互相垂直
【解析】选C.依据切线的性质判断.3.如图,点B是⊙O上一点,AO=6 cm,
AB= cm,且⊙O的半径为4 cm,则直
线AB与⊙O的位置关系是_____.
【解析】连接OB.因为AO2=AB2+BO2,所以∠ABO=90°,所以AB与⊙O相切.
答案:相切4.(2010·徐州中考)如图,在以O为圆心
的两个同心圆中,大圆的弦AB与小圆相
切于点C,若大圆的半径为5 cm,小圆的
半径为3 cm,则弦AB的长为_____cm.【解析】连接OC、OA.
∵AB切小圆于C,∴OC⊥AB,
∴AC=BC.
在Rt△OAC中,
= =4(cm).
∴AB=2AC=2×4=8(cm).
答案:85.已知:如图,AB是⊙O的直径,BC和⊙O相切于点B,⊙O的弦AD平行于OC.
求证:DC是⊙O的切线.【证明】如图,连接OD.
∵AD∥OC,∴∠1=∠A,∠2=∠3.
又∵∠3=∠A,∴∠1=∠2.
又∵OD=OB,OC=OC,
∴△BOC≌△DOC,
∴∠ODC=∠OBC=90°,∴OD⊥DC,即DC切⊙O于D,DC是⊙O的切线.一、选择题(每小题4分,共12分)
1.如图,AB是⊙O的直径,BC是⊙O的切线,
AC交⊙O于点D,AB=6,BC=8,则BD的长为
( )
(A)4 (B)4.8
(C)5.2 (D)6【解析】选B.∵BC是⊙O的切线,∴AB⊥BC,
∴ ,又∵AB是⊙O的直径,
∴BD⊥AC,∴AB·BC=AC·BD,解得BD=4.8.2.(2010·三明中考)如图,在平面
直角坐标系中,点P在第一象限,⊙P
与x轴相切于点Q,与y轴交于两点
M(0,2),N(0,8),则点P的坐标
是( )
(A)(5,3) (B)(3,5)
(C)(5,4) (D)(4,5)【解析】选D.如图,连接PQ、PM,过点P作
PA⊥MN,垂足为A,则MA=NA=3,∵⊙P与x轴
相切,∴PQ⊥OQ,
∴PQ=OA=5,在Rt△APM中,根据勾股定理可得AP=4,∴点P的坐标为(4,5). 3.如图,AB是⊙O的直径,⊙O交BC的中点
于D,DE⊥AC于E,连接AD,则下列结论中
正确的个数是( )
①AD⊥BC;②∠EDA=∠B;
③OA= AC;④DE是⊙O的切线.
(A)1个 (B)2个 (C)3个 (D)4个【解析】选D.∵AB为⊙O的直径,∴∠ADB=90°,
故①正确.
连接OD.∵D为BC的中点,O为AB的中点,∴OD∥AC,∴∠C=∠ODB=∠B,
∴AB=AC,即OA= AC,故③正确.
又∵DE⊥AC,∴OD⊥DE,
∴DE是⊙O的切线,故④正确.
又∵∠EDA+∠ADO=90°,∠DAB+∠B=90°,
∠OAD=∠ODA,∴∠EDA=∠B,故②正确.二、填空题(每小题4分,共12分)
4.如图所示,AB为⊙O的直径,点P为AB
延长线上的一个动点,过点P作⊙O的切
线,切点为C,连接AC,∠CPA的平分线交
AC于点M,则∠CMP的度数为_____.【解析】连接OC,∵PC为⊙O的切线,
∴∠OCP=90°,∠CMP=∠A+∠APM
∵OA=OC,∴∠COP=2∠A,
即∠A= ∠COP.
又∵PM平分∠APC,∴∠APM= ∠APC.
∴∠CMP= ∠COP+ ∠APC
= (∠COP+∠APC)= ×90°=45°
答案:45°5.如图,PT切⊙O于点T,经过圆心的割
线PAB交⊙O于点A、B,已知PT=4,PA=2,
则⊙O的直径为_____.
【解析】连接OT,则OT⊥PT.在Rt△PTO中,设圆的半径为R,则OP2=OT2+PT2,即(R+2)2=R2+42,解得R=3,所以⊙O的直径为6.
答案:66.如图,∠ABC=90°,O为射线BC上一点,以点O为圆心、BO的一半长为半径作⊙O,当射线BA绕点B按顺时针方向旋转度_____时,与⊙O相切.【解析】分情况讨论:
(1)如图①,设BA经旋转与⊙O切于点P,连接OP,则
OP⊥BP,
又∵OP= OB,
∴∠OBP=30°,∴∠ABP=60°.
(2)如图②,同理可求得
∠OBP′=30°,∴∠ABP′=120°.
答案:60或120三、解答题(共26分)
7.(8分)(2010·赤峰中考)如图,AB是
⊙O的直径,BC是一条弦,连接OC并延长OC
至P点,并使PC=BC,∠BOC=60°.
(1)求证:PB是⊙O的切线;
(2)若⊙O的半径长为1,且AB、PB的长是一元二次方程x2+bx+c=0的两个根,求b、c的值.【解析】(1)在△BOC中,∵OB=OC,∠BOC=60°,
∴∠OBC=∠OCB=∠BOC=60°.
又∵PC=BC,∴∠CBP=∠CPB= ∠OCB=30°,
∴∠OBP=∠OBC+∠CBP=60°+30°=90°,
∴PB⊥AB.又∵AB是直径,∴PB是⊙O的切线.(2)∵OB=1,∴AB=2.
在Rt△POB中,∠CBP=30°,∴OP=2,
由勾股定理得,PB= .
设x2+bx+c=0的两个根分别为x1,x2,
由题意知,x1=2,x2= ,
∴x1+x2=2+ ,x1·x2= ,
∴b=-(2+ ),c= .8.(8分)(2010·临沂中考)如图,AB是半圆的直径,O为圆心,AD、BD是半圆的弦,且∠PDA=∠PBD.
(1)判断直线PD是否为⊙O的切线,并说明理由;
(2)如果∠BDE=60°,PD= ,求PA的长.【解析】(1)PD是⊙O的切线.
连接OD,∵OB=OD,
∴∠2=∠PBD.
又∵∠PDA=∠PBD.
∴∠PDA=∠2.
又∵AB是半圆的直径,∴∠ADB=90°,
即∠1+∠2=90°,∴∠1+∠PDA=90°,
即OD⊥PD.∴PD是⊙O的切线.(2)∵∠BDE=60°,∠ODE=90°,∠ADB=90°,
∴∠2=30°,∠1=60°.
∵OA=OD,∴△AOD是等边三角形.
∴∠POD=60°.∴∠P=∠PDA=30°.
在Rt△PDO中,设OD=x,∴x2+( )2=(2x)2,
∴x1=1,x2=-1(不合题意,舍去),∴PA=1. 【归纳整合】在中考中,切线的性质及判定往往结合在一起进行考查,应先判定直线与圆的位置关系,再利用位置关系解题.在应用中要切实注意性质与判定的区别:切线的判定定理是在未知相切而要证明相切的情况下使用,性质定理是在已知相切而要推出其他的结论时使用.【拓展延伸】
9.(10分)(1)如图(1)所示,OA、OB是⊙O的两条半径,且OA⊥OB,点C是OB延长线上任意的一点,过点C作CD切⊙O于点D,连接AD交OC于点E,
求证:CD=CE.
(2)若将图(1)中的半径OB所在的直线向上平行移动交OA于点F,交⊙O于点B′,其他条件不变,如图(2),那么上述结论CD=CE还成立吗?为什么?(3)若将图(1)中的半径OB所在的直线向上平行移动到⊙O外的CF,点E是DA延长线与CF的交点,其他条件不变,如图(3),那么上述结论CD=CE还成立吗?为什么?【解析】(1)连接OD,则OD⊥CD,
∴∠CDE+∠ODA=90°.
在Rt△AOE中,∠AEO+∠A=90°.
在⊙O中,∵OA=OD,∴∠A=∠ODA,
∴∠AEO=∠CDE,又∵∠AEO=∠CED,
∴∠CDE=∠CED,∴CD=CE.(2)CE=CD仍然成立.连接OD,在Rt△AFE中,
∠A+∠AEF=90°.
∵∠ADO+∠CDE=90°,又∵OA=OD,
∴∠A=∠ADO,∴∠AEF=∠CDE.
又∵∠AEF=∠DEC,
∴∠DEC=∠CDE,∴CE=CD.(3)CE=CD仍然成立.连接OD,
∠ODA+∠ADC=90°,在Rt△EAG中,
∠CEA+∠EAG=90°.又∵OA=OD,
∴∠OAD=∠ODA,∴∠OAD+∠ADC=90°.
又∵∠EAG=∠OAD,∴∠CEA=∠CDA,
∴CE=CD.谢谢
同课章节目录
