新人教版九年级上册24.2.2直线和圆的位置关系(第三课时)
文档属性
| 名称 | 新人教版九年级上册24.2.2直线和圆的位置关系(第三课时) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-26 00:00:00 | ||
图片预览








文档简介
课件53张PPT。 1.掌握切线长定理并能利用其进行相关的证明与计算.
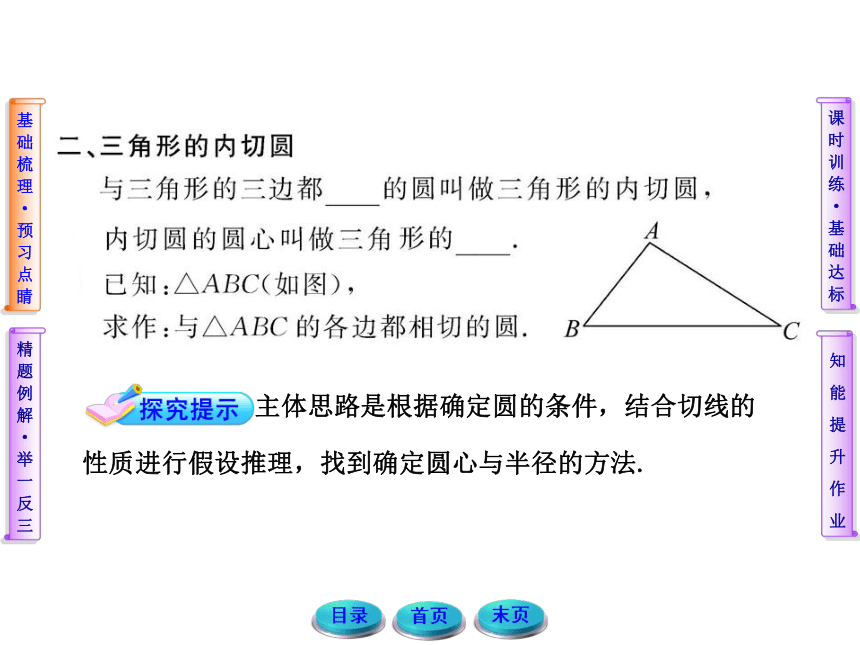
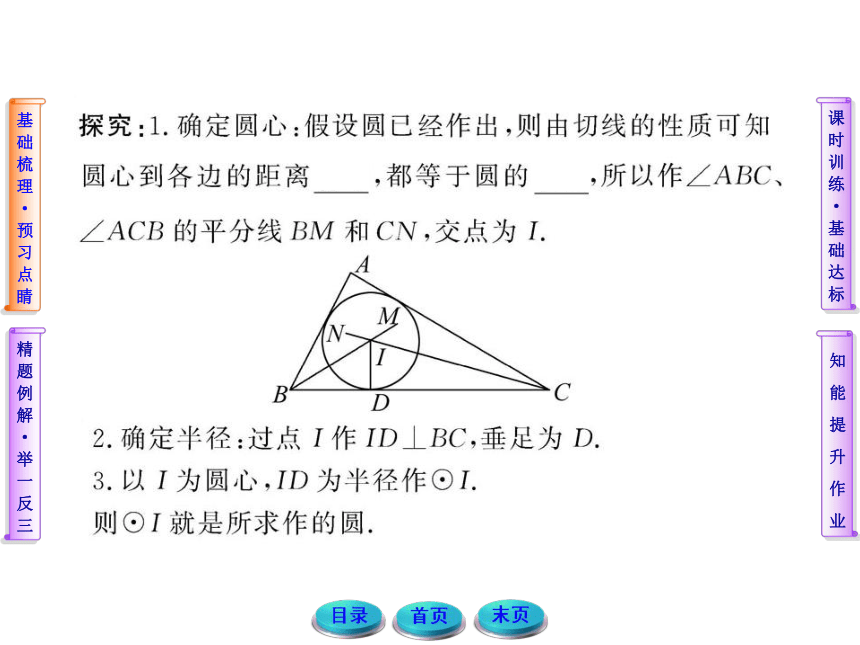
2.掌握三角形内切圆的作法,理解并能应用内心的性质进行相关的证明与计算. 主体思路是根据确定圆的条件,结合切线的性质进行假设推理,找到确定圆心与半径的方法. 切线长定理及其应用
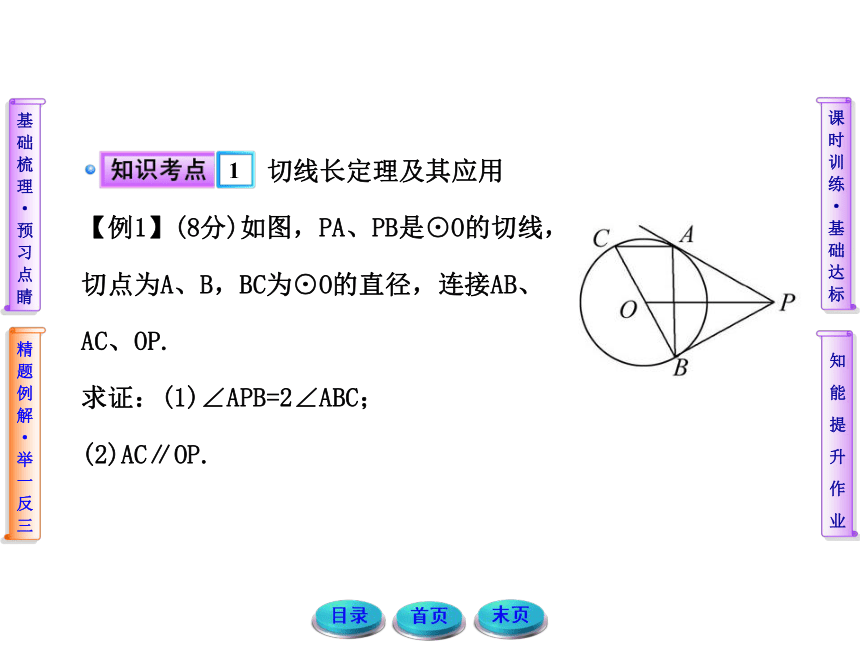
【例1】(8分)如图,PA、PB是⊙O的切线,
切点为A、B,BC为⊙O的直径,连接AB、
AC、OP.
求证:(1)∠APB=2∠ABC;
(2)AC∥OP.【规范解答】(1)∵PA、PB是⊙O的切线,
∴∠APO=∠BPO= ∠APB,PA=PB,……………………1分
∴PO⊥AB,∴∠ABP+∠BPO=90°. ……………………3分
又∵PB是⊙O的切线,∴OB⊥PB,
∴∠ABP+∠ABC=90°.…………………………………4分
∴∠ABC=∠BPO= ∠APB,
即∠APB=2∠ABC.………………………………………5分
(2)∵BC为⊙O的直径,∴∠BAC=90°,
即AC⊥AB.………………………………………………6分
由(1)知PO⊥AB,∴AC∥OP.……………………………8分 切线长定理的图形结构记忆不清,不能正确找到相对应的数量关系,从而找不到正确的解题途径. 切线长定理的基本图形结构涉及到垂直关系、全等关系、等腰三角形、等弧等,是证明线段、角相等及计算的重要依据,应用的前提是理清图形结构中存在的所有关系.1.如图所示,PA、PB是⊙O的切线,且
∠APB=40°,下列说法不正确的是( )
(A)PA=PB (B)∠APO=20° (C)∠OBP=70° (D)∠AOP=70°
【解析】选C.根据切线长定理可知,A、B正确.所以∠AOP=70°,故D也正确,∵PB是⊙O的切线,∴∠OBP=90°,故C错误.2.如图所示,PA、PB是⊙O的切线,CD切
⊙O于E,若PA=4,则△PCD的周长为_____.
【解析】因为CD是⊙O的切线,PA、PB也是
⊙O的切线,所以CE=AC,DE=BD.△PCD周长为PC+PD+CD=PC+PD+AC+BD=(PC+AC)+(PD+BD)=2PA.又因为PA=4,所以△PCD的周长为8.
答案:8 与切线长有关的角度或线段的计算,其关键是理解图形结构中所体现的等量关系及垂直关系,并且经常与切线的性质、勾股定理等结合使用,有时也用到面积法求解. 三角形的内切圆
【例2】已知:如图,⊙O是Rt△ABC的内切圆,D、E、F为切点,∠C是直角,AC=3,BC=4.求⊙O的半径.【思路点拨】【自主解答】连接OE、OF,∴∠OFC=∠OEC=90°.
又∵∠C=90°,∴四边形OECF为矩形.
又∵OF=OE,∴矩形OECF为正方形.
设⊙O的半径为r,则CE=CF=r,
又∵BE=BD,AD=AF,AB=
∴BC-r+AC-r=BD+AD=AB,
即4-r+3-r=5,∴r=1.故⊙O的半径是1. 三角形内切圆的图形结构实质是三个切线长定
理图形结构的组合,在解决此类问题时,常利用切线长定
理,借助方程、方程组模型加以解决.三角形内切圆的半径
与三角形面积的关系:三角形的面积为S△= (a+b+c)·r,
在计算直角三角形内切圆的半径时,可通过勾股定理把S△
求出来,a,b,c三边已知,代入上式可求出内切圆的半径. 3.如图,△ABC中,∠A=45°,I是内心,则∠BIC=( )
(A)112.5° (B)112° (C)125° (D)55°
【解析】选A.因为I是内心,所以
∠IBC= ∠ABC,∠ICB= ∠ACB,
所以∠BIC=180°- (∠ABC+∠ACB)=180°- (180°-45°)
=112.5°.4.如图所示,在△ABC中,AB=AC=10,BC=12,试求△ABC的内切圆的半径长.【解析】设△ABC的内切圆的半径为r.
∵AB=AC,⊙I是△ABC的内切圆.∴AD⊥BC.
∵AB=AC=10,BC=12,
∴
又∵S△ABC= (AB+BC+AC)·r,
即 ×(10+10+12)×r=48,∴r=3.
则△ABC的内切圆的半径长为3. 与三角形内心有关的角度的计算,一般是连接内心和顶点,构造角平分线,结合三角形内角和进行求解. 1.(2010·巴中中考)如图所示,一块三角
形的草坪,现要在草坪上建一凉亭供大家
休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
(A)△ABC的三条中线的交点
(B)△ABC三边的中垂线的交点
(C)△ABC三条角平分线的交点
(D)△ABC三条高所在直线的交点【解析】选C.三角形中,到三边距离相等的点在三条角平分线的交点上.2.若⊙O的切线长和半径相等,则两条切线的夹角的度数为_____.
【解析】如图,由题意知,OA=PA,
所以△POA为等腰直角三角形,所以
∠APO=45°,同理∠BPO=45°.所以
两条切线的夹角的度数为90°.
答案:90°3.(2010·孝感中考)P为⊙O外一点,PA、PB分别切⊙O于点A、B,∠APB=50°,点C为⊙O上一点(不与A、B重合),则∠ACB的度数为_____.【解析】如图,由∠P=50°得∠AOB=180°-50°=130°.分两种情况讨论:若C在优弧上时,如图中的点C1,则∠AC1B=65°;若C在劣弧上时,如图中的点C2,由圆内接四边形的性质可知∠AC2B=180°-65°=115°.
答案:65°或115°4.为了测量一个圆形铁环的半径,某同
学利用本节所学的知识,设计了如下的
测量方案:将铁环平放在水平桌面上,
用一个含有30°角的三角尺(∠B=30°)
和一把刻度尺,按如图所示的方法放置,测得PA=6 cm,请你根据方案及测量的结果求出铁环的半径.(结果保留两个有效数字)【解析】连接AO、PO,∵AP是⊙O的切线,
∴∠OPA=90°.又∵AP、AB是⊙O的两条切线,
∠PAB=120°,由切线长定理得:∠OAP=60°.
在Rt△OAP中,∠POA=90°-60°=30°,PA=6 cm,∴OA=2PA=12 cm.
∴OP= ≈10(cm).一、选择题(每小题4分,共12分)
1.如图,AB、BC、CD分别切⊙O于E、F、G,且AB∥CD,
BO=3 cm,CO=4 cm,则BC等于( )
(A)5 cm (B)6 cm
(C)7 cm (D)8 cm【解析】选A.∵AB、BC为⊙O的切线,
∴OB平分∠ABC,同理OC平分∠BCD,
又∵AB∥CD,∴∠ABC+∠BCD=180°,
∴∠OBC+∠OCB= =90°,
∴∠BOC=180°-90°=90°,
又∵BO=3 cm,CO=4 cm,
∴ =5(cm).2.如图所示,EB、EC是⊙O的两条
切线,B、C是切点,A、D是⊙O上
两点,如果∠E=46°,∠DCF=32°,
则∠A的度数为( )
(A)78° (B)99° (C)81° (D)67°【解析】选B.∵EB、EC是⊙O的两条切线,∴EB=EC,
∴∠ECB=∠EBC,又∠E=46°,
∠E+∠EBC+∠ECB=180°,∴∠ECB=67°,
又∠DCF+∠ECB+∠DCB=180°,
∴∠BCD=180°-67°-32°=81°,
又∠A+∠BCD=180°,∴∠A=180°-81°=99°.3.如图,△ABC中,AB=AC,∠BAC为锐角,CD
为AB边上的高,I为△ACD的内心,则∠AIB的
度数为( )
(A)120° (B)125°
(C)135° (D)150°【解析】选C.连接IC,因为I是△ACD的内心,所以IA、IC分别平分∠BAC、∠ACD,由CD⊥AD,可得∠AIC=135°,又因为AB=AC,所以△ABC为轴对称图形,且对称轴经过顶角的平分线,所以∠AIB=∠AIC=135°. 【归纳整合】与三角形内切圆(内心)有关的角度的计算,主要是利用内心是三条内角平分线的交点,结合三角形的内角和定理、圆周角定理、圆内接四边形性质、切线的性质等知识进行运算,如图,常利用的结论有:
∠EGF=∠BOC=90°+ ∠A,∠EDF=90°- ∠A.二、填空题(每小题4分,共12分)
4.如图,AC⊥BC于点C,BC=a,CA=b,
AB=c,⊙O与直线AB、BC、CA都相切,
则⊙O的半径为_____.
【解析】连接OE、OD,则可知四边形OECD为正方形.由切线
长定理可知,2BD=AB+AC+BC=a+b+c,所以BD= ,
所以OD=CD=BD-BC= .
答案:5.(2010·黔南州中考)如图,PA、
PB是⊙O的切线,AC是⊙O的直径,
∠P=40°,则∠BAC=_____.
【解析】连接OP,则由切线长定理可知∠OPB=∠OPA=20°,∴∠AOP=∠BOP=70°
即∠AOB=140°,∴∠COB=40°,∴∠BAC=20°.
答案:20° 6.如图,在平面直角坐标系中,⊙I与
x轴、y轴分别切于点D、E,I点坐标为
(-1,-1),B点坐标为(0,-4),则
直线AB的解析式为_____.【解析】由题意知,BC=BE=3,OD=OE=1,
设AD长为x,则有(x+3)2=(x+1)2+42,解得x=2.
∴A点坐标为(-3,0),
设AB的解析式为y=kx+b得
答案:三、解答题(共26分)
7.(8分)如图,AB为⊙O的直径,DA、BC分
别切半圆O于点A、B,DC切⊙O于点P,OA=6,
S四边形ABCD=90.
求四边形ABCD各边的长.【解析】过C点作CE⊥AD,垂足为E,∵AD、BC是⊙O的切线,∴AD⊥AB,BC⊥AB,
∴四边形ABCE为矩形,∴CE=AB=2OA=12,设BC=a,AD=b,由切线长定理可知CD=a+b,DE=b-a,∴(a+b)2=(b-a)2+122,整理得ab=36①,根据四边形的面积得:6(a+b)=90,∴a+b=15②,由①、②得a=3,b=12,∴四边形各边的长为:AB=12,BC=3,CD=15,AD=12.8.(8分)(2010·梅州中考)(1)如图1,PA、PB分别与⊙O相切于点A、B.求证:PA=PB.
(2)如图2,过⊙O外一点P的两条直线分别与⊙O相交于点A、B和C、D.那么当_____时,PB=PD(不添加字母符号和辅助线,不需证明,只需填上符合题意的一个条件).【解析】(1)连接OA、OB.
∵PA、PB分别与⊙O相切于点A、B,
∴OA⊥PA,OB⊥PB.
∴∠OAP=∠OBP=90°
又∵OA=OB,OP=OP,
∴△OAP≌△OBP.∴PA=PB.
(2)∠BPO=∠DPO
(答案不惟一,如PA=PC,AB=CD)【拓展延伸】
9.(10分)如图,已知直线y= x+
4k(k>0)与x轴、y轴分别交于点A、B,
⊙O1与x轴、y轴切于点D、E,与AB切于
点C.
(1)若k=1,求⊙O1的半径;
(2)求∠AO1B的度数;
(3)连接OC、CD,当k的值发生变化时,猜想∠OCD的大小是否会发生变化,若不变,求∠OCD的大小;若发生变化,求其变化的范围.【解析】(1)连接O1D、O1E、O1C,
∵⊙O1分别与x轴、y轴、直线AB相切,
∴四边形ODO1E为正方形.
∵⊙O1的半径r=OD=OE,
又∵BC=BE,AD=AC,
∴OA+OB+AB=OD+OE=2r.
当k=1时,A、B两点的坐标分别为A(3,0),B(0,4),∴由勾股定理得AB=5,2r=OA+OB+AB=3+4+5=12,
∴r=6,∴⊙O1的半径为6.(2)由切线长定理可证△AO1C≌△AO1D,△BO1C≌△BO1E,
∴∠BO1C= ∠EO1C,∠AO1C= ∠DO1C,
∠AO1B=∠BO1C+∠AO1C
= (∠EO1C+∠DO1C)=45°.(3)∠OCD的大小不发生变化,理由如下:
∵A(3k,0),B(0,4k),OA=3k,OB=4k,由勾股定理得AB=5k(k>0),由(1)知OD+OE=OA+OB+AB=12k,∴2OD=12k,OD=6k,
又OA=3k,∴AC=AD=6k-3k=3k,
∴OA=AC=AD=3k,
∴点C在以A为圆心,OD为直径的圆上.
∴∠OCD=90°.
∴∠OCD的大小不会改变,其大小为90°.
2.掌握三角形内切圆的作法,理解并能应用内心的性质进行相关的证明与计算. 主体思路是根据确定圆的条件,结合切线的性质进行假设推理,找到确定圆心与半径的方法. 切线长定理及其应用
【例1】(8分)如图,PA、PB是⊙O的切线,
切点为A、B,BC为⊙O的直径,连接AB、
AC、OP.
求证:(1)∠APB=2∠ABC;
(2)AC∥OP.【规范解答】(1)∵PA、PB是⊙O的切线,
∴∠APO=∠BPO= ∠APB,PA=PB,……………………1分
∴PO⊥AB,∴∠ABP+∠BPO=90°. ……………………3分
又∵PB是⊙O的切线,∴OB⊥PB,
∴∠ABP+∠ABC=90°.…………………………………4分
∴∠ABC=∠BPO= ∠APB,
即∠APB=2∠ABC.………………………………………5分
(2)∵BC为⊙O的直径,∴∠BAC=90°,
即AC⊥AB.………………………………………………6分
由(1)知PO⊥AB,∴AC∥OP.……………………………8分 切线长定理的图形结构记忆不清,不能正确找到相对应的数量关系,从而找不到正确的解题途径. 切线长定理的基本图形结构涉及到垂直关系、全等关系、等腰三角形、等弧等,是证明线段、角相等及计算的重要依据,应用的前提是理清图形结构中存在的所有关系.1.如图所示,PA、PB是⊙O的切线,且
∠APB=40°,下列说法不正确的是( )
(A)PA=PB (B)∠APO=20° (C)∠OBP=70° (D)∠AOP=70°
【解析】选C.根据切线长定理可知,A、B正确.所以∠AOP=70°,故D也正确,∵PB是⊙O的切线,∴∠OBP=90°,故C错误.2.如图所示,PA、PB是⊙O的切线,CD切
⊙O于E,若PA=4,则△PCD的周长为_____.
【解析】因为CD是⊙O的切线,PA、PB也是
⊙O的切线,所以CE=AC,DE=BD.△PCD周长为PC+PD+CD=PC+PD+AC+BD=(PC+AC)+(PD+BD)=2PA.又因为PA=4,所以△PCD的周长为8.
答案:8 与切线长有关的角度或线段的计算,其关键是理解图形结构中所体现的等量关系及垂直关系,并且经常与切线的性质、勾股定理等结合使用,有时也用到面积法求解. 三角形的内切圆
【例2】已知:如图,⊙O是Rt△ABC的内切圆,D、E、F为切点,∠C是直角,AC=3,BC=4.求⊙O的半径.【思路点拨】【自主解答】连接OE、OF,∴∠OFC=∠OEC=90°.
又∵∠C=90°,∴四边形OECF为矩形.
又∵OF=OE,∴矩形OECF为正方形.
设⊙O的半径为r,则CE=CF=r,
又∵BE=BD,AD=AF,AB=
∴BC-r+AC-r=BD+AD=AB,
即4-r+3-r=5,∴r=1.故⊙O的半径是1. 三角形内切圆的图形结构实质是三个切线长定
理图形结构的组合,在解决此类问题时,常利用切线长定
理,借助方程、方程组模型加以解决.三角形内切圆的半径
与三角形面积的关系:三角形的面积为S△= (a+b+c)·r,
在计算直角三角形内切圆的半径时,可通过勾股定理把S△
求出来,a,b,c三边已知,代入上式可求出内切圆的半径. 3.如图,△ABC中,∠A=45°,I是内心,则∠BIC=( )
(A)112.5° (B)112° (C)125° (D)55°
【解析】选A.因为I是内心,所以
∠IBC= ∠ABC,∠ICB= ∠ACB,
所以∠BIC=180°- (∠ABC+∠ACB)=180°- (180°-45°)
=112.5°.4.如图所示,在△ABC中,AB=AC=10,BC=12,试求△ABC的内切圆的半径长.【解析】设△ABC的内切圆的半径为r.
∵AB=AC,⊙I是△ABC的内切圆.∴AD⊥BC.
∵AB=AC=10,BC=12,
∴
又∵S△ABC= (AB+BC+AC)·r,
即 ×(10+10+12)×r=48,∴r=3.
则△ABC的内切圆的半径长为3. 与三角形内心有关的角度的计算,一般是连接内心和顶点,构造角平分线,结合三角形内角和进行求解. 1.(2010·巴中中考)如图所示,一块三角
形的草坪,现要在草坪上建一凉亭供大家
休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
(A)△ABC的三条中线的交点
(B)△ABC三边的中垂线的交点
(C)△ABC三条角平分线的交点
(D)△ABC三条高所在直线的交点【解析】选C.三角形中,到三边距离相等的点在三条角平分线的交点上.2.若⊙O的切线长和半径相等,则两条切线的夹角的度数为_____.
【解析】如图,由题意知,OA=PA,
所以△POA为等腰直角三角形,所以
∠APO=45°,同理∠BPO=45°.所以
两条切线的夹角的度数为90°.
答案:90°3.(2010·孝感中考)P为⊙O外一点,PA、PB分别切⊙O于点A、B,∠APB=50°,点C为⊙O上一点(不与A、B重合),则∠ACB的度数为_____.【解析】如图,由∠P=50°得∠AOB=180°-50°=130°.分两种情况讨论:若C在优弧上时,如图中的点C1,则∠AC1B=65°;若C在劣弧上时,如图中的点C2,由圆内接四边形的性质可知∠AC2B=180°-65°=115°.
答案:65°或115°4.为了测量一个圆形铁环的半径,某同
学利用本节所学的知识,设计了如下的
测量方案:将铁环平放在水平桌面上,
用一个含有30°角的三角尺(∠B=30°)
和一把刻度尺,按如图所示的方法放置,测得PA=6 cm,请你根据方案及测量的结果求出铁环的半径.(结果保留两个有效数字)【解析】连接AO、PO,∵AP是⊙O的切线,
∴∠OPA=90°.又∵AP、AB是⊙O的两条切线,
∠PAB=120°,由切线长定理得:∠OAP=60°.
在Rt△OAP中,∠POA=90°-60°=30°,PA=6 cm,∴OA=2PA=12 cm.
∴OP= ≈10(cm).一、选择题(每小题4分,共12分)
1.如图,AB、BC、CD分别切⊙O于E、F、G,且AB∥CD,
BO=3 cm,CO=4 cm,则BC等于( )
(A)5 cm (B)6 cm
(C)7 cm (D)8 cm【解析】选A.∵AB、BC为⊙O的切线,
∴OB平分∠ABC,同理OC平分∠BCD,
又∵AB∥CD,∴∠ABC+∠BCD=180°,
∴∠OBC+∠OCB= =90°,
∴∠BOC=180°-90°=90°,
又∵BO=3 cm,CO=4 cm,
∴ =5(cm).2.如图所示,EB、EC是⊙O的两条
切线,B、C是切点,A、D是⊙O上
两点,如果∠E=46°,∠DCF=32°,
则∠A的度数为( )
(A)78° (B)99° (C)81° (D)67°【解析】选B.∵EB、EC是⊙O的两条切线,∴EB=EC,
∴∠ECB=∠EBC,又∠E=46°,
∠E+∠EBC+∠ECB=180°,∴∠ECB=67°,
又∠DCF+∠ECB+∠DCB=180°,
∴∠BCD=180°-67°-32°=81°,
又∠A+∠BCD=180°,∴∠A=180°-81°=99°.3.如图,△ABC中,AB=AC,∠BAC为锐角,CD
为AB边上的高,I为△ACD的内心,则∠AIB的
度数为( )
(A)120° (B)125°
(C)135° (D)150°【解析】选C.连接IC,因为I是△ACD的内心,所以IA、IC分别平分∠BAC、∠ACD,由CD⊥AD,可得∠AIC=135°,又因为AB=AC,所以△ABC为轴对称图形,且对称轴经过顶角的平分线,所以∠AIB=∠AIC=135°. 【归纳整合】与三角形内切圆(内心)有关的角度的计算,主要是利用内心是三条内角平分线的交点,结合三角形的内角和定理、圆周角定理、圆内接四边形性质、切线的性质等知识进行运算,如图,常利用的结论有:
∠EGF=∠BOC=90°+ ∠A,∠EDF=90°- ∠A.二、填空题(每小题4分,共12分)
4.如图,AC⊥BC于点C,BC=a,CA=b,
AB=c,⊙O与直线AB、BC、CA都相切,
则⊙O的半径为_____.
【解析】连接OE、OD,则可知四边形OECD为正方形.由切线
长定理可知,2BD=AB+AC+BC=a+b+c,所以BD= ,
所以OD=CD=BD-BC= .
答案:5.(2010·黔南州中考)如图,PA、
PB是⊙O的切线,AC是⊙O的直径,
∠P=40°,则∠BAC=_____.
【解析】连接OP,则由切线长定理可知∠OPB=∠OPA=20°,∴∠AOP=∠BOP=70°
即∠AOB=140°,∴∠COB=40°,∴∠BAC=20°.
答案:20° 6.如图,在平面直角坐标系中,⊙I与
x轴、y轴分别切于点D、E,I点坐标为
(-1,-1),B点坐标为(0,-4),则
直线AB的解析式为_____.【解析】由题意知,BC=BE=3,OD=OE=1,
设AD长为x,则有(x+3)2=(x+1)2+42,解得x=2.
∴A点坐标为(-3,0),
设AB的解析式为y=kx+b得
答案:三、解答题(共26分)
7.(8分)如图,AB为⊙O的直径,DA、BC分
别切半圆O于点A、B,DC切⊙O于点P,OA=6,
S四边形ABCD=90.
求四边形ABCD各边的长.【解析】过C点作CE⊥AD,垂足为E,∵AD、BC是⊙O的切线,∴AD⊥AB,BC⊥AB,
∴四边形ABCE为矩形,∴CE=AB=2OA=12,设BC=a,AD=b,由切线长定理可知CD=a+b,DE=b-a,∴(a+b)2=(b-a)2+122,整理得ab=36①,根据四边形的面积得:6(a+b)=90,∴a+b=15②,由①、②得a=3,b=12,∴四边形各边的长为:AB=12,BC=3,CD=15,AD=12.8.(8分)(2010·梅州中考)(1)如图1,PA、PB分别与⊙O相切于点A、B.求证:PA=PB.
(2)如图2,过⊙O外一点P的两条直线分别与⊙O相交于点A、B和C、D.那么当_____时,PB=PD(不添加字母符号和辅助线,不需证明,只需填上符合题意的一个条件).【解析】(1)连接OA、OB.
∵PA、PB分别与⊙O相切于点A、B,
∴OA⊥PA,OB⊥PB.
∴∠OAP=∠OBP=90°
又∵OA=OB,OP=OP,
∴△OAP≌△OBP.∴PA=PB.
(2)∠BPO=∠DPO
(答案不惟一,如PA=PC,AB=CD)【拓展延伸】
9.(10分)如图,已知直线y= x+
4k(k>0)与x轴、y轴分别交于点A、B,
⊙O1与x轴、y轴切于点D、E,与AB切于
点C.
(1)若k=1,求⊙O1的半径;
(2)求∠AO1B的度数;
(3)连接OC、CD,当k的值发生变化时,猜想∠OCD的大小是否会发生变化,若不变,求∠OCD的大小;若发生变化,求其变化的范围.【解析】(1)连接O1D、O1E、O1C,
∵⊙O1分别与x轴、y轴、直线AB相切,
∴四边形ODO1E为正方形.
∵⊙O1的半径r=OD=OE,
又∵BC=BE,AD=AC,
∴OA+OB+AB=OD+OE=2r.
当k=1时,A、B两点的坐标分别为A(3,0),B(0,4),∴由勾股定理得AB=5,2r=OA+OB+AB=3+4+5=12,
∴r=6,∴⊙O1的半径为6.(2)由切线长定理可证△AO1C≌△AO1D,△BO1C≌△BO1E,
∴∠BO1C= ∠EO1C,∠AO1C= ∠DO1C,
∠AO1B=∠BO1C+∠AO1C
= (∠EO1C+∠DO1C)=45°.(3)∠OCD的大小不发生变化,理由如下:
∵A(3k,0),B(0,4k),OA=3k,OB=4k,由勾股定理得AB=5k(k>0),由(1)知OD+OE=OA+OB+AB=12k,∴2OD=12k,OD=6k,
又OA=3k,∴AC=AD=6k-3k=3k,
∴OA=AC=AD=3k,
∴点C在以A为圆心,OD为直径的圆上.
∴∠OCD=90°.
∴∠OCD的大小不会改变,其大小为90°.
同课章节目录
