新人教版九年级上册24.1.4圆周角
文档属性
| 名称 | 新人教版九年级上册24.1.4圆周角 |
|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-26 00:00:00 | ||
图片预览










文档简介
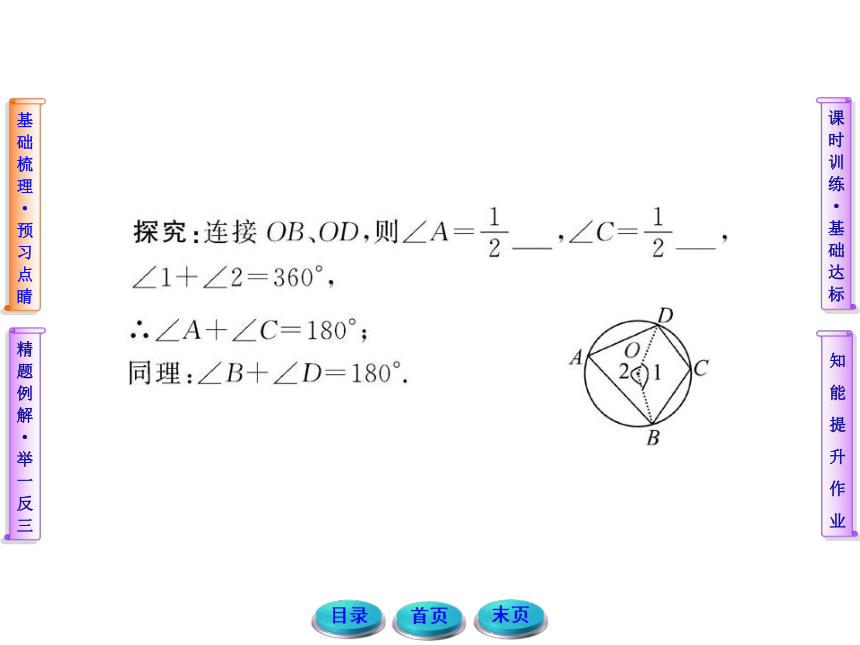
课件52张PPT。 掌握圆周角定义,会判断某角是否是圆周角;掌握圆周角定理及其推论,并利用其解决问题. 掌握圆内接四边形的性质及其应用. 连接半径,构造同弧所对的圆心角,利用同弧所对的圆周角等于圆心角度数的一半解决问题. 圆周角定理及其推论的应用
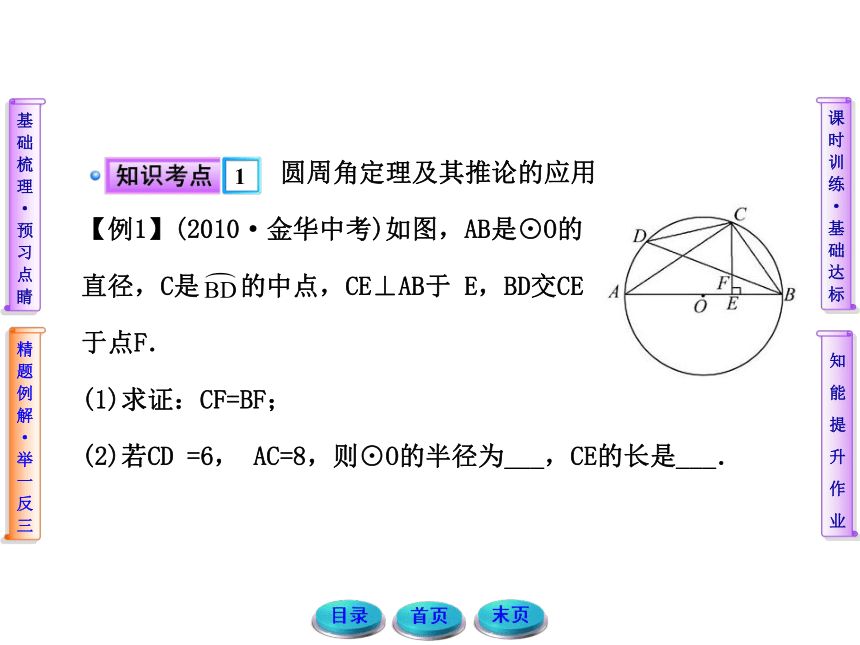
【例1】(2010·金华中考)如图,AB是⊙O的
直径,C是 的中点,CE⊥AB于 E,BD交CE
于点F.
(1)求证:CF=BF;
(2)若CD =6, AC=8,则⊙O的半径为___,CE的长是___.【思路点拨】由直径所对的圆周角是直角,同角的余角相等,等弧所对的圆周角相等证明角的相等进而得到线段的相等.求半径及面积时应用勾股定理及等积法.【自主解答】(1) ∵AB是⊙O的直径,∴∠ACB=90°
又∵CE⊥AB,∴∠CEB=90°,∴∠BCE=90°-∠CBE=∠A
又∵C是弧BD的中点,∴∠CBF=∠A,∴∠BCE=∠CBF,
∴ CF=BF.
(2)由(1)知:BC=CD=6,∴AB= =10,∴⊙O的半径
为5,
∵AC·BC=AB·CE,∴CE= ,∴CE的长是 . 1.在圆中的证明或计算需要使用角的相等时,一般的方法是构造同弧或等弧所对的圆周角相等,应用的关键是灵活地对角进行转换.
2.在圆中,若有直径时,构造“直径所对的圆周角是直角”是常用的添加辅助线的方法;条件中有90°的圆周角时,一般用该圆周角所对的弦表示直径.
3.在解题时注意勾股定理、垂径定理的应用.1.(2010·南昌中考)如图,⊙O 中,AB、AC是弦,O在∠BAC的内部,∠ABO=α,∠ACO=β,∠BOC=θ,则下列关系中,正确的是 ( )
(A)θ=α+β (B)θ=2α+2β
(C)α+β+θ=180° (D)α+β+θ=360°
【解析】选B.连接AO,则∠BAO=∠ABO=α,∠CAO=∠ACO=β,所以∠BOC=2∠BAC,即θ=2α+2β.2.(2010·淮安中考)如图,已知点A,B,
C在⊙O上,AC∥OB,∠BOC=40°,
则∠ABO=_____.
【解析】由同弧上的圆周角等于该弧上圆心角的一半,
所以∠BAC= ∠BOC= ×40°=20°,又AC∥OB,
所以∠ABO=20°.
答案:20°3.(2010·赤峰中考)如图,AB是⊙O的一条弦,
OD⊥AB,垂足为C,交⊙O于一点D,点E在⊙O上,
∠AED=25°,则∠OBA的度数是_____.
【解析】∵OD⊥AB,∴ ,∴∠BOD=2∠AED=50°,
∴∠OBA =90°-50°=40°.
答案:40° 解题的关键是把握同弧或等弧所对的圆周角、圆心角之间的倍数关系;有直径时,利用直径所对的圆周角是直角并构造直径所对的圆周角;垂径定理构造了等弧,为角的相等提供了更多的转换途径,解题时要灵活转化. 圆内接四边形
【例2】如图所示,已知圆心角∠AOB=100°,求∠ACD的度数.【思路点拨】【自主解答】如图,在优弧 上任取点E,连接AE,BE,
则∠E= ∠AOB=50°,
∴∠ACB=130°,
∴∠ACD=180°-∠ACB=50°. 圆内接四边形对角互补,结合邻补角还可以得到“圆内接四边形的外角等于与它不相邻的内对角”.计算弧所“含”的圆周角的度数,往往构造弧所对的圆周角,利用圆内接四边形的性质结合同弧所对的圆周角、圆心角之间的关系来解决.4.圆内接四边形相邻三个内角度数的比为2∶1∶7,则其最大内角的度数为_____.
【解析】根据圆内接四边形的对角互补可知,其对角和相
等,所以四个内角的度数的比为2∶1∶7∶8,又因为四边形
的内角和为360°,所以最大内角的度数为
360°× =160°.
答案:160°5.(2010·威海中考)如图,AB为⊙O的
直径,点C,D在⊙O上.若∠AOD=30°,
则∠BCD的度数是_____.
【解析】连接BD,∵AB为⊙O的直径,∴∠ADB=90°,
∵∠AOD=30°,∴∠ABD=15°,
∴∠DAB=90°-15°=75°,∴∠BCD=180°-75°=105°.
答案:105° 涉及到圆内接四边形的度数比的问题,一般是根据圆内接四边形的性质,求出所有内角的比值,应用比例性质或结合方程的思想来解决.解题时注意圆周角定理及其推论的灵活应用. 1.(2010·清远中考)下列各图中,∠1=∠2的是( )
【解析】选D.同弧所对的圆周角相等.2.圆内接平行四边形一定是( )
(A)矩形 (B) 正方形 (C) 菱形 (D)梯形
【解析】选A.由圆内接四边形的对角互补及平行四边形对角相等得,四边形的四个角都是直角,故选A.3.如图,AB是⊙O的直径,C、D、E都是⊙O上
的点,则∠C+∠D=_____.
【解析】连接AE、BE,则∠C=∠EBA,
∠D=∠EAB,又∵AB是⊙O的直径,
∴∠AEB=90°,∴∠C+∠D=90°.
答案:90°4.(2010·娄底中考)如图,在半径为R的⊙O
中,弦AB的长与半径R相等,C是优弧 上一
点,则∠ACB的度数是_____.
【解析】连接OA、OB,∵弦AB的长与半径R相等,∴△OAB为等边三角形,
∴∠AOB=60°,∴∠ACB=30°.
答案:30°一、选择题(每小题4分,共12分)
1.(2010 ·贵阳中考)如图,AB是⊙O的
直径,C是⊙O上的一点,若AC=8,AB=10,
OD⊥BC于点D,则BD的长为( )
(A)1.5 (B)3 (C)5 (D)6 【解析】选B.∵AB是⊙O的直径,∴∠C=90°,在Rt△ABC
中,BC= ,
又∵OD⊥BC∴BD= BC=3.2.如图,已知EF是⊙O的直径,把∠A为
60°的直角三角板ABC的一条直角边BC
放在直线EF上,斜边AB与⊙O交于点P,
点B与点O重合;将三角板ABC沿OE方向平移,直到点B与点E重合为止,设∠POF=x°,则x的取值范围是( )
(A)30≤x≤60 (B)30≤x≤90
(C)30≤x≤120 (D)60≤x≤120【解析】选A.由题意知,三角板从O向E移动时,∠POF逐渐增大,当点B在圆心的位置时,∠POF=30°,当点B与E重合时,由圆心角、圆周角之间的关系可得∠POF=60°,故选A.3.已知点A、B、C在半径为2 cm的⊙O上,若BC=2 cm,则
∠A的度数为( )
(A)60° (B)120° (C)60°或120° (D)30°【解析】选C.当点A在弦BC所对的优弧上时,如图1,连接BO并延长交⊙O于D,连接CD,OC,则BD=4 cm.
∵BD是⊙O的直径,∴∠BCD=90°.
在Rt△BCD中,
又∵OD=OC=2cm,∴△OCD为等边三角形.
∴∠D=60°.
根据同弧所对的圆周角相等可得∠A=60°.当点A在弦BC所对的劣弧上时,如图2,
由前面的方法,可得∠D=60°,
∴∠A=120°.
∴∠A的度数是60°或120°.二、填空题(每小题4分,共12分)
4.(2010 ·成都中考)如图,在△ABC中,
AB为⊙O的直径,∠B=60°,∠C=70°,则
∠BOD的度数是____度.
【解析】∠A=180°-60°-70°=50°,
所以∠BOD=2∠A=100°.
答案:1005.(2010·南宁中考)如图,AB为半圆O的直径,OC⊥AB,OD平分∠BOC,交半圆于点D,AD交OC于点E,则∠AEO的度数是_____°.
【解析】∵OC⊥AB,OD平分∠BOC,
∴∠BOD=45°,∴∠EAO=22.5°,
∴∠AEO=67.5°.
答案:67.56.如图,点C、D在以AB为直径的⊙O上,且CD平分∠ACB,若AB=2,∠CBA=15°,则CD的长为_____.【解析】如图,连接BD、AD、OD,过O点作OE⊥CD,
∵AB为⊙O的直径,且CD平分∠ACB,
∴△ABD为等腰直角三角形,
∴OD= AB=1,
∠ODA=45°,∠CDA=∠CBA=15°,
∴∠ODE=45°-15°=30°,
∴OE= ,DE= ,∴CD=2DE= .
答案: 【归纳整合】构造直径所对的圆周角是解决与圆相关的问题时常用的辅助线,为勾股定理、垂径定理等知识的应用创造了条件;利用圆周角的性质解题,一般有两种转化方式:一是利用同弧所对的圆周角相等,进行角与角之间的转化;二是角的相等转化为线段(弦)的相等.三、解答题(共26分)
7.(8分)如图所示,⊙O的直径AC=2,∠BAD=75°,∠ACD=45°,则四边形ABCD的周长和面积各为多少?(结果取准确值)【解析】∵四边形ABCD为圆内接四边形,
∴∠BCD=180°-∠BAD=180°-75°=105°,
∴∠BCA=105°-45°=60°.
又∵AC为⊙O的直径,∴∠B=∠D=90°,
∴∠BAC=30°,∠CAD=45°.
在Rt△ABC中,BC= AC=1,AB=
在Rt△ACD中,CD=AD= AC= ,
∴四边形ABCD的周长为:
面积为:8.(8分)如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的边于G,F,E点.
求证:(1)F是BC的中点;(2)∠A=∠GEF.【证明】(1)连接DF,
∵∠ACB=90°,D是AB的中点,
∴BD=DC= AB,
∵DC是⊙O的直径,∴DF⊥BC,
∴BF=FC,即F是BC的中点.
(2)∵D,F分别是AB,BC的中点,
∴DF∥AC,∴∠A=∠BDF,
∵∠BDF=∠GEF,∴∠A=∠GEF.【拓展延伸】
9.(10分)如图1所示,已知AB是⊙O的一条弦,点C为 的中
点,CD是⊙O的直径,过C点的直线l交AB所在直线于点E,交⊙O
于点F,
(1)判定图中∠CEB与∠FDC的数量关系,并写出结论.
(2)将直线l绕C点旋转(l与CD不重合),在旋转过程中,E点、
F点的位置也随之变化,请你在下面两个备用图中分别画出l
在不同位置时,使(1)的结论仍然成立的图形,标上相应的字
母,选其中一个图形给予证明.【解析】(1)∠CEB=∠FDC.理由:∵C为 的中点,∴CD⊥AB,
∴∠CEB+∠ECD=90°,又∵CD是⊙O的直径,
∴∠FDC+∠ECD=90°,∴∠CEB=∠FDC.
(2)可以画出直线l经过A点及其他情形时的图形,见图2、图3、图4.对于图2、图3、图4的证明可仿(1)进行,对于图4的证明如下:
∵点C是 的中点,
∴CD⊥AB,∴∠CEB+∠ECD=90°,
又∵CD是⊙O的直径,∴∠CFD=90°,
∴∠FDC+∠ECD=90°,∴∠CEB=∠FDC.
【例1】(2010·金华中考)如图,AB是⊙O的
直径,C是 的中点,CE⊥AB于 E,BD交CE
于点F.
(1)求证:CF=BF;
(2)若CD =6, AC=8,则⊙O的半径为___,CE的长是___.【思路点拨】由直径所对的圆周角是直角,同角的余角相等,等弧所对的圆周角相等证明角的相等进而得到线段的相等.求半径及面积时应用勾股定理及等积法.【自主解答】(1) ∵AB是⊙O的直径,∴∠ACB=90°
又∵CE⊥AB,∴∠CEB=90°,∴∠BCE=90°-∠CBE=∠A
又∵C是弧BD的中点,∴∠CBF=∠A,∴∠BCE=∠CBF,
∴ CF=BF.
(2)由(1)知:BC=CD=6,∴AB= =10,∴⊙O的半径
为5,
∵AC·BC=AB·CE,∴CE= ,∴CE的长是 . 1.在圆中的证明或计算需要使用角的相等时,一般的方法是构造同弧或等弧所对的圆周角相等,应用的关键是灵活地对角进行转换.
2.在圆中,若有直径时,构造“直径所对的圆周角是直角”是常用的添加辅助线的方法;条件中有90°的圆周角时,一般用该圆周角所对的弦表示直径.
3.在解题时注意勾股定理、垂径定理的应用.1.(2010·南昌中考)如图,⊙O 中,AB、AC是弦,O在∠BAC的内部,∠ABO=α,∠ACO=β,∠BOC=θ,则下列关系中,正确的是 ( )
(A)θ=α+β (B)θ=2α+2β
(C)α+β+θ=180° (D)α+β+θ=360°
【解析】选B.连接AO,则∠BAO=∠ABO=α,∠CAO=∠ACO=β,所以∠BOC=2∠BAC,即θ=2α+2β.2.(2010·淮安中考)如图,已知点A,B,
C在⊙O上,AC∥OB,∠BOC=40°,
则∠ABO=_____.
【解析】由同弧上的圆周角等于该弧上圆心角的一半,
所以∠BAC= ∠BOC= ×40°=20°,又AC∥OB,
所以∠ABO=20°.
答案:20°3.(2010·赤峰中考)如图,AB是⊙O的一条弦,
OD⊥AB,垂足为C,交⊙O于一点D,点E在⊙O上,
∠AED=25°,则∠OBA的度数是_____.
【解析】∵OD⊥AB,∴ ,∴∠BOD=2∠AED=50°,
∴∠OBA =90°-50°=40°.
答案:40° 解题的关键是把握同弧或等弧所对的圆周角、圆心角之间的倍数关系;有直径时,利用直径所对的圆周角是直角并构造直径所对的圆周角;垂径定理构造了等弧,为角的相等提供了更多的转换途径,解题时要灵活转化. 圆内接四边形
【例2】如图所示,已知圆心角∠AOB=100°,求∠ACD的度数.【思路点拨】【自主解答】如图,在优弧 上任取点E,连接AE,BE,
则∠E= ∠AOB=50°,
∴∠ACB=130°,
∴∠ACD=180°-∠ACB=50°. 圆内接四边形对角互补,结合邻补角还可以得到“圆内接四边形的外角等于与它不相邻的内对角”.计算弧所“含”的圆周角的度数,往往构造弧所对的圆周角,利用圆内接四边形的性质结合同弧所对的圆周角、圆心角之间的关系来解决.4.圆内接四边形相邻三个内角度数的比为2∶1∶7,则其最大内角的度数为_____.
【解析】根据圆内接四边形的对角互补可知,其对角和相
等,所以四个内角的度数的比为2∶1∶7∶8,又因为四边形
的内角和为360°,所以最大内角的度数为
360°× =160°.
答案:160°5.(2010·威海中考)如图,AB为⊙O的
直径,点C,D在⊙O上.若∠AOD=30°,
则∠BCD的度数是_____.
【解析】连接BD,∵AB为⊙O的直径,∴∠ADB=90°,
∵∠AOD=30°,∴∠ABD=15°,
∴∠DAB=90°-15°=75°,∴∠BCD=180°-75°=105°.
答案:105° 涉及到圆内接四边形的度数比的问题,一般是根据圆内接四边形的性质,求出所有内角的比值,应用比例性质或结合方程的思想来解决.解题时注意圆周角定理及其推论的灵活应用. 1.(2010·清远中考)下列各图中,∠1=∠2的是( )
【解析】选D.同弧所对的圆周角相等.2.圆内接平行四边形一定是( )
(A)矩形 (B) 正方形 (C) 菱形 (D)梯形
【解析】选A.由圆内接四边形的对角互补及平行四边形对角相等得,四边形的四个角都是直角,故选A.3.如图,AB是⊙O的直径,C、D、E都是⊙O上
的点,则∠C+∠D=_____.
【解析】连接AE、BE,则∠C=∠EBA,
∠D=∠EAB,又∵AB是⊙O的直径,
∴∠AEB=90°,∴∠C+∠D=90°.
答案:90°4.(2010·娄底中考)如图,在半径为R的⊙O
中,弦AB的长与半径R相等,C是优弧 上一
点,则∠ACB的度数是_____.
【解析】连接OA、OB,∵弦AB的长与半径R相等,∴△OAB为等边三角形,
∴∠AOB=60°,∴∠ACB=30°.
答案:30°一、选择题(每小题4分,共12分)
1.(2010 ·贵阳中考)如图,AB是⊙O的
直径,C是⊙O上的一点,若AC=8,AB=10,
OD⊥BC于点D,则BD的长为( )
(A)1.5 (B)3 (C)5 (D)6 【解析】选B.∵AB是⊙O的直径,∴∠C=90°,在Rt△ABC
中,BC= ,
又∵OD⊥BC∴BD= BC=3.2.如图,已知EF是⊙O的直径,把∠A为
60°的直角三角板ABC的一条直角边BC
放在直线EF上,斜边AB与⊙O交于点P,
点B与点O重合;将三角板ABC沿OE方向平移,直到点B与点E重合为止,设∠POF=x°,则x的取值范围是( )
(A)30≤x≤60 (B)30≤x≤90
(C)30≤x≤120 (D)60≤x≤120【解析】选A.由题意知,三角板从O向E移动时,∠POF逐渐增大,当点B在圆心的位置时,∠POF=30°,当点B与E重合时,由圆心角、圆周角之间的关系可得∠POF=60°,故选A.3.已知点A、B、C在半径为2 cm的⊙O上,若BC=2 cm,则
∠A的度数为( )
(A)60° (B)120° (C)60°或120° (D)30°【解析】选C.当点A在弦BC所对的优弧上时,如图1,连接BO并延长交⊙O于D,连接CD,OC,则BD=4 cm.
∵BD是⊙O的直径,∴∠BCD=90°.
在Rt△BCD中,
又∵OD=OC=2cm,∴△OCD为等边三角形.
∴∠D=60°.
根据同弧所对的圆周角相等可得∠A=60°.当点A在弦BC所对的劣弧上时,如图2,
由前面的方法,可得∠D=60°,
∴∠A=120°.
∴∠A的度数是60°或120°.二、填空题(每小题4分,共12分)
4.(2010 ·成都中考)如图,在△ABC中,
AB为⊙O的直径,∠B=60°,∠C=70°,则
∠BOD的度数是____度.
【解析】∠A=180°-60°-70°=50°,
所以∠BOD=2∠A=100°.
答案:1005.(2010·南宁中考)如图,AB为半圆O的直径,OC⊥AB,OD平分∠BOC,交半圆于点D,AD交OC于点E,则∠AEO的度数是_____°.
【解析】∵OC⊥AB,OD平分∠BOC,
∴∠BOD=45°,∴∠EAO=22.5°,
∴∠AEO=67.5°.
答案:67.56.如图,点C、D在以AB为直径的⊙O上,且CD平分∠ACB,若AB=2,∠CBA=15°,则CD的长为_____.【解析】如图,连接BD、AD、OD,过O点作OE⊥CD,
∵AB为⊙O的直径,且CD平分∠ACB,
∴△ABD为等腰直角三角形,
∴OD= AB=1,
∠ODA=45°,∠CDA=∠CBA=15°,
∴∠ODE=45°-15°=30°,
∴OE= ,DE= ,∴CD=2DE= .
答案: 【归纳整合】构造直径所对的圆周角是解决与圆相关的问题时常用的辅助线,为勾股定理、垂径定理等知识的应用创造了条件;利用圆周角的性质解题,一般有两种转化方式:一是利用同弧所对的圆周角相等,进行角与角之间的转化;二是角的相等转化为线段(弦)的相等.三、解答题(共26分)
7.(8分)如图所示,⊙O的直径AC=2,∠BAD=75°,∠ACD=45°,则四边形ABCD的周长和面积各为多少?(结果取准确值)【解析】∵四边形ABCD为圆内接四边形,
∴∠BCD=180°-∠BAD=180°-75°=105°,
∴∠BCA=105°-45°=60°.
又∵AC为⊙O的直径,∴∠B=∠D=90°,
∴∠BAC=30°,∠CAD=45°.
在Rt△ABC中,BC= AC=1,AB=
在Rt△ACD中,CD=AD= AC= ,
∴四边形ABCD的周长为:
面积为:8.(8分)如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的边于G,F,E点.
求证:(1)F是BC的中点;(2)∠A=∠GEF.【证明】(1)连接DF,
∵∠ACB=90°,D是AB的中点,
∴BD=DC= AB,
∵DC是⊙O的直径,∴DF⊥BC,
∴BF=FC,即F是BC的中点.
(2)∵D,F分别是AB,BC的中点,
∴DF∥AC,∴∠A=∠BDF,
∵∠BDF=∠GEF,∴∠A=∠GEF.【拓展延伸】
9.(10分)如图1所示,已知AB是⊙O的一条弦,点C为 的中
点,CD是⊙O的直径,过C点的直线l交AB所在直线于点E,交⊙O
于点F,
(1)判定图中∠CEB与∠FDC的数量关系,并写出结论.
(2)将直线l绕C点旋转(l与CD不重合),在旋转过程中,E点、
F点的位置也随之变化,请你在下面两个备用图中分别画出l
在不同位置时,使(1)的结论仍然成立的图形,标上相应的字
母,选其中一个图形给予证明.【解析】(1)∠CEB=∠FDC.理由:∵C为 的中点,∴CD⊥AB,
∴∠CEB+∠ECD=90°,又∵CD是⊙O的直径,
∴∠FDC+∠ECD=90°,∴∠CEB=∠FDC.
(2)可以画出直线l经过A点及其他情形时的图形,见图2、图3、图4.对于图2、图3、图4的证明可仿(1)进行,对于图4的证明如下:
∵点C是 的中点,
∴CD⊥AB,∴∠CEB+∠ECD=90°,
又∵CD是⊙O的直径,∴∠CFD=90°,
∴∠FDC+∠ECD=90°,∴∠CEB=∠FDC.
同课章节目录
