垂直于弦的直径

课件20张PPT。24.1.2 垂径定理九年级数学组　把一个圆沿着它的任意一条直径对折，重复几次，你发现了什么？由此你能得到什么结论？可以发现：1.圆是轴对称图形，任何一条直径所在直线都是它的对称轴．　活动一2.圆是中心对称图形,对称中心是圆心。3.圆具有旋转不变性.如图，AB是⊙O的一条弦，做直径CD，使CD⊥AB，垂足为E．
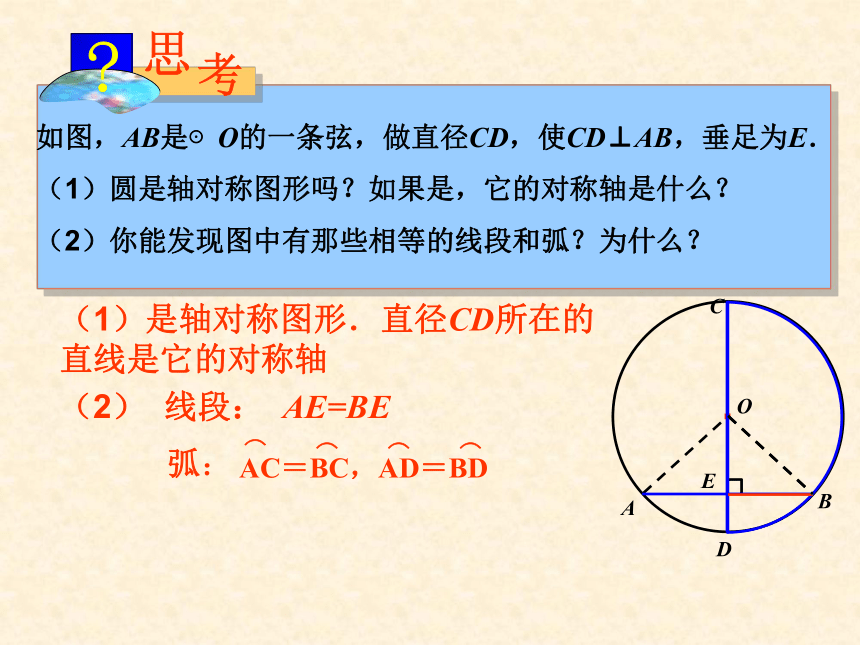
（1）圆是轴对称图形吗？如果是，它的对称轴是什么？
（2）你能发现图中有那些相等的线段和弧？为什么？·OABCDE（1）是轴对称图形．直径CD所在的直线是它的对称轴说理叠 合 法证明：连结OA、OB，则OA＝OB。
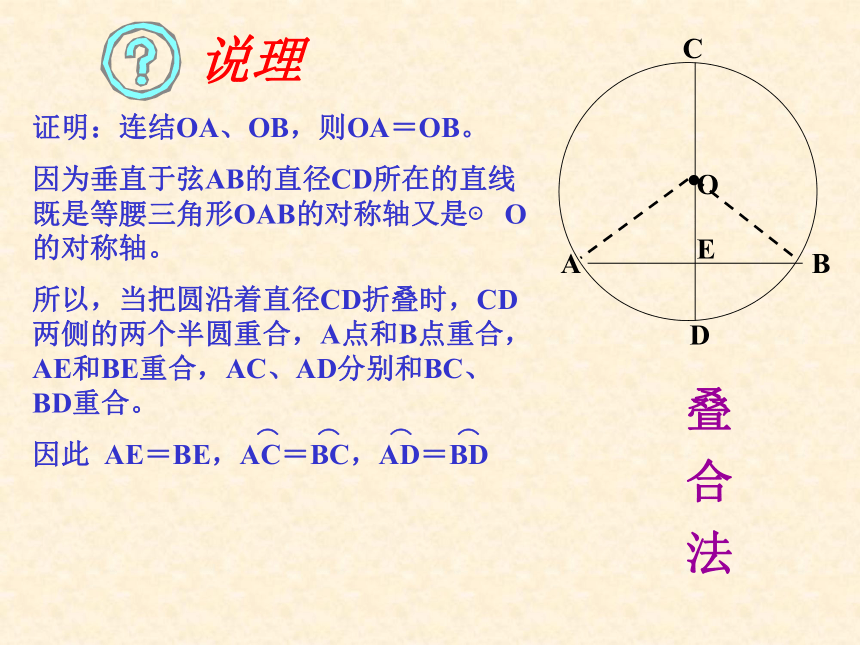
因为垂直于弦AB的直径CD所在的直线既是等腰三角形OAB的对称轴又是⊙ O的对称轴。
所以，当把圆沿着直径CD折叠时，CD两侧的两个半圆重合，A点和B点重合，AE和BE重合，AC、AD分别和BC、 BD重合。
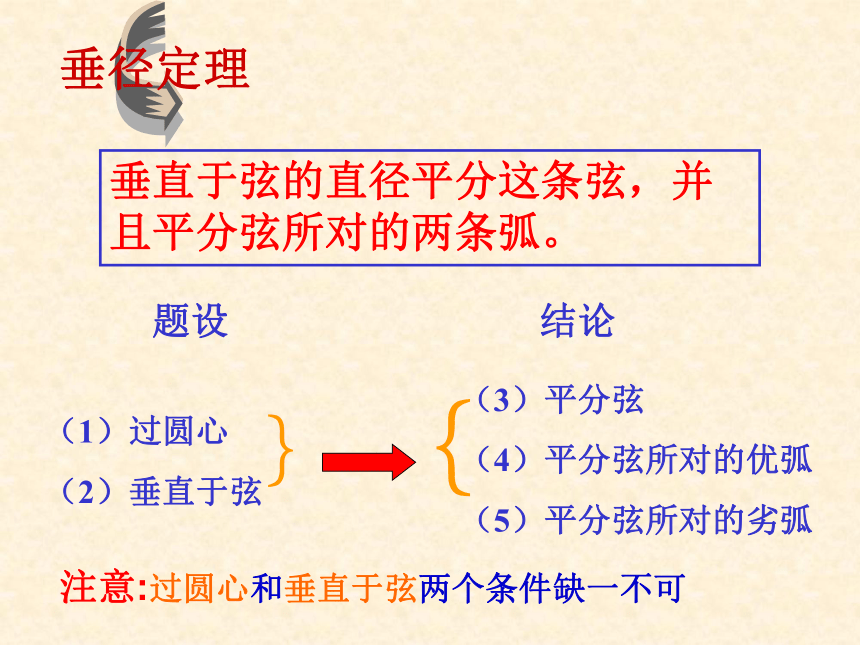
因此 AE＝BE，AC＝BC，AD＝BD⌒⌒⌒⌒垂径定理垂直于弦的直径平分这条弦，并且平分弦所对的两条弧。题设结论（1）过圆心
（2）垂直于弦｝｛（3）平分弦
（4）平分弦所对的优弧
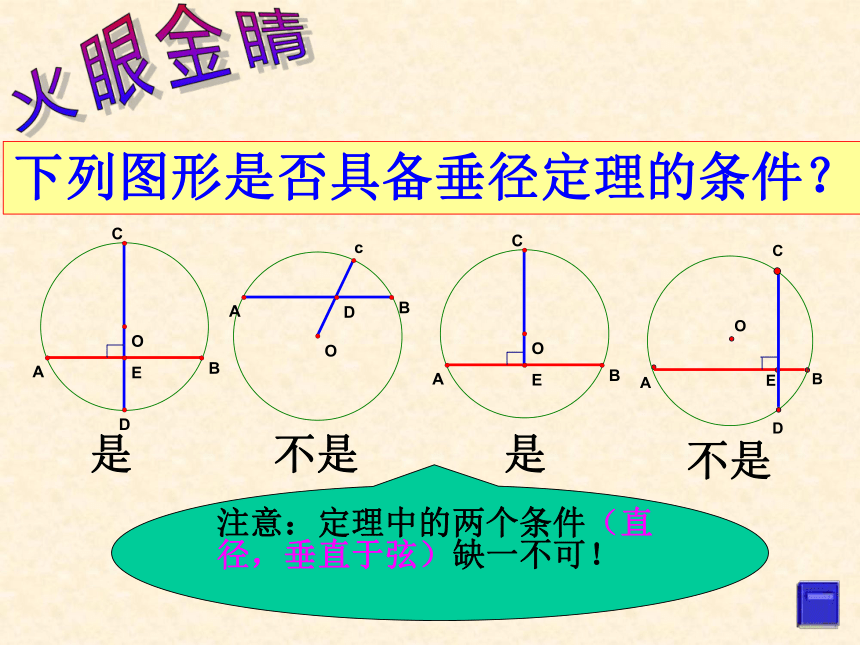
（5）平分弦所对的劣弧注意:过圆心和垂直于弦两个条件缺一不可下列图形是否具备垂径定理的条件？是不是是火眼金睛不是注意：定理中的两个条件（直径，垂直于弦）缺一不可！
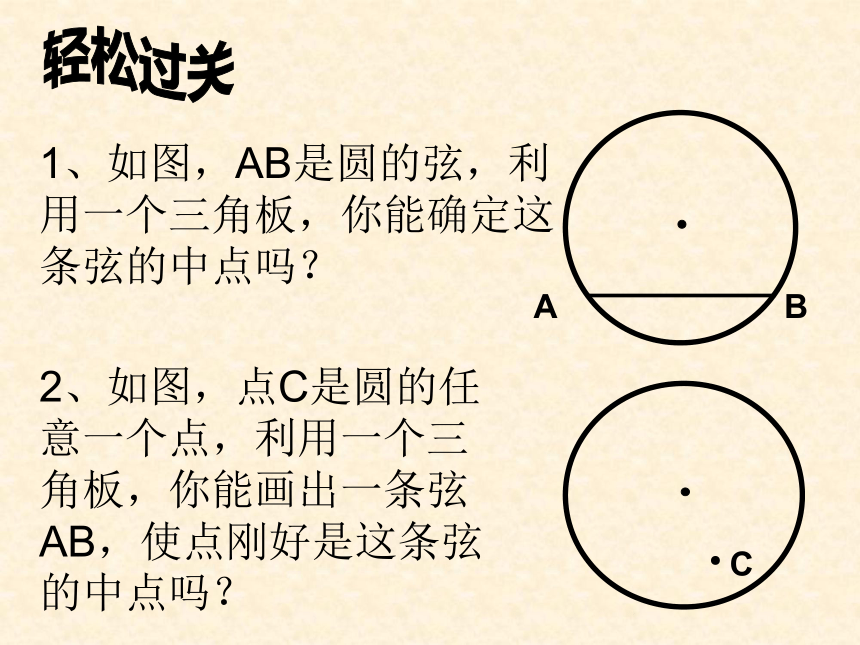
轻松过关1、如图，AB是圆的弦，利用一个三角板，你能确定这条弦的中点吗？2、如图，点C是圆的任意一个点，利用一个三角板，你能画出一条弦AB，使点刚好是这条弦的中点吗？AB●C2．如图，在⊙O中，弦
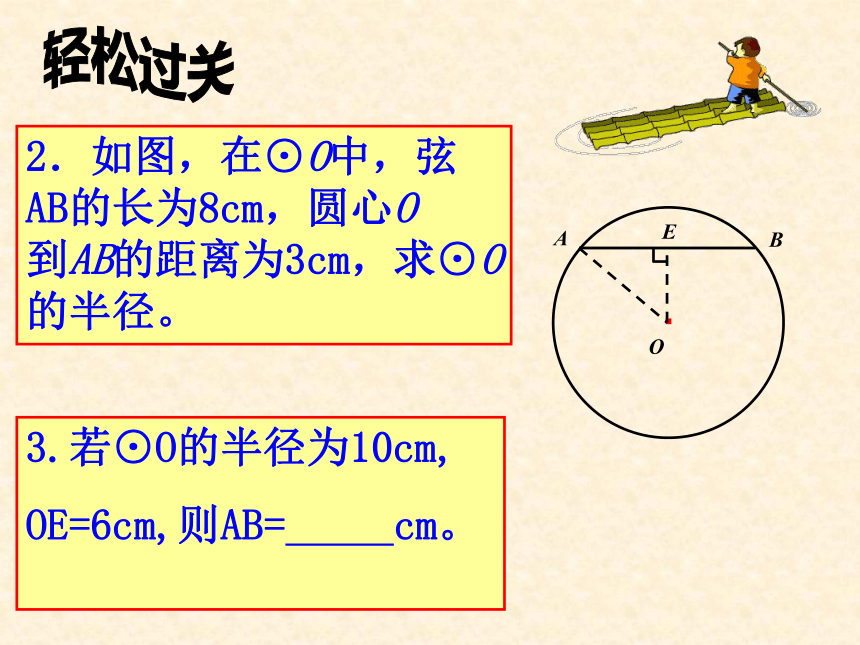
AB的长为8cm，圆心O
到AB的距离为3cm，求⊙O的半径。·OABE3.若⊙O的半径为10cm,
OE=6cm,则AB= cm。轻松过关命题（1）：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧命题（2）：弦的垂直平分线经过圆心，并且平分弦所对的两条弧C垂直于弦的直径平分这条弦，
并且平分弦所对的两条弧。推论（1） （1）平分弦（不是直径）的直径垂直于弦， 并且平分弦所对的两条弧.（2）弦的垂直平分线经过圆心，
并且平分弦所对的两条弧.垂径定理记忆根据垂径定理与推论可知对于一个圆和一条直线来说。如果具备（1）过圆心 （2）垂直于弦 （3）平分弦
（4）平分弦所对的优弧 （5）平分弦所对的劣弧上述五个量中的已知任何两个量都可推出其他三个量。注意垂径定理及推论垂直于弦的直径平分弦,并且平分弦所的两条弧.平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.弦的垂直平分线经过圆心,并且平分这条弦所对的两条弧. 垂直于弦并且平分弦所对的一条弧的直线经过圆心,并且平分弦和所对的另一条弧.平分弦并且平分弦所对的一条弧的直线经过圆心,垂直于弦,并且平分弦所对的另一条弧.平分弦所对的两条弧的直线经过圆心,并且垂直平分弦.问题 ：你知道赵州桥吗? 它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦的距离)为7.2m，你能求出赵洲桥主桥拱的半径吗？ 赵州桥主桥拱的半径是多少？ 37.4m7.2mABOCE解得：R≈27．9（m）在Rt△OAD中，由勾股定理，得即 R2=18.72+（R－7.2）2∴赵州桥的主桥拱半径约为27.9m.OA2=AD2+OD2AB=37.4，CD=7.2，OD=OC－CD=R－7.2在图中解：用 弧AB表示主桥拱，设弧AB 所在圆的圆心为O，半径为R．经过圆心O 作弦AB 的垂线OC，D为垂足，OC与AB 相交于点D，根据前面的结论，D 是AB 的中点，C是弧AB的中点，CD 就是拱高．例1 如图，已知在⊙O中，弦AB的长为8厘米，圆心O到AB的距离为3厘米，求⊙O的半径。解：连结OA。过O作OE⊥AB，垂足为E，则OE＝3厘米，AE＝BE。∵AB＝8厘米 ∴AE＝4厘米
在RtAOE中，根据勾股定理有OA＝5厘米 ∴⊙O的半径为5厘米。讲解例2 已知：如图，在以O为圆心的两个同心圆中，大圆的弦AB交小圆于C，D两点。
求证：AC＝BD。证明：过O作OE⊥AB，垂足为E，则AE＝BE，CE＝DE。
AE－CE＝BE－DE。
所以，AC＝BDE讲解讲解结论：圆的两条平行弦所夹的弧相等小 结１、圆的轴对称性
２、垂径定理及其推论的图式
小结: 解决弦时常用的辅助线：
过圆心作弦的垂线、连半径等构造直角三角形，根据垂径定理、勾股定理可解决：弦长、半径、弦心距、弓形高。