冀教版数学六年级下册-第四单元 圆柱和圆锥(有答案)
文档属性
| 名称 | 冀教版数学六年级下册-第四单元 圆柱和圆锥(有答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 175.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 10:57:46 | ||
图片预览



文档简介
单元培优测试卷
第四单元 圆柱和圆锥
一、填空。(每空2分,共32分)
1.把右图圆柱的侧面沿高剪开,展开后得到一个长方形,从而就把求圆柱侧面积(曲面面积)的问题变成了求长方形面积(平面面积)的问题。这个长方形的长等于圆柱的( ),是( ) cm;宽等于圆柱的( ),是( )cm;这个圆柱的侧面积是( )cm2。这个过程体现了转化的数学思想。
2.一个圆柱的侧面展开图是一个周长为24厘米的正方形,这个圆柱的侧面积是( )平方厘米。
3.一个圆锥的体积是76立方厘米,底面积是19平方厘米。这个圆锥的高是( )厘米。
4.爸爸送给淘气一个圆锥形陀螺,陀螺的底面直径是6厘米,高是4厘米。如果用一个长方体盒子包装它,这个盒子的容积至少是( )立方厘米。
5.一个圆柱和一个圆锥体积相同,底面积也相同,如果圆柱的高是12厘米,圆锥的高是( )厘米;如果圆锥的高是12厘米,圆柱的高是( )厘米。
6.一款牙膏出口处直径为5 mm,姐姐每次刷牙都挤出1 cm长的牙膏,一支牙膏可用36次。如果将出口处的直径改为6 mm,姐姐还是按习惯每次挤出1 cm长的牙膏,这样一支牙膏只能用( )次。
7.等底等高的圆柱和圆锥的体积相差16立方米,这个圆柱的体积是( )立方米,圆锥的体积是( )立方米。
8.如右图,把一个圆柱切成若干等份,拼成一个近似的长方体,长方体的表面积比圆柱的表面积增加了
20平方厘米,圆柱的底面周长是
6.28厘米,那么圆柱的体积是( )立方厘米。
9.把一根长是4米,底面半径是2分米的圆柱形木料截成同样长的5个小圆柱,这5个小圆柱的表面积之和比原来增加了( )平方分米。
10.如下图所示,一个小球的体积是( )立方厘米。(单位:厘米)
二、选择。(将正确答案的字母填在括号里)(每小题2分,共18分)
1.把一块圆柱形木料削成一个最大的圆锥,削去部分体积是圆锥体积的( )。
A. B. 3倍 C. D. 2倍
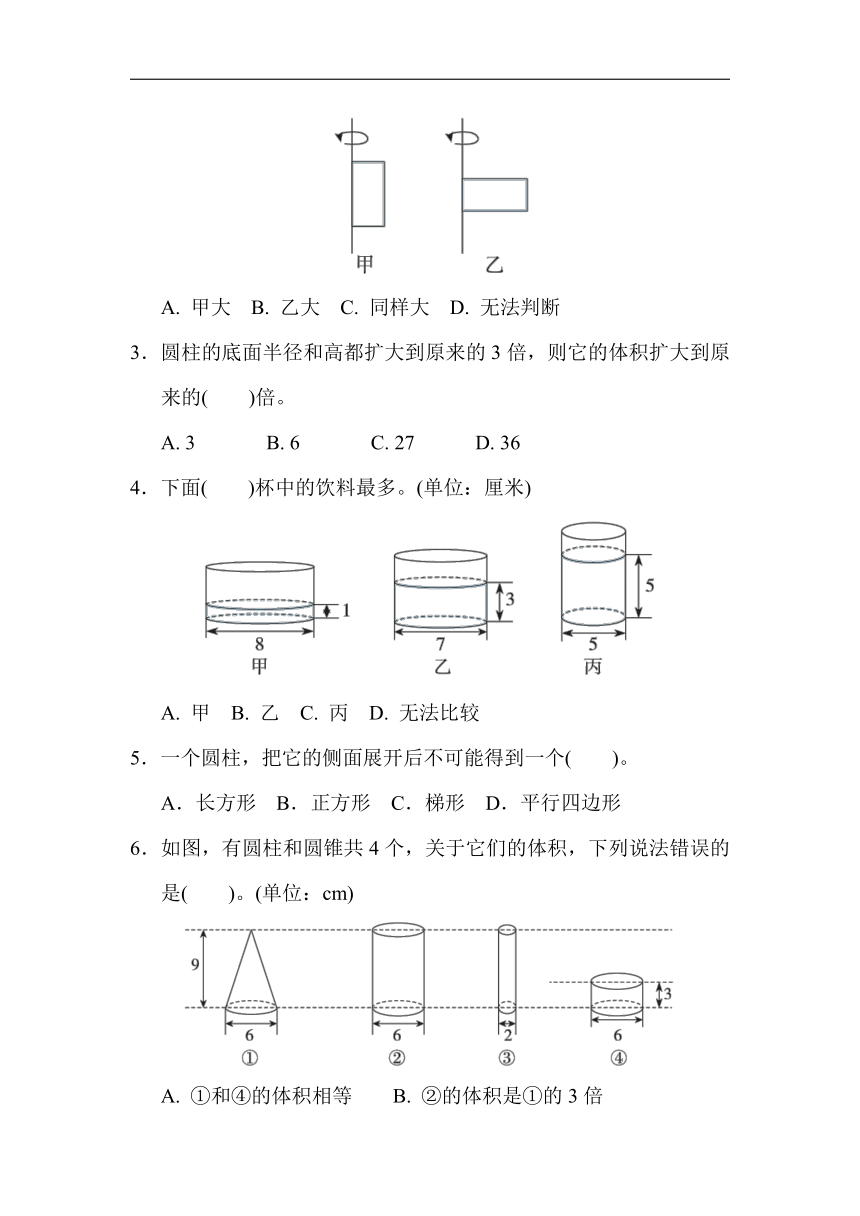
2.如图,长方形的长是4厘米,宽是2厘米,分别以长边和宽边所在的直线为轴,旋转一周可以得到两个不同的圆柱,这两个圆柱的体积相比,( )。
A. 甲大 B. 乙大 C. 同样大 D. 无法判断
3.圆柱的底面半径和高都扩大到原来的3倍,则它的体积扩大到原来的( )倍。
A. 3 B. 6 C. 27 D. 36
4.下面( )杯中的饮料最多。(单位:厘米)
A. 甲 B. 乙 C. 丙 D. 无法比较
5.一个圆柱,把它的侧面展开后不可能得到一个( )。
A.长方形 B.正方形 C.梯形 D.平行四边形
6.如图,有圆柱和圆锥共4个,关于它们的体积,下列说法错误的是( )。(单位:cm)
A. ①和④的体积相等 B. ②的体积是①的3倍
C. ②的体积是④的3倍 D. ①和③的体积相等
7.妈妈榨了一大杯橙汁招待客人(如图①),如果倒入图②所示的杯子中,那么可以倒满( )杯。(两个杯子的杯口内直径相同)
A. 3 B. 6 C. 9 D. 15
8.在一个底面直径是2分米,高是3分米的圆柱形容器里注满水,然后在水里垂直插入一根底面积是0.6平方分米,高是4分米的方钢,则溢出水的体积是( )毫升。
A. 2.4 B. 1800 C. 1.8 D. 2400
9.把底面直径是3厘米,高6 厘米的圆柱,沿底面直径切割成两个半圆柱后表面积共增加了( )平方厘米。
A. 54 B. 36 C. 18 D. 9
三、计算。(共10分)
1.求图中几何体的体积。(5分)
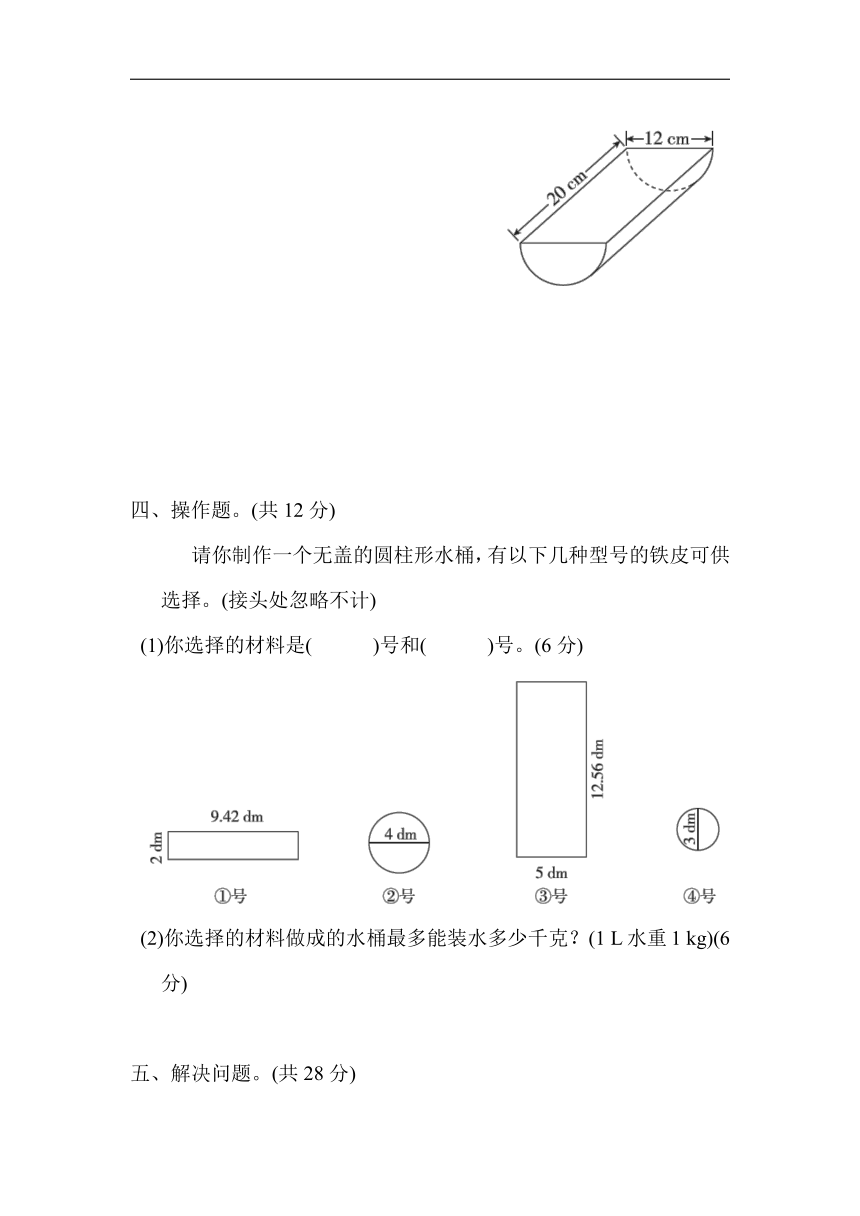
2.一个半圆柱如图所示,求它的表面积和体积。(5分)
四、操作题。(共12分)
请你制作一个无盖的圆柱形水桶,有以下几种型号的铁皮可供选择。(接头处忽略不计)
(1)你选择的材料是( )号和( )号。(6分)
(2)你选择的材料做成的水桶最多能装水多少千克?(1 L水重1 kg)(6分)
五、解决问题。(共28分)
1.压路机的前轮是圆柱形,它的宽是2米,前轮的底面半径是0.6米,如果压路机的前轮每分钟转10周,那么它10分钟压路的面积是多少平方米?(7分)
2.小明为了测量出一只乌龟的体积,按如下的步骤进行了一个实验:①小明找来一个圆柱形玻璃杯,量得底面周长是25.12 cm;②在玻璃杯中装入一定量的水,量得水面的高度是10 cm;③将乌龟放入水中完全浸没(水未溢出),再次量得水面的高度是12 cm。如果玻璃的厚度忽略不计,这只乌龟的体积大约是多少立方厘米?(7分)
3.有一堆圆锥形沙子,底面周长是12.56米,高9分米。在5米宽的公路上要铺2厘米厚的沙子,能铺多少米的公路?(7分)
4.把一块棱长是10厘米的正方体铁块熔铸成一块底面直径是20厘米的圆锥形铁块。这块圆锥形铁块的高约是多少?
解答这道题时,乐乐列出了下面的综合算式:
(10×10×10)÷ [3.14×(20÷2)2]
老师却认为是错误的,乐乐的方法错在了哪里?请用正确的方法重新列式并计算(结果保留整数)。(7分)
★附加题:天才的你,试一试。(10分)
古希腊著名的数学家阿基米德是历史上杰出的数学家之一。在他众多的科学发现中,他自己最为满意的是“圆柱容球定理”。如图,把一个球正好放在一个圆柱形容器中(容器含有上、下底),球的直径与圆柱的高和底面直径相等,此时球的体积正好是圆柱体积的,球的表面积也正好是圆柱表面积的,求出图中球的表面积和体积。
答案
一、1.底面周长 25.12 高 10 251.2
2.36 3.12
4.144
5.36 4
6.25
7.24 8
8.31.4
9.100.48
10.90 【点拨】排出水体积=2个小球的体积。
二、1.D 2.B 3.C 4.B 5.C 6.D 7.C 8.B 9.B
三、1.×3.14×(20÷2)2×3=314(m3)
1884+314=2198(m3)
2.表面积: 3.14×12×20÷2
=37.68×20÷2
=753.6÷2
=376.8(cm2)
3.14×(12÷2)2=3.14×36=113.04(cm2)
12×20=240(cm2)
376.8+113.04+240=729.84(cm2)
体积: 3.14×(12÷2)2×20÷2
=3.14×36×20÷2
=1130.4(cm3)
【点拨】半圆柱是把一个圆柱沿底面直径竖切后得到的,半圆柱的表面积就是一个长方形的面积、一个圆的面积和一个圆柱侧面积的一半的和。
四、(1)① ④(或② ③)
(2)选①号和④号:
3.14×(3÷2)2×2
=3.14×1.52×2
=14.13(dm3)
=14.13(L)
14.13×1=14.13(kg)
选②号和③号:
3.14×(4÷2)2×5
=3.14×4×5
=12.56×5
=62.8(dm3)
=62.8(L)
62.8×1=62.8(kg)
答:做成的水桶最多能装水14.13 kg或62.8 kg。
五、1.3.14×0.6×2×2×10×10=753.6(平方米)
答:它10分钟压路的面积是753.6平方米。
【点拨】压路机前轮转动1周所压路的面积就是前轮的侧面积。
2.25.12÷3.14÷2=4(cm)
3.14×42×(12-10)=100.48(cm3)
答:这只乌龟的体积大约是100.48 cm3。
3.12.56÷3.14÷2=2(米)
2厘米=0.02米
9分米=0.9米
3.14×22×0.9×÷(5×0.02)=37.68(米)
答:能铺37.68米的公路。
4.错在把正方体体积转化成圆锥体积时要除以,而这里忽略了。
÷[3.14×(20÷2)2]
=(1000×3)÷(3.14×100)
=3000÷314
≈10(厘米)
答:这块圆锥形铁块的高约是10厘米。
附加题:表面积:×[3.14×(6÷2)2×2+3.14×6×6]=113.04(cm2)
体积:×3.14×(6÷2)2×6=113.04(cm3)
答:图中球的表面积是113.04 cm2,体积是113.04 cm3。
第四单元 圆柱和圆锥
一、填空。(每空2分,共32分)
1.把右图圆柱的侧面沿高剪开,展开后得到一个长方形,从而就把求圆柱侧面积(曲面面积)的问题变成了求长方形面积(平面面积)的问题。这个长方形的长等于圆柱的( ),是( ) cm;宽等于圆柱的( ),是( )cm;这个圆柱的侧面积是( )cm2。这个过程体现了转化的数学思想。
2.一个圆柱的侧面展开图是一个周长为24厘米的正方形,这个圆柱的侧面积是( )平方厘米。
3.一个圆锥的体积是76立方厘米,底面积是19平方厘米。这个圆锥的高是( )厘米。
4.爸爸送给淘气一个圆锥形陀螺,陀螺的底面直径是6厘米,高是4厘米。如果用一个长方体盒子包装它,这个盒子的容积至少是( )立方厘米。
5.一个圆柱和一个圆锥体积相同,底面积也相同,如果圆柱的高是12厘米,圆锥的高是( )厘米;如果圆锥的高是12厘米,圆柱的高是( )厘米。
6.一款牙膏出口处直径为5 mm,姐姐每次刷牙都挤出1 cm长的牙膏,一支牙膏可用36次。如果将出口处的直径改为6 mm,姐姐还是按习惯每次挤出1 cm长的牙膏,这样一支牙膏只能用( )次。
7.等底等高的圆柱和圆锥的体积相差16立方米,这个圆柱的体积是( )立方米,圆锥的体积是( )立方米。
8.如右图,把一个圆柱切成若干等份,拼成一个近似的长方体,长方体的表面积比圆柱的表面积增加了
20平方厘米,圆柱的底面周长是
6.28厘米,那么圆柱的体积是( )立方厘米。
9.把一根长是4米,底面半径是2分米的圆柱形木料截成同样长的5个小圆柱,这5个小圆柱的表面积之和比原来增加了( )平方分米。
10.如下图所示,一个小球的体积是( )立方厘米。(单位:厘米)
二、选择。(将正确答案的字母填在括号里)(每小题2分,共18分)
1.把一块圆柱形木料削成一个最大的圆锥,削去部分体积是圆锥体积的( )。
A. B. 3倍 C. D. 2倍
2.如图,长方形的长是4厘米,宽是2厘米,分别以长边和宽边所在的直线为轴,旋转一周可以得到两个不同的圆柱,这两个圆柱的体积相比,( )。
A. 甲大 B. 乙大 C. 同样大 D. 无法判断
3.圆柱的底面半径和高都扩大到原来的3倍,则它的体积扩大到原来的( )倍。
A. 3 B. 6 C. 27 D. 36
4.下面( )杯中的饮料最多。(单位:厘米)
A. 甲 B. 乙 C. 丙 D. 无法比较
5.一个圆柱,把它的侧面展开后不可能得到一个( )。
A.长方形 B.正方形 C.梯形 D.平行四边形
6.如图,有圆柱和圆锥共4个,关于它们的体积,下列说法错误的是( )。(单位:cm)
A. ①和④的体积相等 B. ②的体积是①的3倍
C. ②的体积是④的3倍 D. ①和③的体积相等
7.妈妈榨了一大杯橙汁招待客人(如图①),如果倒入图②所示的杯子中,那么可以倒满( )杯。(两个杯子的杯口内直径相同)
A. 3 B. 6 C. 9 D. 15
8.在一个底面直径是2分米,高是3分米的圆柱形容器里注满水,然后在水里垂直插入一根底面积是0.6平方分米,高是4分米的方钢,则溢出水的体积是( )毫升。
A. 2.4 B. 1800 C. 1.8 D. 2400
9.把底面直径是3厘米,高6 厘米的圆柱,沿底面直径切割成两个半圆柱后表面积共增加了( )平方厘米。
A. 54 B. 36 C. 18 D. 9
三、计算。(共10分)
1.求图中几何体的体积。(5分)
2.一个半圆柱如图所示,求它的表面积和体积。(5分)
四、操作题。(共12分)
请你制作一个无盖的圆柱形水桶,有以下几种型号的铁皮可供选择。(接头处忽略不计)
(1)你选择的材料是( )号和( )号。(6分)
(2)你选择的材料做成的水桶最多能装水多少千克?(1 L水重1 kg)(6分)
五、解决问题。(共28分)
1.压路机的前轮是圆柱形,它的宽是2米,前轮的底面半径是0.6米,如果压路机的前轮每分钟转10周,那么它10分钟压路的面积是多少平方米?(7分)
2.小明为了测量出一只乌龟的体积,按如下的步骤进行了一个实验:①小明找来一个圆柱形玻璃杯,量得底面周长是25.12 cm;②在玻璃杯中装入一定量的水,量得水面的高度是10 cm;③将乌龟放入水中完全浸没(水未溢出),再次量得水面的高度是12 cm。如果玻璃的厚度忽略不计,这只乌龟的体积大约是多少立方厘米?(7分)
3.有一堆圆锥形沙子,底面周长是12.56米,高9分米。在5米宽的公路上要铺2厘米厚的沙子,能铺多少米的公路?(7分)
4.把一块棱长是10厘米的正方体铁块熔铸成一块底面直径是20厘米的圆锥形铁块。这块圆锥形铁块的高约是多少?
解答这道题时,乐乐列出了下面的综合算式:
(10×10×10)÷ [3.14×(20÷2)2]
老师却认为是错误的,乐乐的方法错在了哪里?请用正确的方法重新列式并计算(结果保留整数)。(7分)
★附加题:天才的你,试一试。(10分)
古希腊著名的数学家阿基米德是历史上杰出的数学家之一。在他众多的科学发现中,他自己最为满意的是“圆柱容球定理”。如图,把一个球正好放在一个圆柱形容器中(容器含有上、下底),球的直径与圆柱的高和底面直径相等,此时球的体积正好是圆柱体积的,球的表面积也正好是圆柱表面积的,求出图中球的表面积和体积。
答案
一、1.底面周长 25.12 高 10 251.2
2.36 3.12
4.144
5.36 4
6.25
7.24 8
8.31.4
9.100.48
10.90 【点拨】排出水体积=2个小球的体积。
二、1.D 2.B 3.C 4.B 5.C 6.D 7.C 8.B 9.B
三、1.×3.14×(20÷2)2×3=314(m3)
1884+314=2198(m3)
2.表面积: 3.14×12×20÷2
=37.68×20÷2
=753.6÷2
=376.8(cm2)
3.14×(12÷2)2=3.14×36=113.04(cm2)
12×20=240(cm2)
376.8+113.04+240=729.84(cm2)
体积: 3.14×(12÷2)2×20÷2
=3.14×36×20÷2
=1130.4(cm3)
【点拨】半圆柱是把一个圆柱沿底面直径竖切后得到的,半圆柱的表面积就是一个长方形的面积、一个圆的面积和一个圆柱侧面积的一半的和。
四、(1)① ④(或② ③)
(2)选①号和④号:
3.14×(3÷2)2×2
=3.14×1.52×2
=14.13(dm3)
=14.13(L)
14.13×1=14.13(kg)
选②号和③号:
3.14×(4÷2)2×5
=3.14×4×5
=12.56×5
=62.8(dm3)
=62.8(L)
62.8×1=62.8(kg)
答:做成的水桶最多能装水14.13 kg或62.8 kg。
五、1.3.14×0.6×2×2×10×10=753.6(平方米)
答:它10分钟压路的面积是753.6平方米。
【点拨】压路机前轮转动1周所压路的面积就是前轮的侧面积。
2.25.12÷3.14÷2=4(cm)
3.14×42×(12-10)=100.48(cm3)
答:这只乌龟的体积大约是100.48 cm3。
3.12.56÷3.14÷2=2(米)
2厘米=0.02米
9分米=0.9米
3.14×22×0.9×÷(5×0.02)=37.68(米)
答:能铺37.68米的公路。
4.错在把正方体体积转化成圆锥体积时要除以,而这里忽略了。
÷[3.14×(20÷2)2]
=(1000×3)÷(3.14×100)
=3000÷314
≈10(厘米)
答:这块圆锥形铁块的高约是10厘米。
附加题:表面积:×[3.14×(6÷2)2×2+3.14×6×6]=113.04(cm2)
体积:×3.14×(6÷2)2×6=113.04(cm3)
答:图中球的表面积是113.04 cm2,体积是113.04 cm3。
