2021-2022学年北师大版九年级数学下册第3章圆 期末综合复习训练(Word版含解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册第3章圆 期末综合复习训练(Word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 468.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 08:42:52 | ||
图片预览



文档简介
2021-2022学年北师大版九年级数学下册《第3章圆》期末综合复习训练(附答案)
1.下列说法,正确的是( )
A.弦是直径 B.弧是半圆
C.半圆是弧 D.过圆心的线段是直径
2.已知一定点P与圆周上点的最大距离为6cm,最小距离为2cm,则此圆的半径为( )
A.4cm B.2cm C.4cm或2cm D.8cm或4cm
3.如图是一位同学从照片上剪切下来的海上日出时的画面,“图上”太阳与海平线交于A,B两点,他测得“图上”圆的半径为10厘米,AB=16厘米.若从目前太阳所处位置到太阳完全跳出海平面的时间为16分钟,则“图上”太阳升起的速度为( )
A.1.0厘米/分 B.0.8厘米/分 C.1.2厘米/分 D.1.4厘米/分
4.⊙O的半径为5,M是圆外一点,MO=6,∠OMA=30°,则弦AB的长为( )
A.4 B.6 C.6 D.8
5.如图,AB是⊙O的直径,CD是弦,且D为中点,若∠D=30°,BC=2,则BD的值为( )
A. B. C. D.3
6.如图,四边形ABCD是圆O的内接四边形,AB为圆O的直径,若∠AOD=40°,弦AC平分∠DAB,则∠ADC=( )
A.140° B.125° C.110° D.105°
7.如图,已知平面直角坐标系内三点A(3,0)、B(5,0)、C(0,4),⊙P经过点A、B、C,则点P的坐标为( )
A.(6,8) B.(4,5) C.(4,) D.(4,)
8.如图,在扇形AOB中,OA=2,∠AOB=90°,C是OA的中点,D是的中点,连接BC,CD.则阴影部分的面积为( )
A.1 B. C. D.
9.如图,边长为4的正六边形ABCDEF的中心与坐标原点O重合,AF∥x轴,将正六边形ABCDEF绕原点O顺时针旋转n次,每次旋转60°,当n=2020时,顶点A的坐标为( )
A.(﹣2,2) B.(﹣2,﹣2) C.(2,﹣2) D.(2,2)
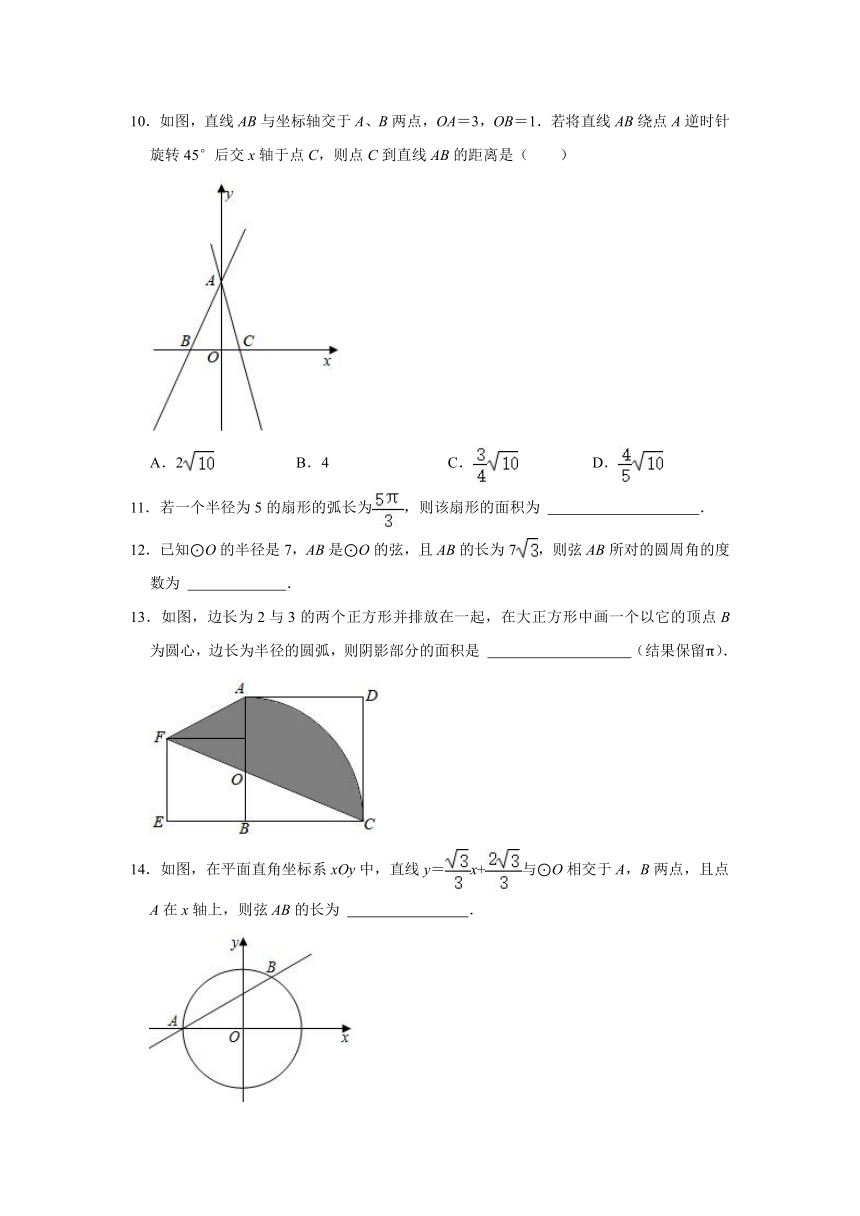
10.如图,直线AB与坐标轴交于A、B两点,OA=3,OB=1.若将直线AB绕点A逆时针旋转45°后交x轴于点C,则点C到直线AB的距离是( )
A.2 B.4 C. D.
11.若一个半径为5的扇形的弧长为,则该扇形的面积为 .
12.已知⊙O的半径是7,AB是⊙O的弦,且AB的长为7,则弦AB所对的圆周角的度数为 .
13.如图,边长为2与3的两个正方形并排放在一起,在大正方形中画一个以它的顶点B为圆心,边长为半径的圆弧,则阴影部分的面积是 (结果保留π).
14.如图,在平面直角坐标系xOy中,直线y=x+与⊙O相交于A,B两点,且点A在x轴上,则弦AB的长为 .
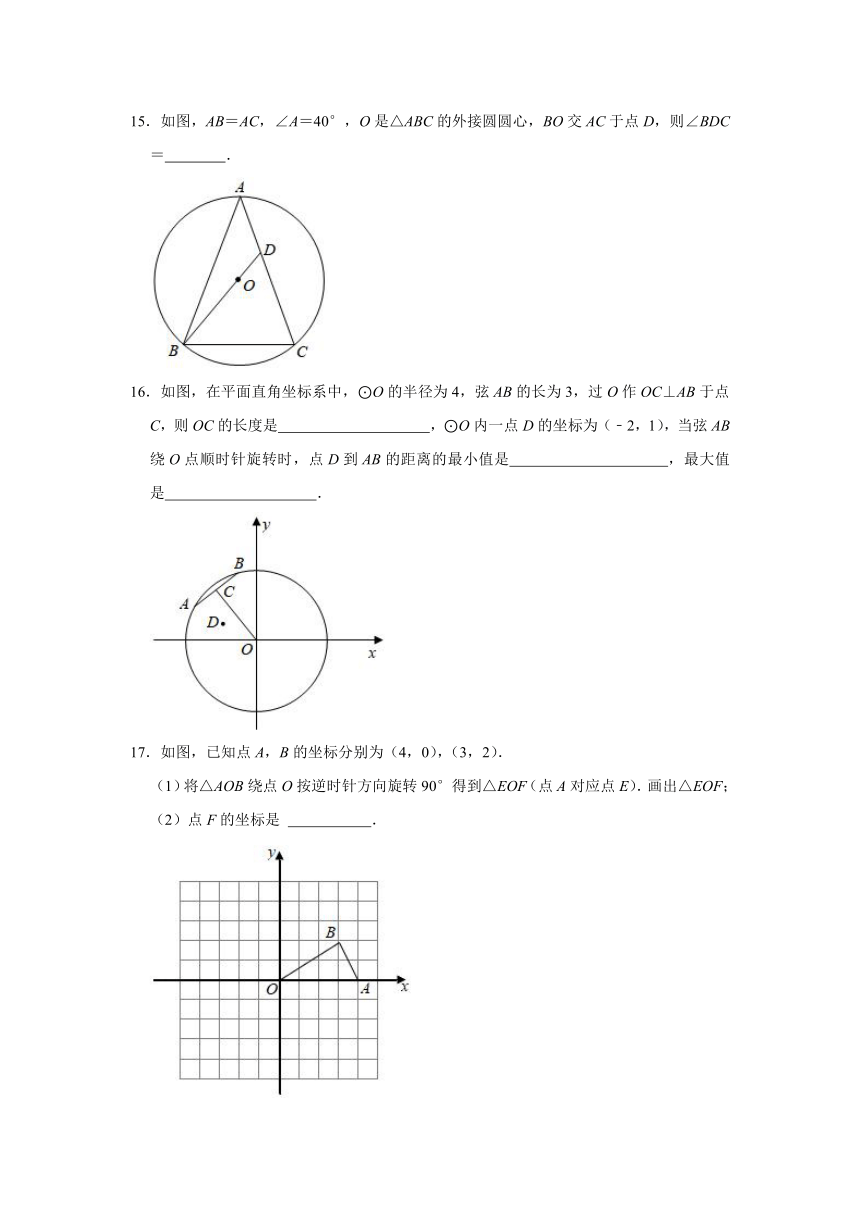
15.如图,AB=AC,∠A=40°,O是△ABC的外接圆圆心,BO交AC于点D,则∠BDC= .
16.如图,在平面直角坐标系中,⊙O的半径为4,弦AB的长为3,过O作OC⊥AB于点C,则OC的长度是 ,⊙O内一点D的坐标为(﹣2,1),当弦AB绕O点顺时针旋转时,点D到AB的距离的最小值是 ,最大值是 .
17.如图,已知点A,B的坐标分别为(4,0),(3,2).
(1)将△AOB绕点O按逆时针方向旋转90°得到△EOF(点A对应点E).画出△EOF;
(2)点F的坐标是 .
18.如图,有一座圆弧形拱桥,桥下水面宽度AB为12m,拱高CD为4m.
(1)求拱桥的半径;
(2)有一艘宽5m的货船,船舱顶部为长方形,并高出水面3.6m,求此货船是否能顺利通过拱桥?
19.如图,AB,CD为⊙O内两条相交的弦,交点为E,且AB=CD,求证:AD∥BC.
20.如图,AB为⊙O的直径,点 C、D在⊙O上,AC与OD交于点E,AE=EC,OE=ED.连接BC、CD.求证:
(1)△AOE≌△CDE;
(2)四边形OBCD是菱形.
21.如图,⊙O为△ABC的外接圆,AB为⊙O直径,AC=BC,点D在劣弧BC上,CE⊥CD交AD于E,连接BD.
(1)求证:△ACE≌△BCD.
(2)若CD=2,BD=3,求⊙O的半径.
22.如图,在⊙O中,AC为⊙O的直径,AB为⊙O的弦,点E是的中点,过点E作AB的垂线,交AB于点M,交⊙O于点N,分别连接EB,CN.
(1)EM与BE的数量关系是 ;
(2)求证:=;
(3)若AM=,MB=1,求阴影部分图形的面积.
23.如图,在△ABC中,∠BAC=90°,点F在BC边上,过A,B,F三点的⊙O交AC于另一点D,作直径AE,连接EF并延长交AC于点G,连接BE,BD,四边形BDGE是平行四边形.
(1)求证:AB=BF.
(2)当F为BC的中点,且AC=3时,求⊙O的直径长.
参考答案
1.解:A、弦是连接圆上任意两点的线段,只有经过圆心的弦才是直径,不是所有的弦都是直径.故本选项错误;
B、弧是圆上任意两点间的部分,只有直径的两个端点把圆分成的两条弧是半圆,不是所有的弧都是半圆.故本选项错误;
C、圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.所以半圆是弧是正确的.
D、过圆心的弦才是直径,不是所有过圆心的线段都是直径,故本选项错误.
故选:C.
2.解:当点P在圆内时,圆的直径为6+2=8,所以半径为4.
当点P在圆外时,圆的直径为6﹣2=4,所以半径为2.
故选:C.
3.解:设“图上”圆的圆心为O,连接OA,过点O作OD⊥AB于D,如图所示:
∵AB=16厘米,
∴AD=AB=8(厘米),
∵OA=10厘米,
∴OD===6(厘米),
∴海平线以下部分的高度=OA+OD=10+6=16(厘米),
∵太阳从所处位置到完全跳出海平面的时间为16分钟,
∴“图上”太阳升起的速度=16÷16=1.0(厘米/分),
故选:A.
4.解:过O作OC⊥AB于C,连接OA,则∠OCA=90°,
∵MO=6,∠OMA=30°,
∴OC=MO=3,
在Rt△OCA中,由勾股定理得:AC===4,
∵OC⊥AB,OC过O,
∴BC=AC,
即AB=2AC=2×4=8,
故选:D.
5.解:如图,连接AD,OC.
∵∠BOC=2∠BDC,∠BDC=30°,
∴∠BOC=60°,
∵OC=OB,
∴△BOC是等边三角形,
∴OB=BC=2,
∴AB=2OB=4,
∵D是的中点,
∴=,
∴AD=DB,
∵AB是直径,
∴∠ADB=90°,
∴BD=AB=2,
故选:A.
6.解:∵∠AOD=40°,OA=OD,
∴∠ADO=∠DAO=(180°﹣∠AOD)=70°,
∵AC平分∠DAB,
∴∠CAB=DAB=35°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠B=90°﹣∠CAB=55°,
∵四边形ABCD是⊙O的内接四边形,
∴∠ADC+∠B=180°,
∴∠ADC=180°﹣55°=125°,
故选:B.
7.解:∵⊙P经过点A、B、C,
∴点P在线段AB的垂直平分线上,
∴点P的横坐标为4,
设点P的坐标为(4,y),
作PE⊥OB于E,PF⊥OC于F,
由题意得,
=,
解得,y=,
故选:C.
8.解:连接OD,过D作DH⊥OA于H,
∵∠AOB=90°,D是的中点,
∴∠AOD=∠BOD=45°,
∵OD=OA=2,
∴DH=OD=,
∵C是OA的中点,
∴OC=1,
∴阴影部分的面积=S扇形DOB+S△CDO﹣S△BCO=+×1﹣1×2=﹣1,
故选:C.
9.解:连接OA,
∠AOH=30°,AH=2,
∴OH==2,
∵六边形ABCDEF是正六边形,
∴正六边形ABCDEF绕原点O顺时针旋转6次回到原位置,
2020÷6=336…4,
∴当n=2020时,顶点A的坐标为(﹣2,﹣2),
故选:B.
10.解:过点B作BD⊥AB,交AC于点D,过点D作DE⊥x轴于E,
∵∠BAC=45°,故△ABD为等腰直角三角形,则AB=BD,
∵∠ABC+∠BAO=90°,∠ABC+∠DBE=90°,
∴∠BAO=∠DBE,
在△AOB与△BED中,
,
∴△AOB≌△BED(AAS),
∴OA=BE=3,OB=DE=1,
∴OE=3﹣1=2,
∴点D的坐标为(2,﹣1),
设直线AC的表达式为y=kx+3,
把点D的坐标代入得2k+3=﹣1,解得k=﹣2,
∴直线AC的表达式为y=﹣2x+3,
令y=0,则﹣2x+3=0,解得x=,
∴C(,0),
∴BC=,
∵AB===,
设C点到直线AB的距离为h,
∴AB h=BC OA,
∴h===,
故选:C.
11.解:S扇形=lr=×5×=π,
故答案为π.
12.解:∠ACB和∠ADB为弦AB所对的圆周角,连接OA、OB,如图,
过O点作OH⊥AB于H,则AH=BH=AB=,
在Rt△OAH中,∵cos∠OAH===,
∴∠OAH=30°,
∵OA=OB,
∴∠OBH=∠OAH=30°,
∴∠AOB=120°,
∴∠ACB=∠AOB=60°,
∵∠ADB+∠ACB=180°,
∴∠ADB=180°﹣60°=120°,
即弦AB所对的圆周角的度数为60°或120°.
故答案为60°或120°.
13.解:如图,
∵四边形BEFH,ABCD是正方形,
∴BE=EF=2,BC=3,∠OBC=∠FEC=90°,
∵∠OCB=∠FCE,
∴△OCB∽△FCE,
∴=,
即=,
∴OB=,
∴AO=3﹣=,
∴S阴影部分=S1+S△AOF
=(S扇形ABC﹣S△BOC)+S△AOF
=(﹣××3)+××2
=,
故答案为:.
14.解:设直线AB交y轴于C,过O作OD⊥AB于D,如图:
在y=x+中,令x=0得y=,
∴C(0,),OC=,
在y=x+中令y=0得x+=0,
解得x=﹣2,
∴A(﹣2,0),OA=2,
Rt△AOC中,tan∠CAO===,
∴∠CAO=30°,
Rt△AOD中,AD=OA cos30°=2×=,
∵OD⊥AB,
∴AD=BD=,
∴AB=2,
故答案为:2.
15.解:延长BD交圆O于点G,连接CG,如图:
∵∠A=40°,
∴∠A=∠G=40°,
∵BG是⊙O的直径,
∴∠BCG=90°,
∵AB=AC,
∴∠BCA=∠CBA=(180°﹣40°)=70°,
∴∠DCG=20°,
∴∠BDC=∠G+∠DCG=40°+20°=60°,
故答案为:60°.
16.解:连接OB,
∵OC⊥AB,
∴BC=AB=,
由勾股定理得,OC==,
由勾股定理得,OD==,
当点D在直线OC上时,点D到AB的距离的最小或最大,
∴点D到AB的距离的最小值为﹣,点D到AB的距离的最大值为+,
故答案为:;﹣;+.
17.解:(1)如图,△EOF为所作;
(2)点F的坐标为(﹣2,3).
故答案为(﹣2,3).
18.解:(1)如图,设圆心为O,连接OB,OC.
∵OC⊥AB,
∴D为AB中点,
∵AB=12m,
∴BD=AB=6m.
又∵CD=4m,
设OB=OC=ON=r,则OD=(r﹣4)m.
在Rt△BOD中,根据勾股定理得:r2=(r﹣4)2+62,
解得r=6.5.
(2)连接ON.∵CD=4m,船舱顶部为长方形并高出水面AB=3.6m,
∴CE=4﹣3.6=0.4(m),
∴OE=r﹣CE=6.5﹣0.4=6.1(m),
在Rt△OEN中,EN2=ON2﹣OE2=6.52﹣6.12=5.042,
∴EN=(m).
∴MN=2EN=2×≈4.48m<5m.
∴此货船不能顺利通过这座拱桥.
19.解:∵AB=CD,
∴=,
∴﹣=﹣,
即=,
∴∠A=∠B,
∴AD∥BC.
20.证明:(1)在△AOE和△CDE中,
,
∴△AOE≌△CDE(SAS);
(2)∵△AOE≌△CDE,
∴OA=CD,∠AOE=∠D,
∴OB∥CD,
∵OA=OB,
∴OB=CD,
∴四边形OBCD为平行四边形,
∵OB=OD,
∴四边形OBCD是菱形.
21.解:(1)证明:∵AB为⊙O直径,
∴∠ACB=90°,
∵CE⊥CD,
∴∠ECD=90°,
∴∠ACE=90°﹣∠ECB=∠BCD,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(ASA);
(2)∵△ACE≌△BCD,
∴CE=CD,AE=BD,
∵CE⊥CD,
∴△ECD是等腰直角三角形,
∵CD=2,BD=3,
∴DE=2,AE=3,
∴AD=5,
∵AB为⊙O直径,
∴∠ADB=90°,
∴AB==2,
∴⊙O的半径为.
22.解:(1)∵AC为⊙O的直径,点E是的中点,
∴∠ABE=45°,
∵AB⊥EN,
∴△BME是等腰直角三角形,
∴BE=EM,
故答案为BE=EM;
(2)连接EO,
∵AC是⊙O的直径,E是的中点,
∴∠AOE=90°,
∴∠ABE=∠AOE=45°,
∵EN⊥AB,垂足为点M,
∴∠EMB=90°
∴∠ABE=∠BEN=45°,
∴=,
∵点E是的中点,
∴=,
∴=,
∴﹣=﹣,
∴=;
(3)连接AE,OB,ON,
∵EN⊥AB,垂足为点M,
∴∠AME=∠EMB=90°,
∵BM=1,由(2)得∠ABE=∠BEN=45°,
∴EM=BM=1,
又∵BE=EM,
∴BE=,
∵在Rt△AEM中,EM=1,AM=,
∴tan∠EAB==,
∴∠EAB=30°,
∵∠EAB=∠EOB,
∴∠EOB=60°,
又∵OE=OB,
∴△EOB是等边三角形,
∴OE=BE=,
又∵=,
∴BE=CN,
∴△OEB≌△OCN(SSS),
∴CN=BE=
又∵S扇形OCN==,S△OCN=CN×CN=×=,
∴S阴影=S扇形OCN﹣S△OCN=﹣.
23.解:(1)连接AF,
∵AE是⊙O的直径,
∴AF⊥EG,
∵四边形BDGE是平行四边形,
∴BD∥EG,
∴BD⊥AF,
∵∠BAC=90°,
∴BD是⊙O的直径,
∴BD垂直平分AF,
∴AB=BF;
(2)∵当F为BC的中点,
∴BF=BC,
∵AB=BF,
∴AB=BC,
∵∠BAC=90°,
∴∠C=30°,
∴∠ABC=60°,AB=AC=,
∵AB=BF,
∴∠ABD=30°,
∴BD=2,
∴⊙O的直径长为2.
1.下列说法,正确的是( )
A.弦是直径 B.弧是半圆
C.半圆是弧 D.过圆心的线段是直径
2.已知一定点P与圆周上点的最大距离为6cm,最小距离为2cm,则此圆的半径为( )
A.4cm B.2cm C.4cm或2cm D.8cm或4cm
3.如图是一位同学从照片上剪切下来的海上日出时的画面,“图上”太阳与海平线交于A,B两点,他测得“图上”圆的半径为10厘米,AB=16厘米.若从目前太阳所处位置到太阳完全跳出海平面的时间为16分钟,则“图上”太阳升起的速度为( )
A.1.0厘米/分 B.0.8厘米/分 C.1.2厘米/分 D.1.4厘米/分
4.⊙O的半径为5,M是圆外一点,MO=6,∠OMA=30°,则弦AB的长为( )
A.4 B.6 C.6 D.8
5.如图,AB是⊙O的直径,CD是弦,且D为中点,若∠D=30°,BC=2,则BD的值为( )
A. B. C. D.3
6.如图,四边形ABCD是圆O的内接四边形,AB为圆O的直径,若∠AOD=40°,弦AC平分∠DAB,则∠ADC=( )
A.140° B.125° C.110° D.105°
7.如图,已知平面直角坐标系内三点A(3,0)、B(5,0)、C(0,4),⊙P经过点A、B、C,则点P的坐标为( )
A.(6,8) B.(4,5) C.(4,) D.(4,)
8.如图,在扇形AOB中,OA=2,∠AOB=90°,C是OA的中点,D是的中点,连接BC,CD.则阴影部分的面积为( )
A.1 B. C. D.
9.如图,边长为4的正六边形ABCDEF的中心与坐标原点O重合,AF∥x轴,将正六边形ABCDEF绕原点O顺时针旋转n次,每次旋转60°,当n=2020时,顶点A的坐标为( )
A.(﹣2,2) B.(﹣2,﹣2) C.(2,﹣2) D.(2,2)
10.如图,直线AB与坐标轴交于A、B两点,OA=3,OB=1.若将直线AB绕点A逆时针旋转45°后交x轴于点C,则点C到直线AB的距离是( )
A.2 B.4 C. D.
11.若一个半径为5的扇形的弧长为,则该扇形的面积为 .
12.已知⊙O的半径是7,AB是⊙O的弦,且AB的长为7,则弦AB所对的圆周角的度数为 .
13.如图,边长为2与3的两个正方形并排放在一起,在大正方形中画一个以它的顶点B为圆心,边长为半径的圆弧,则阴影部分的面积是 (结果保留π).
14.如图,在平面直角坐标系xOy中,直线y=x+与⊙O相交于A,B两点,且点A在x轴上,则弦AB的长为 .
15.如图,AB=AC,∠A=40°,O是△ABC的外接圆圆心,BO交AC于点D,则∠BDC= .
16.如图,在平面直角坐标系中,⊙O的半径为4,弦AB的长为3,过O作OC⊥AB于点C,则OC的长度是 ,⊙O内一点D的坐标为(﹣2,1),当弦AB绕O点顺时针旋转时,点D到AB的距离的最小值是 ,最大值是 .
17.如图,已知点A,B的坐标分别为(4,0),(3,2).
(1)将△AOB绕点O按逆时针方向旋转90°得到△EOF(点A对应点E).画出△EOF;
(2)点F的坐标是 .
18.如图,有一座圆弧形拱桥,桥下水面宽度AB为12m,拱高CD为4m.
(1)求拱桥的半径;
(2)有一艘宽5m的货船,船舱顶部为长方形,并高出水面3.6m,求此货船是否能顺利通过拱桥?
19.如图,AB,CD为⊙O内两条相交的弦,交点为E,且AB=CD,求证:AD∥BC.
20.如图,AB为⊙O的直径,点 C、D在⊙O上,AC与OD交于点E,AE=EC,OE=ED.连接BC、CD.求证:
(1)△AOE≌△CDE;
(2)四边形OBCD是菱形.
21.如图,⊙O为△ABC的外接圆,AB为⊙O直径,AC=BC,点D在劣弧BC上,CE⊥CD交AD于E,连接BD.
(1)求证:△ACE≌△BCD.
(2)若CD=2,BD=3,求⊙O的半径.
22.如图,在⊙O中,AC为⊙O的直径,AB为⊙O的弦,点E是的中点,过点E作AB的垂线,交AB于点M,交⊙O于点N,分别连接EB,CN.
(1)EM与BE的数量关系是 ;
(2)求证:=;
(3)若AM=,MB=1,求阴影部分图形的面积.
23.如图,在△ABC中,∠BAC=90°,点F在BC边上,过A,B,F三点的⊙O交AC于另一点D,作直径AE,连接EF并延长交AC于点G,连接BE,BD,四边形BDGE是平行四边形.
(1)求证:AB=BF.
(2)当F为BC的中点,且AC=3时,求⊙O的直径长.
参考答案
1.解:A、弦是连接圆上任意两点的线段,只有经过圆心的弦才是直径,不是所有的弦都是直径.故本选项错误;
B、弧是圆上任意两点间的部分,只有直径的两个端点把圆分成的两条弧是半圆,不是所有的弧都是半圆.故本选项错误;
C、圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.所以半圆是弧是正确的.
D、过圆心的弦才是直径,不是所有过圆心的线段都是直径,故本选项错误.
故选:C.
2.解:当点P在圆内时,圆的直径为6+2=8,所以半径为4.
当点P在圆外时,圆的直径为6﹣2=4,所以半径为2.
故选:C.
3.解:设“图上”圆的圆心为O,连接OA,过点O作OD⊥AB于D,如图所示:
∵AB=16厘米,
∴AD=AB=8(厘米),
∵OA=10厘米,
∴OD===6(厘米),
∴海平线以下部分的高度=OA+OD=10+6=16(厘米),
∵太阳从所处位置到完全跳出海平面的时间为16分钟,
∴“图上”太阳升起的速度=16÷16=1.0(厘米/分),
故选:A.
4.解:过O作OC⊥AB于C,连接OA,则∠OCA=90°,
∵MO=6,∠OMA=30°,
∴OC=MO=3,
在Rt△OCA中,由勾股定理得:AC===4,
∵OC⊥AB,OC过O,
∴BC=AC,
即AB=2AC=2×4=8,
故选:D.
5.解:如图,连接AD,OC.
∵∠BOC=2∠BDC,∠BDC=30°,
∴∠BOC=60°,
∵OC=OB,
∴△BOC是等边三角形,
∴OB=BC=2,
∴AB=2OB=4,
∵D是的中点,
∴=,
∴AD=DB,
∵AB是直径,
∴∠ADB=90°,
∴BD=AB=2,
故选:A.
6.解:∵∠AOD=40°,OA=OD,
∴∠ADO=∠DAO=(180°﹣∠AOD)=70°,
∵AC平分∠DAB,
∴∠CAB=DAB=35°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠B=90°﹣∠CAB=55°,
∵四边形ABCD是⊙O的内接四边形,
∴∠ADC+∠B=180°,
∴∠ADC=180°﹣55°=125°,
故选:B.
7.解:∵⊙P经过点A、B、C,
∴点P在线段AB的垂直平分线上,
∴点P的横坐标为4,
设点P的坐标为(4,y),
作PE⊥OB于E,PF⊥OC于F,
由题意得,
=,
解得,y=,
故选:C.
8.解:连接OD,过D作DH⊥OA于H,
∵∠AOB=90°,D是的中点,
∴∠AOD=∠BOD=45°,
∵OD=OA=2,
∴DH=OD=,
∵C是OA的中点,
∴OC=1,
∴阴影部分的面积=S扇形DOB+S△CDO﹣S△BCO=+×1﹣1×2=﹣1,
故选:C.
9.解:连接OA,
∠AOH=30°,AH=2,
∴OH==2,
∵六边形ABCDEF是正六边形,
∴正六边形ABCDEF绕原点O顺时针旋转6次回到原位置,
2020÷6=336…4,
∴当n=2020时,顶点A的坐标为(﹣2,﹣2),
故选:B.
10.解:过点B作BD⊥AB,交AC于点D,过点D作DE⊥x轴于E,
∵∠BAC=45°,故△ABD为等腰直角三角形,则AB=BD,
∵∠ABC+∠BAO=90°,∠ABC+∠DBE=90°,
∴∠BAO=∠DBE,
在△AOB与△BED中,
,
∴△AOB≌△BED(AAS),
∴OA=BE=3,OB=DE=1,
∴OE=3﹣1=2,
∴点D的坐标为(2,﹣1),
设直线AC的表达式为y=kx+3,
把点D的坐标代入得2k+3=﹣1,解得k=﹣2,
∴直线AC的表达式为y=﹣2x+3,
令y=0,则﹣2x+3=0,解得x=,
∴C(,0),
∴BC=,
∵AB===,
设C点到直线AB的距离为h,
∴AB h=BC OA,
∴h===,
故选:C.
11.解:S扇形=lr=×5×=π,
故答案为π.
12.解:∠ACB和∠ADB为弦AB所对的圆周角,连接OA、OB,如图,
过O点作OH⊥AB于H,则AH=BH=AB=,
在Rt△OAH中,∵cos∠OAH===,
∴∠OAH=30°,
∵OA=OB,
∴∠OBH=∠OAH=30°,
∴∠AOB=120°,
∴∠ACB=∠AOB=60°,
∵∠ADB+∠ACB=180°,
∴∠ADB=180°﹣60°=120°,
即弦AB所对的圆周角的度数为60°或120°.
故答案为60°或120°.
13.解:如图,
∵四边形BEFH,ABCD是正方形,
∴BE=EF=2,BC=3,∠OBC=∠FEC=90°,
∵∠OCB=∠FCE,
∴△OCB∽△FCE,
∴=,
即=,
∴OB=,
∴AO=3﹣=,
∴S阴影部分=S1+S△AOF
=(S扇形ABC﹣S△BOC)+S△AOF
=(﹣××3)+××2
=,
故答案为:.
14.解:设直线AB交y轴于C,过O作OD⊥AB于D,如图:
在y=x+中,令x=0得y=,
∴C(0,),OC=,
在y=x+中令y=0得x+=0,
解得x=﹣2,
∴A(﹣2,0),OA=2,
Rt△AOC中,tan∠CAO===,
∴∠CAO=30°,
Rt△AOD中,AD=OA cos30°=2×=,
∵OD⊥AB,
∴AD=BD=,
∴AB=2,
故答案为:2.
15.解:延长BD交圆O于点G,连接CG,如图:
∵∠A=40°,
∴∠A=∠G=40°,
∵BG是⊙O的直径,
∴∠BCG=90°,
∵AB=AC,
∴∠BCA=∠CBA=(180°﹣40°)=70°,
∴∠DCG=20°,
∴∠BDC=∠G+∠DCG=40°+20°=60°,
故答案为:60°.
16.解:连接OB,
∵OC⊥AB,
∴BC=AB=,
由勾股定理得,OC==,
由勾股定理得,OD==,
当点D在直线OC上时,点D到AB的距离的最小或最大,
∴点D到AB的距离的最小值为﹣,点D到AB的距离的最大值为+,
故答案为:;﹣;+.
17.解:(1)如图,△EOF为所作;
(2)点F的坐标为(﹣2,3).
故答案为(﹣2,3).
18.解:(1)如图,设圆心为O,连接OB,OC.
∵OC⊥AB,
∴D为AB中点,
∵AB=12m,
∴BD=AB=6m.
又∵CD=4m,
设OB=OC=ON=r,则OD=(r﹣4)m.
在Rt△BOD中,根据勾股定理得:r2=(r﹣4)2+62,
解得r=6.5.
(2)连接ON.∵CD=4m,船舱顶部为长方形并高出水面AB=3.6m,
∴CE=4﹣3.6=0.4(m),
∴OE=r﹣CE=6.5﹣0.4=6.1(m),
在Rt△OEN中,EN2=ON2﹣OE2=6.52﹣6.12=5.042,
∴EN=(m).
∴MN=2EN=2×≈4.48m<5m.
∴此货船不能顺利通过这座拱桥.
19.解:∵AB=CD,
∴=,
∴﹣=﹣,
即=,
∴∠A=∠B,
∴AD∥BC.
20.证明:(1)在△AOE和△CDE中,
,
∴△AOE≌△CDE(SAS);
(2)∵△AOE≌△CDE,
∴OA=CD,∠AOE=∠D,
∴OB∥CD,
∵OA=OB,
∴OB=CD,
∴四边形OBCD为平行四边形,
∵OB=OD,
∴四边形OBCD是菱形.
21.解:(1)证明:∵AB为⊙O直径,
∴∠ACB=90°,
∵CE⊥CD,
∴∠ECD=90°,
∴∠ACE=90°﹣∠ECB=∠BCD,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(ASA);
(2)∵△ACE≌△BCD,
∴CE=CD,AE=BD,
∵CE⊥CD,
∴△ECD是等腰直角三角形,
∵CD=2,BD=3,
∴DE=2,AE=3,
∴AD=5,
∵AB为⊙O直径,
∴∠ADB=90°,
∴AB==2,
∴⊙O的半径为.
22.解:(1)∵AC为⊙O的直径,点E是的中点,
∴∠ABE=45°,
∵AB⊥EN,
∴△BME是等腰直角三角形,
∴BE=EM,
故答案为BE=EM;
(2)连接EO,
∵AC是⊙O的直径,E是的中点,
∴∠AOE=90°,
∴∠ABE=∠AOE=45°,
∵EN⊥AB,垂足为点M,
∴∠EMB=90°
∴∠ABE=∠BEN=45°,
∴=,
∵点E是的中点,
∴=,
∴=,
∴﹣=﹣,
∴=;
(3)连接AE,OB,ON,
∵EN⊥AB,垂足为点M,
∴∠AME=∠EMB=90°,
∵BM=1,由(2)得∠ABE=∠BEN=45°,
∴EM=BM=1,
又∵BE=EM,
∴BE=,
∵在Rt△AEM中,EM=1,AM=,
∴tan∠EAB==,
∴∠EAB=30°,
∵∠EAB=∠EOB,
∴∠EOB=60°,
又∵OE=OB,
∴△EOB是等边三角形,
∴OE=BE=,
又∵=,
∴BE=CN,
∴△OEB≌△OCN(SSS),
∴CN=BE=
又∵S扇形OCN==,S△OCN=CN×CN=×=,
∴S阴影=S扇形OCN﹣S△OCN=﹣.
23.解:(1)连接AF,
∵AE是⊙O的直径,
∴AF⊥EG,
∵四边形BDGE是平行四边形,
∴BD∥EG,
∴BD⊥AF,
∵∠BAC=90°,
∴BD是⊙O的直径,
∴BD垂直平分AF,
∴AB=BF;
(2)∵当F为BC的中点,
∴BF=BC,
∵AB=BF,
∴AB=BC,
∵∠BAC=90°,
∴∠C=30°,
∴∠ABC=60°,AB=AC=,
∵AB=BF,
∴∠ABD=30°,
∴BD=2,
∴⊙O的直径长为2.
