人教版 初中数学九年级上册24.3正多边形和圆 课件(共26张PPT)
文档属性
| 名称 | 人教版 初中数学九年级上册24.3正多边形和圆 课件(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-23 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
一、复习旧知
1.n边形的内角和公式是__________.
2.n边形的外角和等于_______.
3.正多边形的定义:
(n-2) ●180°
360°
各边相等、各角也相等的多边形是正多边形.
二、情景导入
三、 讲授新知
(一)正多边形与圆的关系
正多边形和圆的关系非常密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.
B
E
C
D
A
O
F
如图, 把⊙O分成相等的5段弧,依次连接各分点得到正五边形ABCDE.
·
A
B
C
D
E
O
又 五边形ABCDE的顶点都在⊙O上,
∴ 五边形ABCDE是⊙O的内接正五边形, ⊙O是五边形ABCDE的外接圆.
以圆内接正五边形为例证明
⌒
⌒
⌒
⌒
⌒
同理∠B =∠C =∠D =∠E.
∴ AB=BC=CD=DE=EA,
∴ ∠A=∠B.
EA
DE
D
C
AB
=
=
=
=
C
B
Q
⌒
⌒
⌒
AB
DA
BCE
3
C
=
=
,
.
(二)正多边形与圆的有关概念
正多边形的中心:正多边形的外接圆的圆心.
正多边形的半径:外接圆的半径.
正多边形的中心角:
正多边形的每一条边所对的圆心角.
正多边形的边心距:
中心到正多边形的一边的距离.
O
·
中心角
半径R
边心距r
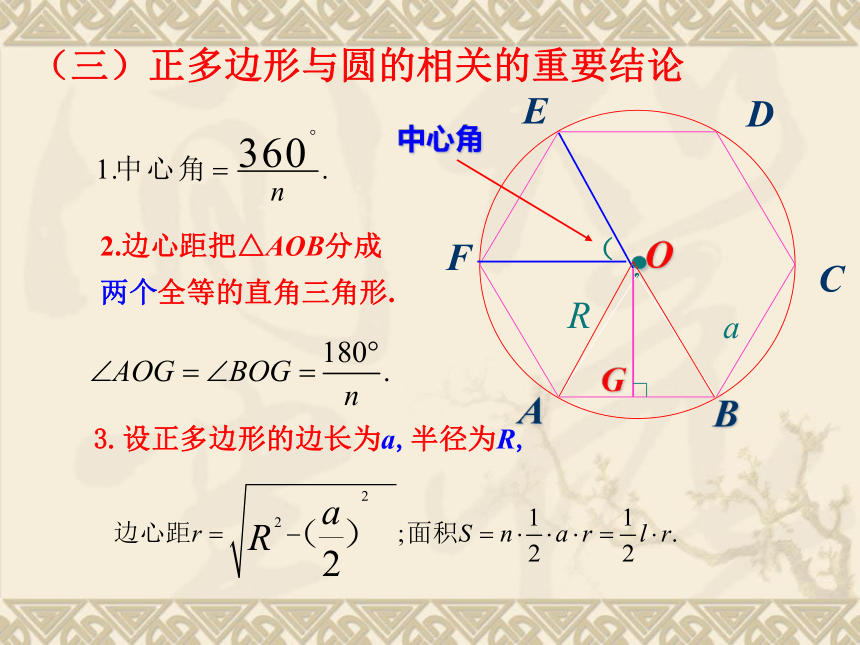
(三)正多边形与圆的相关的重要结论
中心角
2.边心距把△AOB分成
两个全等的直角三角形.
3.设正多边形的边长为a,半径为R,
E
F
C
D
.
.
O
A
B
G
R
a
(
4.正n边形的一个内角的度数是____________;
中心角是___________;
5.正多边形的中心角与外角的大小关系是_______.
相等
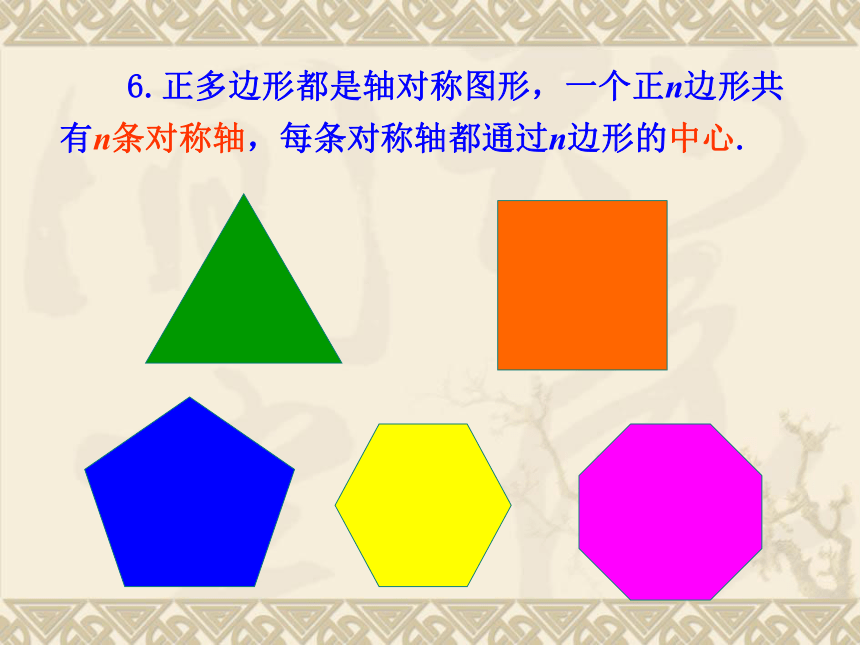
6.正多边形都是轴对称图形,一个正n边形共有n条对称轴,每条对称轴都通过n边形的中心.
注意: 边数是偶数的正多边形还是中心对称图形,它的中心就是对称中心.
例 已知正六边形ABCDEF的半径为R,求这个正六边
形的边长、周长P6和面积S6.
解:作半径OA、OB;作OG⊥AB,
垂足为G,得Rt△OGB.
∵∠GOB= ,
∴a6 =2·Rsin30°=R,
∴P6=6·a6=6R,
∵r6=Rcos30°= ,
∴
(四)典例解析
(五)正多边形的画法
画正多边形的基本原理是等分圆周.
具体地说,一是使用量角器等分圆心角,从而等分圆周,顺次连结各分点,就等到正多边形.
作半径为R的正n边形.
依据:在同圆中,相等的圆心角所对的弧相等.画法:作相等的圆心角可以等分圆.
二是使用尺规等分圆周,顺次连结各分点,就等到正多边形.
画正四、八边形.
只要作出已知⊙O的互相垂直的直径即得圆内接正方形,再过圆心作各边的垂线与⊙O相交,或作各中心角的角平分线与⊙O相交,即得圆接正八边形,照此方法依次可作正十六边形、正三十二边形、正六十四边形……
画正六、三、十二边形
以半径长在圆周上截取六段相等的弧,依次连接各等分点,则作出正六边形.
先作出正六边形,则可作正三角形,正十二边形,正二十四边形………
A
B
C
D
N
正五角形的尺规画法
已知半径为R的⊙A,用多种工具多种方法作出圆内接正三角形.
A
探索之旅
画法一:1.用量角器画圆心角∠DAB=1200,∠BAC=1200. 2.连接CB、BD、DC,则△BCD为圆内接正三角形.
3.连接CD、DE、EC,则△CDE为圆内接正三角形.
画法三:1.作直径AD;
2.以A为圆心,以OA为半径画弧,交⊙O于B,C.
3.连接DB,BC,CD,则△BCD为圆内接正三角形.
O
C
D
A
B
1.下列说法中正确的是( C )
A.各边都相等的多边形是正多边形
B.正多边形既是轴对称图形,又是中心对称图形
C.各边都相等的圆内接多边形是正多边形
D.各角都相等的圆内接多边形是正多边形
随堂演练
2.如果一个正多边形的中心角为72°,那么这个正多边
形的边数是( B )
A.4 B.5 C.6 D.7
3.如果一个正多边形的每个外角都等于36°,则这个多边形的中心角等于( A )
A.36° B.18° C.72° D.54°
4.如图,点O是正六边形的对称中心,如果用一副三角板的角,借助点O(使直角的顶点落在点O处),把这个正六边形的面积n等分,那么n的所有可能
取值的个数是( B )
A.4 B.5 C.6 D.7
5.如图,正六边形的内切圆的半径OD= cm,则它的
中心角∠AOB=________,边长AB=______cm,
正六边形的面积S=________cm2.
60°
2
6.如图,要拧开一个边长为a=6mm的正六边形螺帽,扳手张开的开口b至少为多少?
解:如图,∠ABC=120°. AB=BC=a, AC=b.
过B作BD⊥AC于点D,
则AD=DC= b.
在Rt△ABD中,∠BAC=30°,
∴BD= AB=3mm.
∴b=2AD=6 mm.
即扳手张开的开口b至少要 6 mm.
A
C
B D
归纳总结
1.正多边形和圆的有关概念.
2.正多边形和圆的重要结论.
3.正多边形的画法.
一、复习旧知
1.n边形的内角和公式是__________.
2.n边形的外角和等于_______.
3.正多边形的定义:
(n-2) ●180°
360°
各边相等、各角也相等的多边形是正多边形.
二、情景导入
三、 讲授新知
(一)正多边形与圆的关系
正多边形和圆的关系非常密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.
B
E
C
D
A
O
F
如图, 把⊙O分成相等的5段弧,依次连接各分点得到正五边形ABCDE.
·
A
B
C
D
E
O
又 五边形ABCDE的顶点都在⊙O上,
∴ 五边形ABCDE是⊙O的内接正五边形, ⊙O是五边形ABCDE的外接圆.
以圆内接正五边形为例证明
⌒
⌒
⌒
⌒
⌒
同理∠B =∠C =∠D =∠E.
∴ AB=BC=CD=DE=EA,
∴ ∠A=∠B.
EA
DE
D
C
AB
=
=
=
=
C
B
Q
⌒
⌒
⌒
AB
DA
BCE
3
C
=
=
,
.
(二)正多边形与圆的有关概念
正多边形的中心:正多边形的外接圆的圆心.
正多边形的半径:外接圆的半径.
正多边形的中心角:
正多边形的每一条边所对的圆心角.
正多边形的边心距:
中心到正多边形的一边的距离.
O
·
中心角
半径R
边心距r
(三)正多边形与圆的相关的重要结论
中心角
2.边心距把△AOB分成
两个全等的直角三角形.
3.设正多边形的边长为a,半径为R,
E
F
C
D
.
.
O
A
B
G
R
a
(
4.正n边形的一个内角的度数是____________;
中心角是___________;
5.正多边形的中心角与外角的大小关系是_______.
相等
6.正多边形都是轴对称图形,一个正n边形共有n条对称轴,每条对称轴都通过n边形的中心.
注意: 边数是偶数的正多边形还是中心对称图形,它的中心就是对称中心.
例 已知正六边形ABCDEF的半径为R,求这个正六边
形的边长、周长P6和面积S6.
解:作半径OA、OB;作OG⊥AB,
垂足为G,得Rt△OGB.
∵∠GOB= ,
∴a6 =2·Rsin30°=R,
∴P6=6·a6=6R,
∵r6=Rcos30°= ,
∴
(四)典例解析
(五)正多边形的画法
画正多边形的基本原理是等分圆周.
具体地说,一是使用量角器等分圆心角,从而等分圆周,顺次连结各分点,就等到正多边形.
作半径为R的正n边形.
依据:在同圆中,相等的圆心角所对的弧相等.画法:作相等的圆心角可以等分圆.
二是使用尺规等分圆周,顺次连结各分点,就等到正多边形.
画正四、八边形.
只要作出已知⊙O的互相垂直的直径即得圆内接正方形,再过圆心作各边的垂线与⊙O相交,或作各中心角的角平分线与⊙O相交,即得圆接正八边形,照此方法依次可作正十六边形、正三十二边形、正六十四边形……
画正六、三、十二边形
以半径长在圆周上截取六段相等的弧,依次连接各等分点,则作出正六边形.
先作出正六边形,则可作正三角形,正十二边形,正二十四边形………
A
B
C
D
N
正五角形的尺规画法
已知半径为R的⊙A,用多种工具多种方法作出圆内接正三角形.
A
探索之旅
画法一:1.用量角器画圆心角∠DAB=1200,∠BAC=1200. 2.连接CB、BD、DC,则△BCD为圆内接正三角形.
3.连接CD、DE、EC,则△CDE为圆内接正三角形.
画法三:1.作直径AD;
2.以A为圆心,以OA为半径画弧,交⊙O于B,C.
3.连接DB,BC,CD,则△BCD为圆内接正三角形.
O
C
D
A
B
1.下列说法中正确的是( C )
A.各边都相等的多边形是正多边形
B.正多边形既是轴对称图形,又是中心对称图形
C.各边都相等的圆内接多边形是正多边形
D.各角都相等的圆内接多边形是正多边形
随堂演练
2.如果一个正多边形的中心角为72°,那么这个正多边
形的边数是( B )
A.4 B.5 C.6 D.7
3.如果一个正多边形的每个外角都等于36°,则这个多边形的中心角等于( A )
A.36° B.18° C.72° D.54°
4.如图,点O是正六边形的对称中心,如果用一副三角板的角,借助点O(使直角的顶点落在点O处),把这个正六边形的面积n等分,那么n的所有可能
取值的个数是( B )
A.4 B.5 C.6 D.7
5.如图,正六边形的内切圆的半径OD= cm,则它的
中心角∠AOB=________,边长AB=______cm,
正六边形的面积S=________cm2.
60°
2
6.如图,要拧开一个边长为a=6mm的正六边形螺帽,扳手张开的开口b至少为多少?
解:如图,∠ABC=120°. AB=BC=a, AC=b.
过B作BD⊥AC于点D,
则AD=DC= b.
在Rt△ABD中,∠BAC=30°,
∴BD= AB=3mm.
∴b=2AD=6 mm.
即扳手张开的开口b至少要 6 mm.
A
C
B D
归纳总结
1.正多边形和圆的有关概念.
2.正多边形和圆的重要结论.
3.正多边形的画法.
同课章节目录
