北师大版八年级上册第一章勾股定理导学案(共3课时)
文档属性
| 名称 | 北师大版八年级上册第一章勾股定理导学案(共3课时) |  | |
| 格式 | zip | ||
| 文件大小 | 238.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-27 07:00:56 | ||
图片预览

文档简介
第一章 勾股定理
1.1、探索勾股定理学习提纲(1)
备课人:张红、张瑜
学习目标:
1、用数格子(或割、补、拼等)的办法体验勾股定理的探索过程
2、理解勾股定理反映的直角三角形的三边之间的数量关系
3、会初步运用勾股定理进行简单的计算和实际运用.
课前自学∶
1、三角形的三边关系:
2.等腰三角形的边关系
3.等边三角形的边关系
4.直角三角形有什么特点
探究新课:
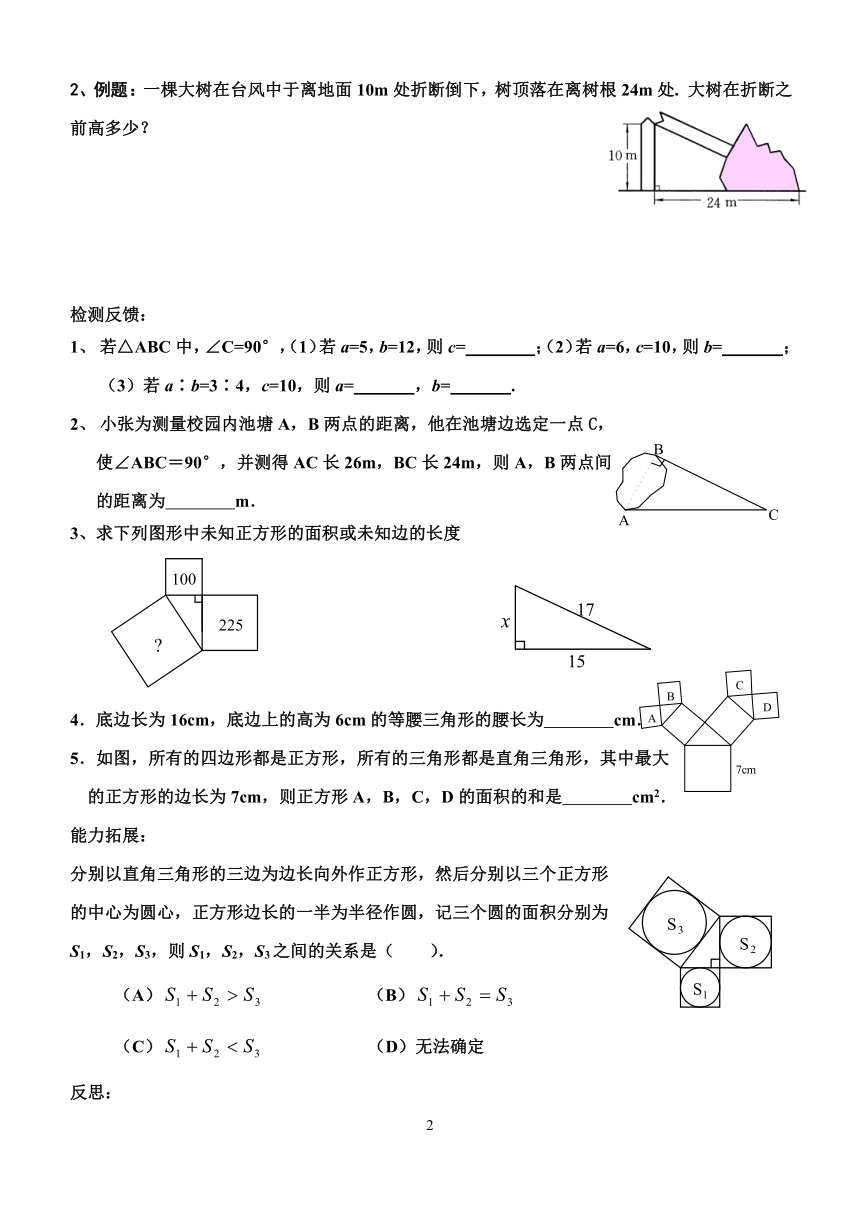
1、观察下面两幅图,填表:
A的面积
(单位面积)
B的面积
(单位面积)
C的面积
(单位面积)
左图
右图
(1)如果直角三角形的两直角边为a、b,斜边为c,用直角三角形的边长来表示上图中正方形的面积
(2)分别以5厘米、12厘米为直角边作出一个直角三角形,并测量斜边的长度.上述规律对这个三角形仍然成立吗?分别以3厘米、4厘米为直角边作出一个直角三角形呢?
(3)直角三角形三边之间存在的关系:
2、例题:一棵大树在台风中于离地面10m处折断倒下,树顶落在离树根24m处. 大树在折断之前高多少?
检测反馈:
若△ABC中,∠C=90°,(1)若a=5,b=12,则c= ;(2)若a=6,c=10,则b= ;(3)若a∶b=3∶4,c=10,则a= ,b= .
小张为测量校园内池塘A,B两点的距离,他在池塘边选定一点C,
使∠ABC=90°,并测得AC长26m,BC长24m,则A,B两点间
的距离为 m.
3、求下列图形中未知正方形的面积或未知边的长度
4.底边长为16cm,底边上的高为6cm的等腰三角形的腰长为 cm.
5.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大
的正方形的边长为7cm,则正方形A,B,C,D的面积的和是 cm2.
能力拓展:
分别以直角三角形的三边为边长向外作正方形,然后分别以三个正方形
的中心为圆心,正方形边长的一半为半径作圆,记三个圆的面积分别为
S1,S2,S3,则S1,S2,S3之间的关系是( ).
(A) (B)
(C) (D)无法确定
反思:
1.1、探索勾股定理学习提纲(2)
备课人:张红、张瑜
学习目标:
1、进一步掌握勾股定理
2、利用图形的面积来验证勾股定理
3、会运用勾股定理解决实际问题.
课前自学∶
(1)勾股定理的内容是
(2)直角三角形两边长为3和4,求第三边长
探究新课:验证勾股定理
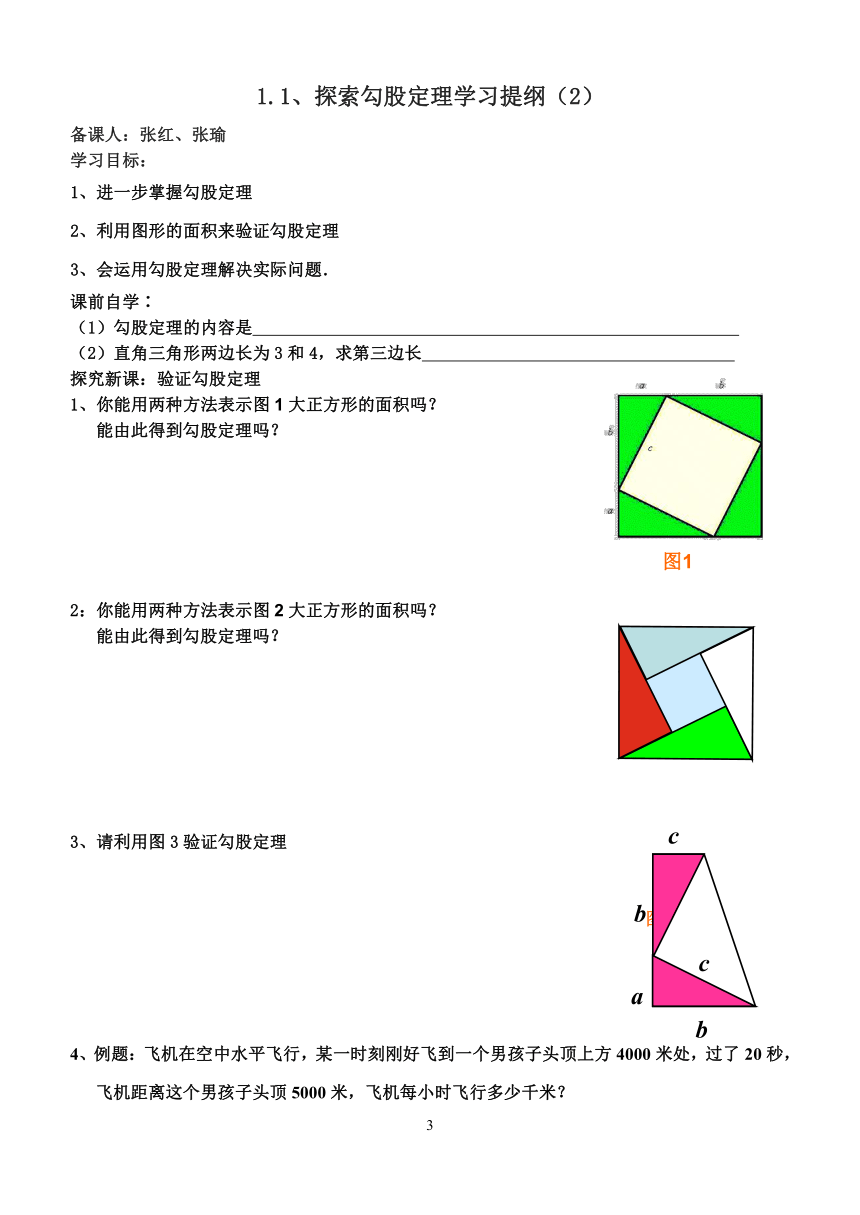
1、你能用两种方法表示图1大正方形的面积吗?
能由此得到勾股定理吗?
2:你能用两种方法表示图2大正方形的面积吗?
能由此得到勾股定理吗?
3、请利用图3验证勾股定理
图3
4、例题:飞机在空中水平飞行,某一时刻刚好飞到一个男孩子头顶上方4000米处,过了20秒,飞机距离这个男孩子头顶5000米,飞机每小时飞行多少千米?
检测反馈:
1.某农舍的大门是一个木制的矩形栅栏,它的高为2m,宽为1.5m,现需要在相对的顶点间用一块木棒加固,木板的长为 .
2.直角三角形两直角边长分别为5cm,12cm,则斜边上的高为 .
3.等腰三角形的腰长为13cm,底边长为10cm,则面积为( ).
A.30 cm2 B.130 cm2 C.120 cm2 D.60 cm2
4.暑假中,小明和同学们到某海岛去探宝旅游,按照如图所示的
路线探宝. 他们登陆后先往东走8km,又往北走2km,遇到障
碍后又往西走3km,再折向北走6km处往东一拐,仅走1km
就找到了宝藏,则登陆点到埋宝藏点的直线距离为 km.
能力拓展:
1.已知直角△ABC的两直角边分别为6,8,分别以其三边为直径作半圆,求图中阴影部分的面积.
2.有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它恰好落在斜边AB上,且与AE重合,求CD的长.
反思:
1.2、能得到直角三角形吗学习提纲
备课人:张红、张瑜
学习目标:
1、掌握勾股定理的逆定理及常用勾股数
2、会判断给出的三条边能否围成直角三角形
3、会运用勾股定理及其逆定理解决实际问题.
课前自学∶
(1)勾股定理的内容是
(2)勾股定理的逆定理内容是
探究新课:
分别以下面几组数为边长作三角形:
(1)3,4,5 (2)5,12,13 (3)8,15,17
用量角器量一量,你作出的三角形是直角三角形吗?
如何判断哪个角是直角呢?
勾股数:
常用勾股数:
说明:(1)勾股数的整数倍仍然为勾股数;
(2)以勾股数的倍数为三边长的三角形一定是直角三角形。
3、例题:已知AB⊥BC,AB=4,BC=3,CD=13,AD=12;求四边形ABCD的面积.
检测反馈:
1、下列几组数中能作为直角三角形的三边长度的是________________.
① 9、12、15 ② 15、39、36 ③ 6、5、4 ④ 22、18、12
2、如果△ABC中的三边长满足,则△ABC的面积是 。
3、如下图,在方格纸上画了一个△ABC,试判断△ABC是否为直角三角形,说明理由.
4、已知、、是△ABC的三条边,依据下列条件,判断△ABC是否为直角三角形?若是,指出直角。
(1);
(2);
(3)(均为正数);
能力拓展:
已知中,,
求AC边上的高线的长。
若一个三角形的三边长分别为(其中为整数),则当=_________时,
这个三角形是直角三角形.
在直线上依次摆着七个正方形,已知斜放的三个正方形的面积是1,2,3,正放着的四个正方形
的面积依次是则的值是多少.
反思:
1.1、探索勾股定理学习提纲(1)
备课人:张红、张瑜
学习目标:
1、用数格子(或割、补、拼等)的办法体验勾股定理的探索过程
2、理解勾股定理反映的直角三角形的三边之间的数量关系
3、会初步运用勾股定理进行简单的计算和实际运用.
课前自学∶
1、三角形的三边关系:
2.等腰三角形的边关系
3.等边三角形的边关系
4.直角三角形有什么特点
探究新课:
1、观察下面两幅图,填表:
A的面积
(单位面积)
B的面积
(单位面积)
C的面积
(单位面积)
左图
右图
(1)如果直角三角形的两直角边为a、b,斜边为c,用直角三角形的边长来表示上图中正方形的面积
(2)分别以5厘米、12厘米为直角边作出一个直角三角形,并测量斜边的长度.上述规律对这个三角形仍然成立吗?分别以3厘米、4厘米为直角边作出一个直角三角形呢?
(3)直角三角形三边之间存在的关系:
2、例题:一棵大树在台风中于离地面10m处折断倒下,树顶落在离树根24m处. 大树在折断之前高多少?
检测反馈:
若△ABC中,∠C=90°,(1)若a=5,b=12,则c= ;(2)若a=6,c=10,则b= ;(3)若a∶b=3∶4,c=10,则a= ,b= .
小张为测量校园内池塘A,B两点的距离,他在池塘边选定一点C,
使∠ABC=90°,并测得AC长26m,BC长24m,则A,B两点间
的距离为 m.
3、求下列图形中未知正方形的面积或未知边的长度
4.底边长为16cm,底边上的高为6cm的等腰三角形的腰长为 cm.
5.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大
的正方形的边长为7cm,则正方形A,B,C,D的面积的和是 cm2.
能力拓展:
分别以直角三角形的三边为边长向外作正方形,然后分别以三个正方形
的中心为圆心,正方形边长的一半为半径作圆,记三个圆的面积分别为
S1,S2,S3,则S1,S2,S3之间的关系是( ).
(A) (B)
(C) (D)无法确定
反思:
1.1、探索勾股定理学习提纲(2)
备课人:张红、张瑜
学习目标:
1、进一步掌握勾股定理
2、利用图形的面积来验证勾股定理
3、会运用勾股定理解决实际问题.
课前自学∶
(1)勾股定理的内容是
(2)直角三角形两边长为3和4,求第三边长
探究新课:验证勾股定理
1、你能用两种方法表示图1大正方形的面积吗?
能由此得到勾股定理吗?
2:你能用两种方法表示图2大正方形的面积吗?
能由此得到勾股定理吗?
3、请利用图3验证勾股定理
图3
4、例题:飞机在空中水平飞行,某一时刻刚好飞到一个男孩子头顶上方4000米处,过了20秒,飞机距离这个男孩子头顶5000米,飞机每小时飞行多少千米?
检测反馈:
1.某农舍的大门是一个木制的矩形栅栏,它的高为2m,宽为1.5m,现需要在相对的顶点间用一块木棒加固,木板的长为 .
2.直角三角形两直角边长分别为5cm,12cm,则斜边上的高为 .
3.等腰三角形的腰长为13cm,底边长为10cm,则面积为( ).
A.30 cm2 B.130 cm2 C.120 cm2 D.60 cm2
4.暑假中,小明和同学们到某海岛去探宝旅游,按照如图所示的
路线探宝. 他们登陆后先往东走8km,又往北走2km,遇到障
碍后又往西走3km,再折向北走6km处往东一拐,仅走1km
就找到了宝藏,则登陆点到埋宝藏点的直线距离为 km.
能力拓展:
1.已知直角△ABC的两直角边分别为6,8,分别以其三边为直径作半圆,求图中阴影部分的面积.
2.有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它恰好落在斜边AB上,且与AE重合,求CD的长.
反思:
1.2、能得到直角三角形吗学习提纲
备课人:张红、张瑜
学习目标:
1、掌握勾股定理的逆定理及常用勾股数
2、会判断给出的三条边能否围成直角三角形
3、会运用勾股定理及其逆定理解决实际问题.
课前自学∶
(1)勾股定理的内容是
(2)勾股定理的逆定理内容是
探究新课:
分别以下面几组数为边长作三角形:
(1)3,4,5 (2)5,12,13 (3)8,15,17
用量角器量一量,你作出的三角形是直角三角形吗?
如何判断哪个角是直角呢?
勾股数:
常用勾股数:
说明:(1)勾股数的整数倍仍然为勾股数;
(2)以勾股数的倍数为三边长的三角形一定是直角三角形。
3、例题:已知AB⊥BC,AB=4,BC=3,CD=13,AD=12;求四边形ABCD的面积.
检测反馈:
1、下列几组数中能作为直角三角形的三边长度的是________________.
① 9、12、15 ② 15、39、36 ③ 6、5、4 ④ 22、18、12
2、如果△ABC中的三边长满足,则△ABC的面积是 。
3、如下图,在方格纸上画了一个△ABC,试判断△ABC是否为直角三角形,说明理由.
4、已知、、是△ABC的三条边,依据下列条件,判断△ABC是否为直角三角形?若是,指出直角。
(1);
(2);
(3)(均为正数);
能力拓展:
已知中,,
求AC边上的高线的长。
若一个三角形的三边长分别为(其中为整数),则当=_________时,
这个三角形是直角三角形.
在直线上依次摆着七个正方形,已知斜放的三个正方形的面积是1,2,3,正放着的四个正方形
的面积依次是则的值是多少.
反思:
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
