华东师大版数学八年级上册 第13章 全等三角形 复习(课件)(共22张PPT)
文档属性
| 名称 | 华东师大版数学八年级上册 第13章 全等三角形 复习(课件)(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 332.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
第13章 全等三角形 复习课件
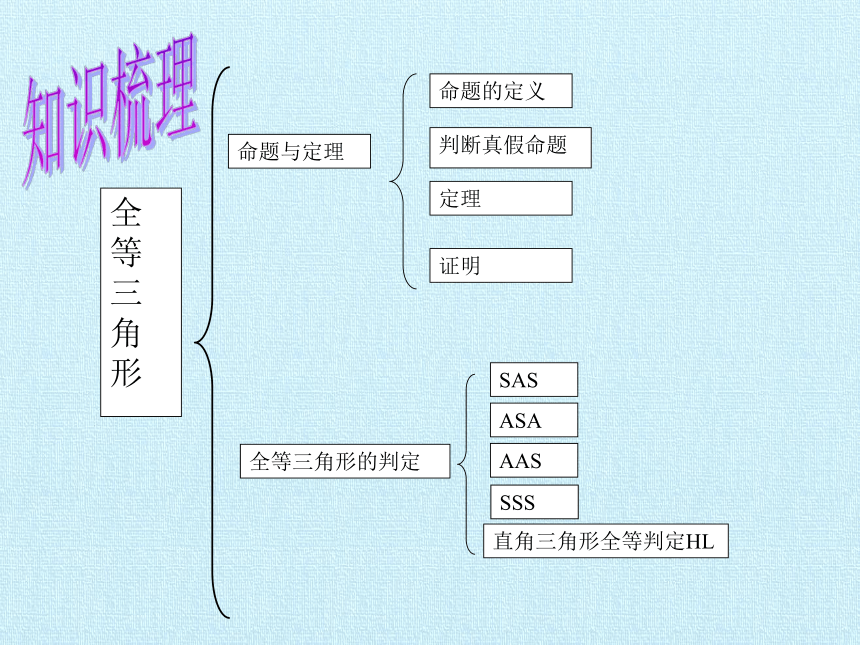
命题与定理
全等三角形的判定
SAS
ASA
AAS
SSS
直角三角形全等判定HL
全
等
三
角
形
知识梳理
命题的定义
判断真假命题
定理
证明
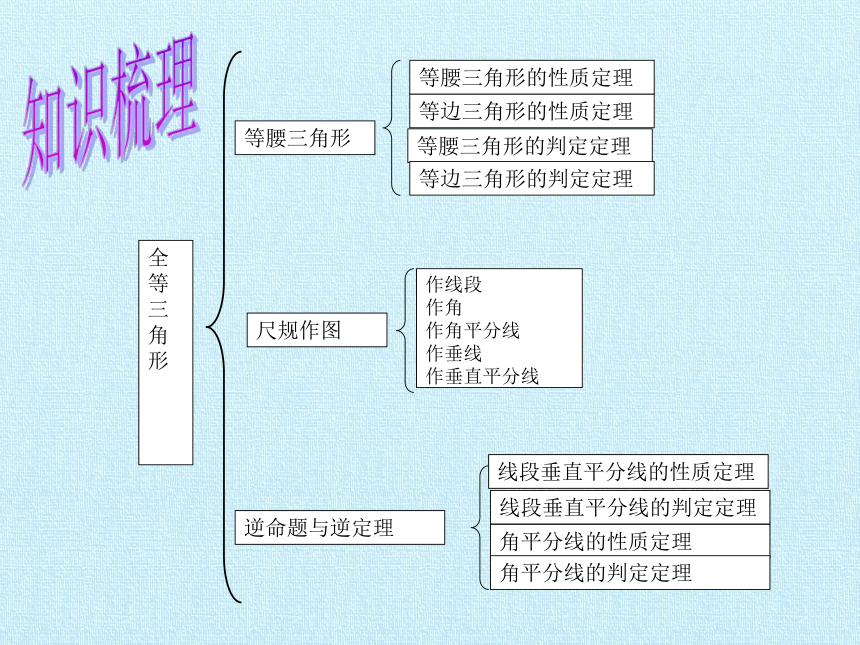
等腰三角形
等边三角形的性质定理
等腰三角形的性质定理
等腰三角形的判定定理
等边三角形的判定定理
尺规作图
作线段
作角
作角平分线
作垂线
作垂直平分线
逆命题与逆定理
线段垂直平分线的性质定理
线段垂直平分线的判定定理
角平分线的性质定理
角平分线的判定定理
全
等
三
角
形
知识梳理
复习指导一
复习时间:2分钟
复习方法:独立看书,独立思考。
复习要求:
熟记命题的概念以及命题的构成。
1.指出下列命题中的真命题和假命题:
(1)同位角相等,两直线平行;
(2)多边形的内角和等于是180°;
(3)如果两个三角形有两条边和一个角相等,那么这两个三角形一定全等。
(真命题)
(假命题)
(假命题)
复习检测一:
复习指导二
复习时间:3分钟
复习方法:独立看书,独立思考。
复习要求:
能说出全等三角形性质及五种判定。
1.这节课复习的判定两个三角形全等的方法?
2.如图,AB垂直 BE于点B,DE垂直 BE于点E,
(1)若AB=DE,BC=EF, 则 ABC与 DEF ,
根据是 。
(2)若 A= D,AB=DE,则 ABC与 DEF ,
根据是 。
(3)若 A= D,BC=EF, 则 ABC与 DEF ,
根据是 。
SAS,ASA,AAS,SSS,HL
AAS
ASA
SAS
复习检测二
复习指导三
复习时间:2分钟
复习方法:独立看书,独立思考。
复习要求:能说出等腰三角形的性质判定 并进行相关计算。
⒈等腰三角形一个底角为75°,它的另外两个角为:
75°, 30°
70°,40°或55°,55°
35°,35°
⒉等腰三角形一个角为70°,它的另外两个角为:
3.等腰三角形一个角为110°,它的另外两个角为:
① 顶角+2×底角=180°
② 顶角=180°-2×底角
③ 底角=(180°-顶角)÷2
④ 0°<顶角<180°
⑤ 0°<底角<90°
归纳:在等腰三角形中,
复习检测三
4.已知:如图, 在△ABC中, AB=AC。D是BC边上的中点,∠B=300,求:(1)∠ADC的大小;(2)∠1的大小。
A
B
D
C
=1800-30°-90°=60°
∴∠1=1800-∠B-∠ADB(等式的性质)。
∵ ∠B=30°(已知)
解:(1)
∵AB=AC,BD=CD(已知)
∴AB⊥BC(三线合一)
(2)
∴∠ADC=∠ADB= 90°
∵∠1+∠B+∠ADB=180°(三角形内角和定理)
5.如图,AB∥CD,∠1=∠2,
求证::AB=AC
A
B
C
D
1
2
分析:
要证AB=AC,
可设法证明∠B=∠2 ,
而∠1=∠2 ,
因此只要证明∠B=∠2 ,
你能写出证明过程吗?
而已知AB∥CD,从而可证。
复习指导四
复习时间:2分钟
复习方法:独立看书,独立思考。
复习要求:能熟练说出尺规作图的作法。
1.如图是求作已知线段的中点的尺规作图,把作法补充完整:
作法:分别以 、 为圆心,大于 的长为半径作弧,两弧交于 、 两点,连结 交AB于 ,则点 就是线段AB的中点。
复习检测四
A
B
AB的一半
C
D
CD
M
M
2.已知: ∠AOB。
利用尺规作:∠A'O'B'
使∠A'O'B'=2∠AOB。
B
O
A
作法一:
C
A’
B’
∠A'O'B'为所求。
B
O
A
法二:
C
D
C’
E
B’
O’
A
∠A'O'B'为所求。
复习指导五
复习时间:3分钟
复习方法:独立看书,独立思考。
复习要求:会用线段垂直平分线、角平分线的性质和判定的进行相关计算。
1.说出下列命题的逆命题,并判定逆命题的真假:
①既是中心对称,又是轴对称的图形是圆。
②有一组对边平行且相等的四边形是平行四边形。
③磁悬浮列车是一种高速行驶时不接触地面的交通工具。
逆命题:圆既是中心对称,又是轴对称的图形——真命题。
逆命题:平行四边形有一组对边平行并且相等——真命题。
逆命题:高速行驶时,不接触地面的交通工具是磁悬浮列车——假命题。
复习检测五
2.如图,△ABC中,∠C=90°,∠BAC的平分线交BC于点D,若CD=4,则点D到AB的距离是多少?
解:过点D作DE⊥AB于点E,
∵AD是∠BAC的平分线,
∠ C=90° DE⊥AB
∴DE=CD
∵CD=4
∴DE=4
【解析】
过点D作DE⊥AB于点E,然后根据角平分线上的点到角的两边距离相等可得DE=CD,即可得解。
E
3.如图, AD是∠BAC的平分线, DE⊥AB ,DF⊥AC, 垂足分别为E、F,连结EF,EF与AD交于点G,求证:AD垂直平分EF。
证明:∵ AD是∠BAC的平分线, DE⊥AB ,DF⊥AC
∴DE=DF(角平分线上的点到角两边的距离相等)
由直角三角形全等的判定定理HL得:
△AED≌△AFD∴AE=AF
在△AEG和△AFG中,
AE=AF,∠EAG=∠FAG,AG=AG
∴ △AEG≌△AFG
∴∠AGE=∠AGF=90°
∴AD垂直于EF
∴AD垂直平分EF
知识归纳易错点:
1.学生不能正确理解角平分线的性质及其判定,常忽略“到角两边的距离”的要求而导致出错。
2.要分清垂直平分线与原线段的关系,不要误认为原线段垂直平分垂直平分线。
A
D
N
E
B
F
M
C
1.已知:BD⊥AM于点D,CE⊥AN于点E,
BD,CE交点F,CF=BF,
求证:点F在∠A的平分线上。
提示:
证明△CDF≌△BEF。
利用角平分线的判定定理说明结论。
当堂训练
2.△ABC中,AB>AC ,∠A的平分线与BC的垂直平分线DM相交于D,过D作DE ⊥AB于E,作DF⊥AC于F,求证:BE=CF。
A
B
C
D
E
F
M
提示:
连接BD、CD,利用线段的垂直平分线的性质可得BD=CD;
利用角平分线的性质证明DE=DC;
利用HL判定△DMB≌△DMC,从而可得BE=CF。
谢 谢
第13章 全等三角形 复习课件
命题与定理
全等三角形的判定
SAS
ASA
AAS
SSS
直角三角形全等判定HL
全
等
三
角
形
知识梳理
命题的定义
判断真假命题
定理
证明
等腰三角形
等边三角形的性质定理
等腰三角形的性质定理
等腰三角形的判定定理
等边三角形的判定定理
尺规作图
作线段
作角
作角平分线
作垂线
作垂直平分线
逆命题与逆定理
线段垂直平分线的性质定理
线段垂直平分线的判定定理
角平分线的性质定理
角平分线的判定定理
全
等
三
角
形
知识梳理
复习指导一
复习时间:2分钟
复习方法:独立看书,独立思考。
复习要求:
熟记命题的概念以及命题的构成。
1.指出下列命题中的真命题和假命题:
(1)同位角相等,两直线平行;
(2)多边形的内角和等于是180°;
(3)如果两个三角形有两条边和一个角相等,那么这两个三角形一定全等。
(真命题)
(假命题)
(假命题)
复习检测一:
复习指导二
复习时间:3分钟
复习方法:独立看书,独立思考。
复习要求:
能说出全等三角形性质及五种判定。
1.这节课复习的判定两个三角形全等的方法?
2.如图,AB垂直 BE于点B,DE垂直 BE于点E,
(1)若AB=DE,BC=EF, 则 ABC与 DEF ,
根据是 。
(2)若 A= D,AB=DE,则 ABC与 DEF ,
根据是 。
(3)若 A= D,BC=EF, 则 ABC与 DEF ,
根据是 。
SAS,ASA,AAS,SSS,HL
AAS
ASA
SAS
复习检测二
复习指导三
复习时间:2分钟
复习方法:独立看书,独立思考。
复习要求:能说出等腰三角形的性质判定 并进行相关计算。
⒈等腰三角形一个底角为75°,它的另外两个角为:
75°, 30°
70°,40°或55°,55°
35°,35°
⒉等腰三角形一个角为70°,它的另外两个角为:
3.等腰三角形一个角为110°,它的另外两个角为:
① 顶角+2×底角=180°
② 顶角=180°-2×底角
③ 底角=(180°-顶角)÷2
④ 0°<顶角<180°
⑤ 0°<底角<90°
归纳:在等腰三角形中,
复习检测三
4.已知:如图, 在△ABC中, AB=AC。D是BC边上的中点,∠B=300,求:(1)∠ADC的大小;(2)∠1的大小。
A
B
D
C
=1800-30°-90°=60°
∴∠1=1800-∠B-∠ADB(等式的性质)。
∵ ∠B=30°(已知)
解:(1)
∵AB=AC,BD=CD(已知)
∴AB⊥BC(三线合一)
(2)
∴∠ADC=∠ADB= 90°
∵∠1+∠B+∠ADB=180°(三角形内角和定理)
5.如图,AB∥CD,∠1=∠2,
求证::AB=AC
A
B
C
D
1
2
分析:
要证AB=AC,
可设法证明∠B=∠2 ,
而∠1=∠2 ,
因此只要证明∠B=∠2 ,
你能写出证明过程吗?
而已知AB∥CD,从而可证。
复习指导四
复习时间:2分钟
复习方法:独立看书,独立思考。
复习要求:能熟练说出尺规作图的作法。
1.如图是求作已知线段的中点的尺规作图,把作法补充完整:
作法:分别以 、 为圆心,大于 的长为半径作弧,两弧交于 、 两点,连结 交AB于 ,则点 就是线段AB的中点。
复习检测四
A
B
AB的一半
C
D
CD
M
M
2.已知: ∠AOB。
利用尺规作:∠A'O'B'
使∠A'O'B'=2∠AOB。
B
O
A
作法一:
C
A’
B’
∠A'O'B'为所求。
B
O
A
法二:
C
D
C’
E
B’
O’
A
∠A'O'B'为所求。
复习指导五
复习时间:3分钟
复习方法:独立看书,独立思考。
复习要求:会用线段垂直平分线、角平分线的性质和判定的进行相关计算。
1.说出下列命题的逆命题,并判定逆命题的真假:
①既是中心对称,又是轴对称的图形是圆。
②有一组对边平行且相等的四边形是平行四边形。
③磁悬浮列车是一种高速行驶时不接触地面的交通工具。
逆命题:圆既是中心对称,又是轴对称的图形——真命题。
逆命题:平行四边形有一组对边平行并且相等——真命题。
逆命题:高速行驶时,不接触地面的交通工具是磁悬浮列车——假命题。
复习检测五
2.如图,△ABC中,∠C=90°,∠BAC的平分线交BC于点D,若CD=4,则点D到AB的距离是多少?
解:过点D作DE⊥AB于点E,
∵AD是∠BAC的平分线,
∠ C=90° DE⊥AB
∴DE=CD
∵CD=4
∴DE=4
【解析】
过点D作DE⊥AB于点E,然后根据角平分线上的点到角的两边距离相等可得DE=CD,即可得解。
E
3.如图, AD是∠BAC的平分线, DE⊥AB ,DF⊥AC, 垂足分别为E、F,连结EF,EF与AD交于点G,求证:AD垂直平分EF。
证明:∵ AD是∠BAC的平分线, DE⊥AB ,DF⊥AC
∴DE=DF(角平分线上的点到角两边的距离相等)
由直角三角形全等的判定定理HL得:
△AED≌△AFD∴AE=AF
在△AEG和△AFG中,
AE=AF,∠EAG=∠FAG,AG=AG
∴ △AEG≌△AFG
∴∠AGE=∠AGF=90°
∴AD垂直于EF
∴AD垂直平分EF
知识归纳易错点:
1.学生不能正确理解角平分线的性质及其判定,常忽略“到角两边的距离”的要求而导致出错。
2.要分清垂直平分线与原线段的关系,不要误认为原线段垂直平分垂直平分线。
A
D
N
E
B
F
M
C
1.已知:BD⊥AM于点D,CE⊥AN于点E,
BD,CE交点F,CF=BF,
求证:点F在∠A的平分线上。
提示:
证明△CDF≌△BEF。
利用角平分线的判定定理说明结论。
当堂训练
2.△ABC中,AB>AC ,∠A的平分线与BC的垂直平分线DM相交于D,过D作DE ⊥AB于E,作DF⊥AC于F,求证:BE=CF。
A
B
C
D
E
F
M
提示:
连接BD、CD,利用线段的垂直平分线的性质可得BD=CD;
利用角平分线的性质证明DE=DC;
利用HL判定△DMB≌△DMC,从而可得BE=CF。
谢 谢
