华东师大版数学八年级上册 14.2 勾股定理的应用 第三课时 课件(共12张PPT)
文档属性
| 名称 | 华东师大版数学八年级上册 14.2 勾股定理的应用 第三课时 课件(共12张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 199.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-23 22:13:52 | ||
图片预览


文档简介
(共12张PPT)
勾股定理的应用(三)
例1. 蚂议最短路程问题.
(1) 如图所示。有一个圆柱,它的高等于12厘米,底面半径等于3厘米。在圆柱下底面的A点有一只蚂蚁,它想吃到上底面的A点相对的B点处的事物,沿着圆柱侧面需要爬行的最短路程是多少?
(п的值取3)
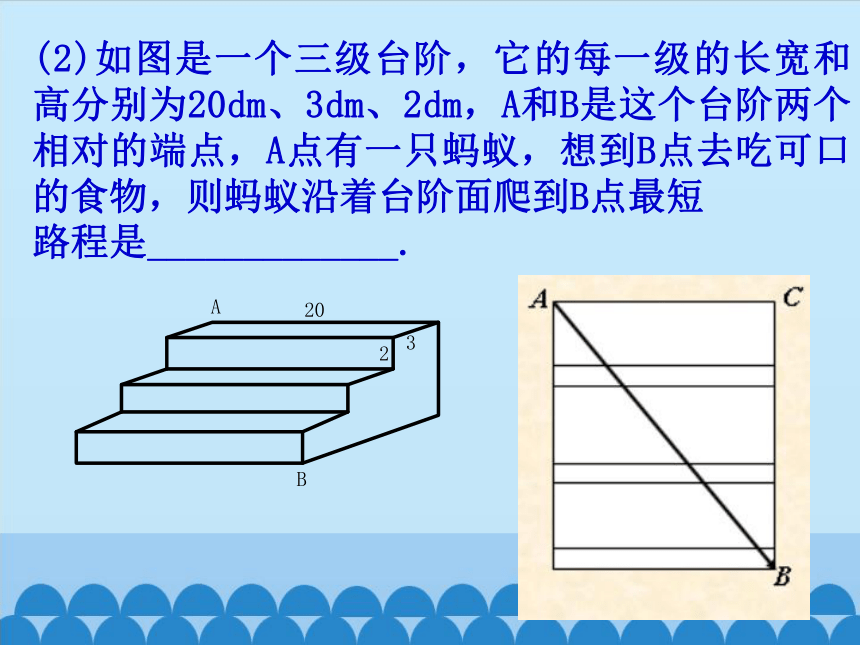
(2)如图是一个三级台阶,它的每一级的长宽和高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点最短
路程是_____________.
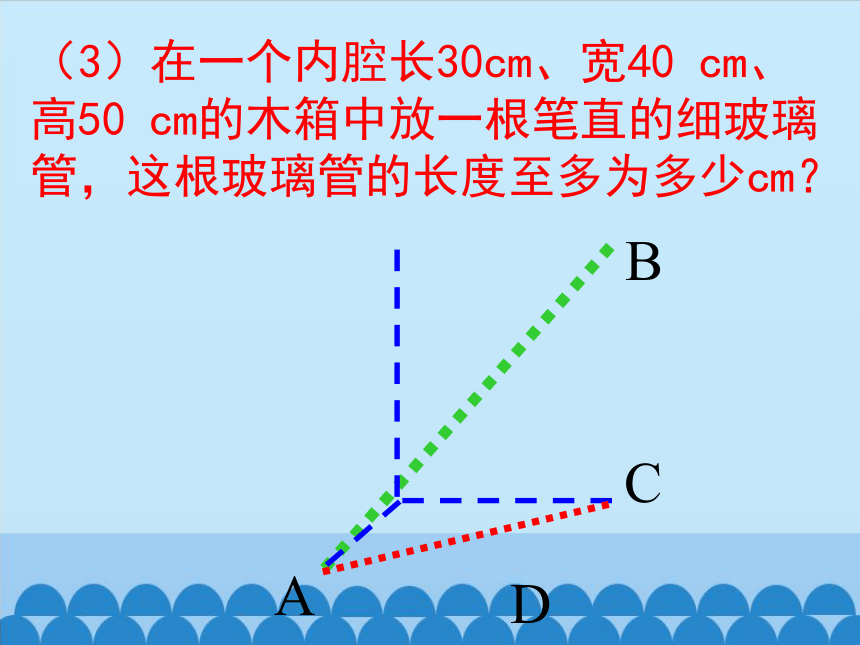
(3)在一个内腔长30cm、宽40 cm、高50 cm的木箱中放一根笔直的细玻璃管,这根玻璃管的长度至多为多少cm?
A
C
B
D
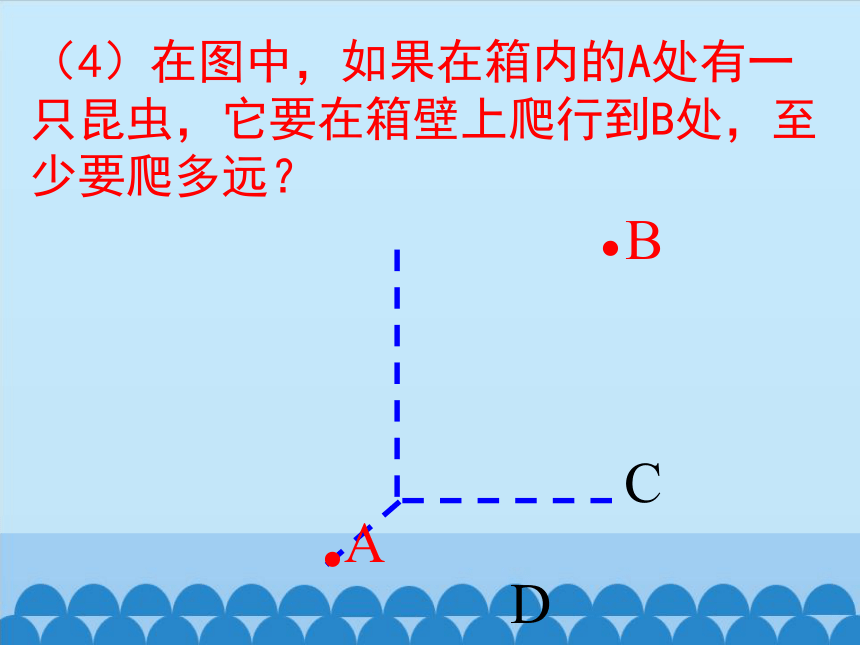
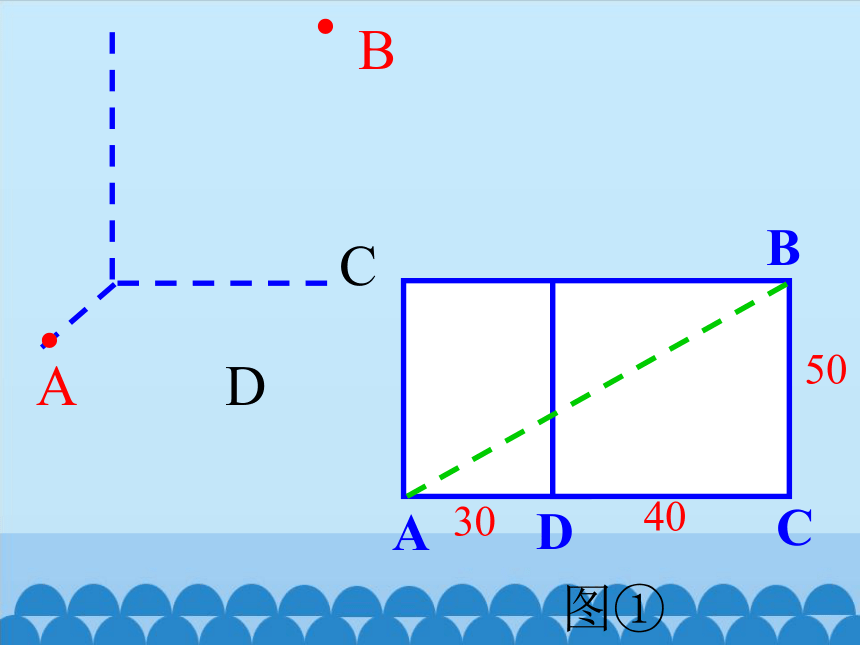
(4)在图中,如果在箱内的A处有一只昆虫,它要在箱壁上爬行到B处,至少要爬多远?
C
D
A
.
B
.
图①
A
C
B
D
30
40
50
C
D
A
.
B
.
图②
A
C
B
D
30
50
40
C
D
A
.
B
.
C
C
D
A
.
B
.
A
C
B
D
图③
30
40
50
例2.如图,A,B是直线l外同侧的两点,且点A和点B到l的距离分别是3㎝和5㎝,AB=12㎝,若点P在l上移动,求PA+PB的最小值。
· A
· B
l
例3.有一个如图所示的长方体的透明玻璃鱼缸,假设其长AD=80cm,高AB=60cm,水深为AE=40cm,在水面上紧贴内壁G处有一鱼饵,G在水面线EF上,且EG=60cm,一小虫想从鱼缸外的A点沿壁爬进鱼缸内G处吃鱼饵.
(1)动物应该走怎样的路线才使爬的路线最短呢?请在图中画出它爬行的路线,并用箭头标注.
(2)求小动物爬行的最短路线长.
本节课你学到了什么?
谢谢!
勾股定理的应用(三)
例1. 蚂议最短路程问题.
(1) 如图所示。有一个圆柱,它的高等于12厘米,底面半径等于3厘米。在圆柱下底面的A点有一只蚂蚁,它想吃到上底面的A点相对的B点处的事物,沿着圆柱侧面需要爬行的最短路程是多少?
(п的值取3)
(2)如图是一个三级台阶,它的每一级的长宽和高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点最短
路程是_____________.
(3)在一个内腔长30cm、宽40 cm、高50 cm的木箱中放一根笔直的细玻璃管,这根玻璃管的长度至多为多少cm?
A
C
B
D
(4)在图中,如果在箱内的A处有一只昆虫,它要在箱壁上爬行到B处,至少要爬多远?
C
D
A
.
B
.
图①
A
C
B
D
30
40
50
C
D
A
.
B
.
图②
A
C
B
D
30
50
40
C
D
A
.
B
.
C
C
D
A
.
B
.
A
C
B
D
图③
30
40
50
例2.如图,A,B是直线l外同侧的两点,且点A和点B到l的距离分别是3㎝和5㎝,AB=12㎝,若点P在l上移动,求PA+PB的最小值。
· A
· B
l
例3.有一个如图所示的长方体的透明玻璃鱼缸,假设其长AD=80cm,高AB=60cm,水深为AE=40cm,在水面上紧贴内壁G处有一鱼饵,G在水面线EF上,且EG=60cm,一小虫想从鱼缸外的A点沿壁爬进鱼缸内G处吃鱼饵.
(1)动物应该走怎样的路线才使爬的路线最短呢?请在图中画出它爬行的路线,并用箭头标注.
(2)求小动物爬行的最短路线长.
本节课你学到了什么?
谢谢!
