2021年华东师大版数学八年级上册 13.3.1 等腰三角形的性质课件(20张)
文档属性
| 名称 | 2021年华东师大版数学八年级上册 13.3.1 等腰三角形的性质课件(20张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 255.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
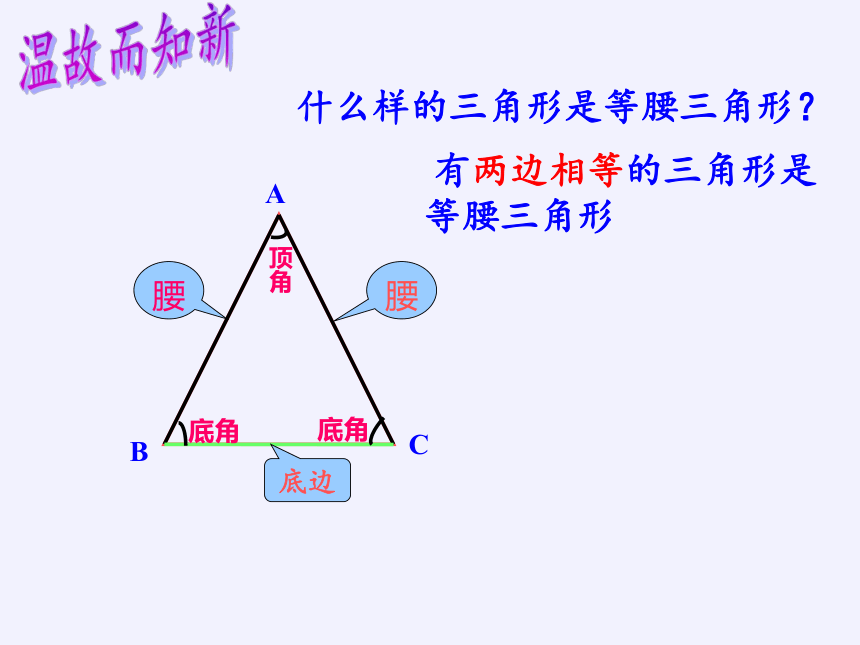
等腰三角形的性质
A
C
B
腰
腰
底边
顶角
底角
底角
有两边相等的三角形是等腰三角形
温故而知新
什么样的三角形是等腰三角形?
学习目标:
1.探索并掌握等腰三角形的两个性质.
2.会运用等腰三角形的概念和性质解决有关问题。
自学指导:
5分钟时间认真看课本75页---77页练习上面
1、思考“探究”中的问题,理解等腰三角形的定义和性质并会证明。
2、例1是如何运用等腰三角形性质并注意解题格式和步骤。
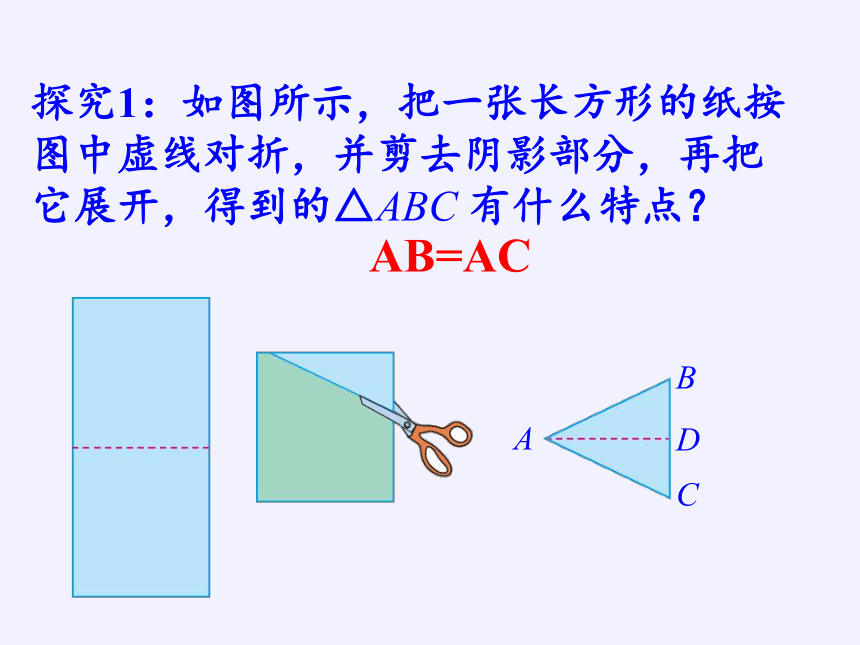
探究1:如图所示,把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC 有什么特点?
A
B
C
D
AB=AC
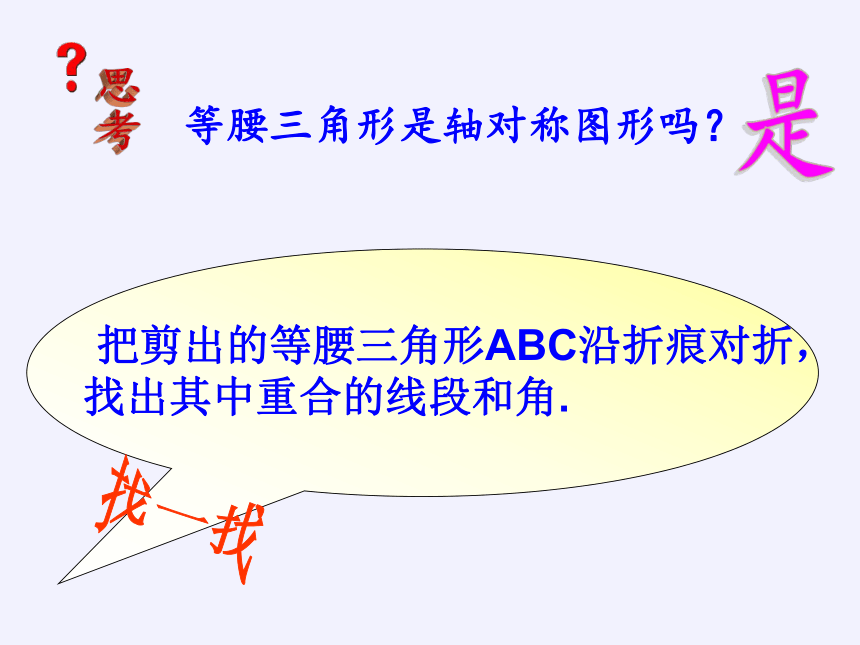
把剪出的等腰三角形ABC沿折痕对折, 找出其中重合的线段和角.
找一找
等腰三角形是轴对称图形吗?
思考
是
重合的线段 重合的角
A
C
B
D
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠BAD = ∠CAD
∠ADB = ∠ADC
等腰三角形除了两腰相等以外,
你还能发现它的其他性质吗
大胆猜想
已知:△ABC中,AB=AC
求证:∠B= C
分析:1.如何证明两个角相等?
2.如何构造两个全等的三角形?
A
B
C
D
等腰三角形的两个底角相等
猜想与论证
想一想:
由刚才证明的△ABD≌ △ACD,除了能得到∠B=∠C 你还能发现什么
重合的线段 重合的角
A
B
D
C
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠BAD = ∠CAD
∠ADB =∠ADC
=90°
等腰三角形的性质
性质 1 等腰三角形的两个底角相等
(简写成等边对等角)
性质 2 等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合 (简写成三线合一)
A
B
C
D
性质 1 在△ABC中, ∵ AB=AC
∴ ________= ________
性质 2 ( 1 ) ∵ AB=AC,AD是角平分线,
∴______⊥______,________=________ ;
( 2 ) ∵ AB=AC ,AD是中线,
∴ ⊥ ,∠ = ∠____;
( 3 ) ∵ AB=AC ,AD⊥BC,
∴∠_____=∠______,_____=______
几何语言:
A
B
C
D
∠B
∠C
AD
BC
BD
CD
AD
BC
BAD
CAD
BAD
CAD
BD
CD
⒈等腰三角形一个底角为75°,它的另外两个角为_____ __;
⒉等腰三角形一个角为70°,它的另外两个角为___________________;
75°, 30°
70°,40°或55°,55°
尝试运用
A
B
C
D
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,∠A=∠ABD
(等边对等角)
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,
从而∠ABC= ∠C= ∠BDC=2x,
于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180°,
解得x=36°,
在△ABC中,∠A=36°,∠ABC=∠C=72°
x
⌒
2x
⌒
2x
⌒
⌒
2x
例题:如图,在△ABC中 ,AB=AC,点D在AC 上,且BD=BC=AD. 求△ABC各内角的度数?
如图,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数
解:∵AB=AD=DC
∴ ∠B= ∠ADB,∠C= ∠DAC
设 ∠C=x,则 ∠DAC=x,
∠B= ∠ADB= ∠C+ ∠DAC=2x
在△ABC中,
∠B+ ∠C+ ∠BAD+ ∠DAC
=2x+x+26°+x=180°
解得:x=38.5°,
∴ ∠B=77°, ∠C= 38.5°
自学检测
轴对称图形
两个底角相等,简称“等边对等角”
顶角平分线、底边上的中线、和底边上的高互相重合,简称“三线合一”
等腰三角形
小 结
2. 能根据等腰三角形的概念与性质求等腰三角形的周长或知道一角求其它两角或证线段、角相等。
作业
必做 : 习题13.3 第1、4题
选做: 习题13.3 第6题
谢 谢
等腰三角形的性质
A
C
B
腰
腰
底边
顶角
底角
底角
有两边相等的三角形是等腰三角形
温故而知新
什么样的三角形是等腰三角形?
学习目标:
1.探索并掌握等腰三角形的两个性质.
2.会运用等腰三角形的概念和性质解决有关问题。
自学指导:
5分钟时间认真看课本75页---77页练习上面
1、思考“探究”中的问题,理解等腰三角形的定义和性质并会证明。
2、例1是如何运用等腰三角形性质并注意解题格式和步骤。
探究1:如图所示,把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC 有什么特点?
A
B
C
D
AB=AC
把剪出的等腰三角形ABC沿折痕对折, 找出其中重合的线段和角.
找一找
等腰三角形是轴对称图形吗?
思考
是
重合的线段 重合的角
A
C
B
D
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠BAD = ∠CAD
∠ADB = ∠ADC
等腰三角形除了两腰相等以外,
你还能发现它的其他性质吗
大胆猜想
已知:△ABC中,AB=AC
求证:∠B= C
分析:1.如何证明两个角相等?
2.如何构造两个全等的三角形?
A
B
C
D
等腰三角形的两个底角相等
猜想与论证
想一想:
由刚才证明的△ABD≌ △ACD,除了能得到∠B=∠C 你还能发现什么
重合的线段 重合的角
A
B
D
C
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠BAD = ∠CAD
∠ADB =∠ADC
=90°
等腰三角形的性质
性质 1 等腰三角形的两个底角相等
(简写成等边对等角)
性质 2 等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合 (简写成三线合一)
A
B
C
D
性质 1 在△ABC中, ∵ AB=AC
∴ ________= ________
性质 2 ( 1 ) ∵ AB=AC,AD是角平分线,
∴______⊥______,________=________ ;
( 2 ) ∵ AB=AC ,AD是中线,
∴ ⊥ ,∠ = ∠____;
( 3 ) ∵ AB=AC ,AD⊥BC,
∴∠_____=∠______,_____=______
几何语言:
A
B
C
D
∠B
∠C
AD
BC
BD
CD
AD
BC
BAD
CAD
BAD
CAD
BD
CD
⒈等腰三角形一个底角为75°,它的另外两个角为_____ __;
⒉等腰三角形一个角为70°,它的另外两个角为___________________;
75°, 30°
70°,40°或55°,55°
尝试运用
A
B
C
D
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,∠A=∠ABD
(等边对等角)
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,
从而∠ABC= ∠C= ∠BDC=2x,
于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180°,
解得x=36°,
在△ABC中,∠A=36°,∠ABC=∠C=72°
x
⌒
2x
⌒
2x
⌒
⌒
2x
例题:如图,在△ABC中 ,AB=AC,点D在AC 上,且BD=BC=AD. 求△ABC各内角的度数?
如图,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数
解:∵AB=AD=DC
∴ ∠B= ∠ADB,∠C= ∠DAC
设 ∠C=x,则 ∠DAC=x,
∠B= ∠ADB= ∠C+ ∠DAC=2x
在△ABC中,
∠B+ ∠C+ ∠BAD+ ∠DAC
=2x+x+26°+x=180°
解得:x=38.5°,
∴ ∠B=77°, ∠C= 38.5°
自学检测
轴对称图形
两个底角相等,简称“等边对等角”
顶角平分线、底边上的中线、和底边上的高互相重合,简称“三线合一”
等腰三角形
小 结
2. 能根据等腰三角形的概念与性质求等腰三角形的周长或知道一角求其它两角或证线段、角相等。
作业
必做 : 习题13.3 第1、4题
选做: 习题13.3 第6题
谢 谢
