华东师大版数学八年级上册 13.2.1 全等三角形 课件(共14张PPT)
文档属性
| 名称 | 华东师大版数学八年级上册 13.2.1 全等三角形 课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 00:00:00 | ||
图片预览




文档简介
(共14张PPT)
全等三角形
学习目标
1、进一步理解和掌握全等三角形的判定
3、会用判定和性质解决简单的数学问题
2、探索全等三角形的性质
全等三角形的判定
两边一角 两角一边 三边 三角 直角三角形
S.A.S S.S.A A.S.A A.A.S S.S.S A.A.A H.L
全等 不一定 全等 全等 全等 不一定 全等
复习回顾
全等判定我知道(S.A.S.) (A.S.A.) (A.A.S.) (S.S.S.)
A
B
C
D
E
F
基本性质:对应边相等,对应角相等
A
B
C
性质探究
1、已知:如图,△ABC≌△A'B'C',AD⊥BC,A'D'⊥B'C'
试猜想AD与A'D'的关系,并说明理由。
A
B
C
D
A'
c'
B'
D'
结论:全等三角形对应边上的高相等
A
B
C
D
A'
c'
B'
D'
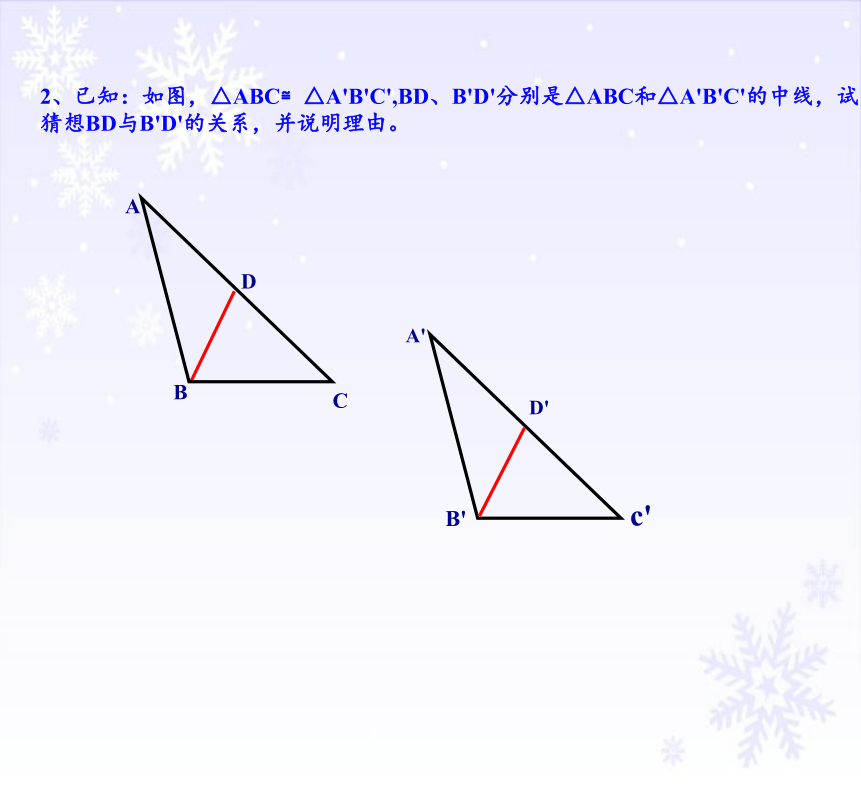
2、已知:如图,△ABC≌△A'B'C',BD、B'D'分别是△ABC和△A'B'C'的中线,试猜想BD与B'D'的关系,并说明理由。
A
B
C
D
A'
c'
B'
D'
1
2
3
4
3、已知:如图,△ABC≌△A'B'C',BD、B'D'分别是△ABC和△A'B'C'的角平分线,试猜想BD与B'D'的关系,并说明理由。
全等三角形的性质
基本性质:对应边相等,对应角相等
其它性质:全等三角形对应边上的高相等
全等三角形对应边上的中线相等
全等三角形对应边上的角平分线相等
全等三角形的周长相等、面积相等
2.如图2,△ABC≌△BAD,A和B,C和D是对应顶点,如果AB=8cm,BD=6cm,AD=5cm,则BC=___cm,△ABC的周长=__
1.如图1,把△ABD沿BD翻折到△CBD的位置,使A与C重合,则△ABD______△CBD,其对应角为________,对应边为________。
3.如图3,若△ABC≌△EBD,且BD=4cm,∠D=60°,则∠ACE=_______°,BC=________cm。
简单应用
4、沿矩形ABCD的对角线BD翻折△ABD得△A'B'D,A'D交BC于F,如图所示,△BDF是何种三角形?请说明理由.
矩形ABCD
A
B
C
D
A'
F
畅谈收获
通过本节课的学习,我知道了......
附件
长方形沿对角线对折(465).gsp
谢 谢
全等三角形
学习目标
1、进一步理解和掌握全等三角形的判定
3、会用判定和性质解决简单的数学问题
2、探索全等三角形的性质
全等三角形的判定
两边一角 两角一边 三边 三角 直角三角形
S.A.S S.S.A A.S.A A.A.S S.S.S A.A.A H.L
全等 不一定 全等 全等 全等 不一定 全等
复习回顾
全等判定我知道(S.A.S.) (A.S.A.) (A.A.S.) (S.S.S.)
A
B
C
D
E
F
基本性质:对应边相等,对应角相等
A
B
C
性质探究
1、已知:如图,△ABC≌△A'B'C',AD⊥BC,A'D'⊥B'C'
试猜想AD与A'D'的关系,并说明理由。
A
B
C
D
A'
c'
B'
D'
结论:全等三角形对应边上的高相等
A
B
C
D
A'
c'
B'
D'
2、已知:如图,△ABC≌△A'B'C',BD、B'D'分别是△ABC和△A'B'C'的中线,试猜想BD与B'D'的关系,并说明理由。
A
B
C
D
A'
c'
B'
D'
1
2
3
4
3、已知:如图,△ABC≌△A'B'C',BD、B'D'分别是△ABC和△A'B'C'的角平分线,试猜想BD与B'D'的关系,并说明理由。
全等三角形的性质
基本性质:对应边相等,对应角相等
其它性质:全等三角形对应边上的高相等
全等三角形对应边上的中线相等
全等三角形对应边上的角平分线相等
全等三角形的周长相等、面积相等
2.如图2,△ABC≌△BAD,A和B,C和D是对应顶点,如果AB=8cm,BD=6cm,AD=5cm,则BC=___cm,△ABC的周长=__
1.如图1,把△ABD沿BD翻折到△CBD的位置,使A与C重合,则△ABD______△CBD,其对应角为________,对应边为________。
3.如图3,若△ABC≌△EBD,且BD=4cm,∠D=60°,则∠ACE=_______°,BC=________cm。
简单应用
4、沿矩形ABCD的对角线BD翻折△ABD得△A'B'D,A'D交BC于F,如图所示,△BDF是何种三角形?请说明理由.
矩形ABCD
A
B
C
D
A'
F
畅谈收获
通过本节课的学习,我知道了......
附件
长方形沿对角线对折(465).gsp
谢 谢
