八年级上数学第十四章勾股定理单元测试(有答案)
文档属性
| 名称 | 八年级上数学第十四章勾股定理单元测试(有答案) | 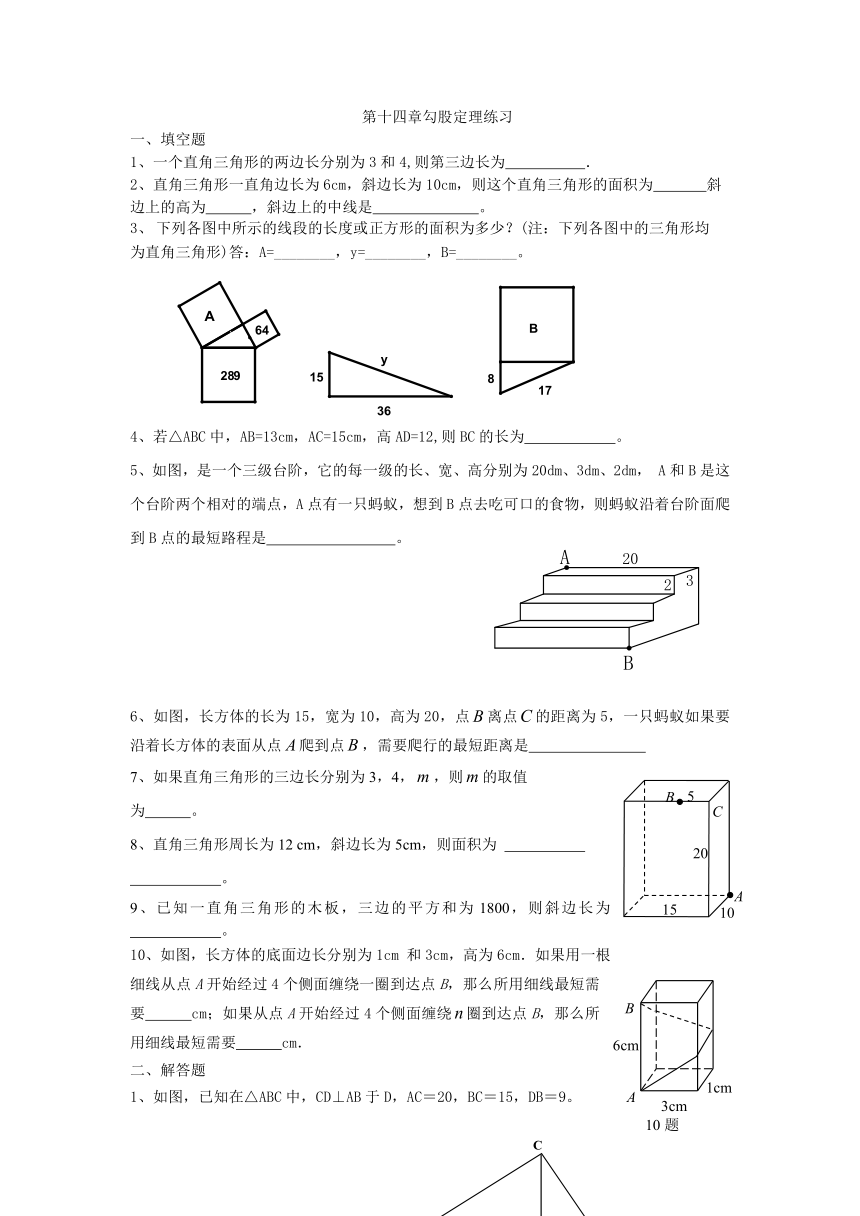 | |
| 格式 | zip | ||
| 文件大小 | 32.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-27 12:44:21 | ||
图片预览

文档简介
第十四章勾股定理练习
一、填空题
1、一个直角三角形的两边长分别为3和4,则第三边长为 .
2、直角三角形一直角边长为6cm,斜边长为10cm,则这个直角三角形的面积为 斜边上的高为 ,斜边上的中线是 。
下列各图中所示的线段的长度或正方形的面积为多少?(注:下列各图中的三角形均
为直角三角形)答:A=________,y=________,B=________。
4、若△ABC中,AB=13cm,AC=15cm,高AD=12,则BC的长为 。
5、如图,是一个三级台阶,它的每一级的长、宽、高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点的最短路程是 。
6、如图,长方体的长为15,宽为10,高为20,点离点的距离为5,一只蚂蚁如果要沿着长方体的表面从点爬到点,需要爬行的最短距离是
7、如果直角三角形的三边长分别为3,4,,则的取值
为 。
8、直角三角形周长为12 cm,斜边长为5cm,则面积为 。
9、已知一直角三角形的木板,三边的平方和为1800,则斜边长为 。
10、如图,长方体的底面边长分别为1cm 和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要 cm;如果从点A开始经过4个侧面缠绕圈到达点B,那么所用细线最短需要 cm.
二、解答题
1、如图,已知在△ABC中,CD⊥AB于D,AC=20,BC=15,DB=9。
(1)求DC的长。
(2)求AB的长。
2、如图,在海上观察所A,我边防海警发现正北6km的B处有一可疑船只正在向东方向8km的C处行驶.我边防海警即刻派船前往C处拦截.若可疑船只的行驶速度为40km/h,则我边防海警船的速度为多少时,才能恰好在C处将可疑船只截住?
3、已知:如图,△ABC中,AB=3,BC=4,∠B=90°,若将△ABC折叠,使C点与A点重合,求折痕EF的长。(提示:设FC=x)
4、如图,设四边形ABCD是边长为1的正方形,以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以第二个正方形的对角线AE为边作第三个正方形AEGH,如此下去…。(1)记正方形ABCD的边长,依上述方法所作的正方形的边长依次为,的值。(2)根据以上规律写出第n个正方形的边长的表达式。
答案
一、
1、5或; 2、24,4?8,5 ; 3、225, ,225;4、14或4;
5、25dm ;6、25;7、或5 ;8、6cm2;9、30; 10、10,;
二、
1、DC=12 、AB=25 2、50km/h 3、2?5 4、,,
一、填空题
1、一个直角三角形的两边长分别为3和4,则第三边长为 .
2、直角三角形一直角边长为6cm,斜边长为10cm,则这个直角三角形的面积为 斜边上的高为 ,斜边上的中线是 。
下列各图中所示的线段的长度或正方形的面积为多少?(注:下列各图中的三角形均
为直角三角形)答:A=________,y=________,B=________。
4、若△ABC中,AB=13cm,AC=15cm,高AD=12,则BC的长为 。
5、如图,是一个三级台阶,它的每一级的长、宽、高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点的最短路程是 。
6、如图,长方体的长为15,宽为10,高为20,点离点的距离为5,一只蚂蚁如果要沿着长方体的表面从点爬到点,需要爬行的最短距离是
7、如果直角三角形的三边长分别为3,4,,则的取值
为 。
8、直角三角形周长为12 cm,斜边长为5cm,则面积为 。
9、已知一直角三角形的木板,三边的平方和为1800,则斜边长为 。
10、如图,长方体的底面边长分别为1cm 和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要 cm;如果从点A开始经过4个侧面缠绕圈到达点B,那么所用细线最短需要 cm.
二、解答题
1、如图,已知在△ABC中,CD⊥AB于D,AC=20,BC=15,DB=9。
(1)求DC的长。
(2)求AB的长。
2、如图,在海上观察所A,我边防海警发现正北6km的B处有一可疑船只正在向东方向8km的C处行驶.我边防海警即刻派船前往C处拦截.若可疑船只的行驶速度为40km/h,则我边防海警船的速度为多少时,才能恰好在C处将可疑船只截住?
3、已知:如图,△ABC中,AB=3,BC=4,∠B=90°,若将△ABC折叠,使C点与A点重合,求折痕EF的长。(提示:设FC=x)
4、如图,设四边形ABCD是边长为1的正方形,以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以第二个正方形的对角线AE为边作第三个正方形AEGH,如此下去…。(1)记正方形ABCD的边长,依上述方法所作的正方形的边长依次为,的值。(2)根据以上规律写出第n个正方形的边长的表达式。
答案
一、
1、5或; 2、24,4?8,5 ; 3、225, ,225;4、14或4;
5、25dm ;6、25;7、或5 ;8、6cm2;9、30; 10、10,;
二、
1、DC=12 、AB=25 2、50km/h 3、2?5 4、,,
