人教版七年级上册数学第一章有理数课件 1.2.1有理数(23张ppt)
文档属性
| 名称 | 人教版七年级上册数学第一章有理数课件 1.2.1有理数(23张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 325.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 09:55:25 | ||
图片预览






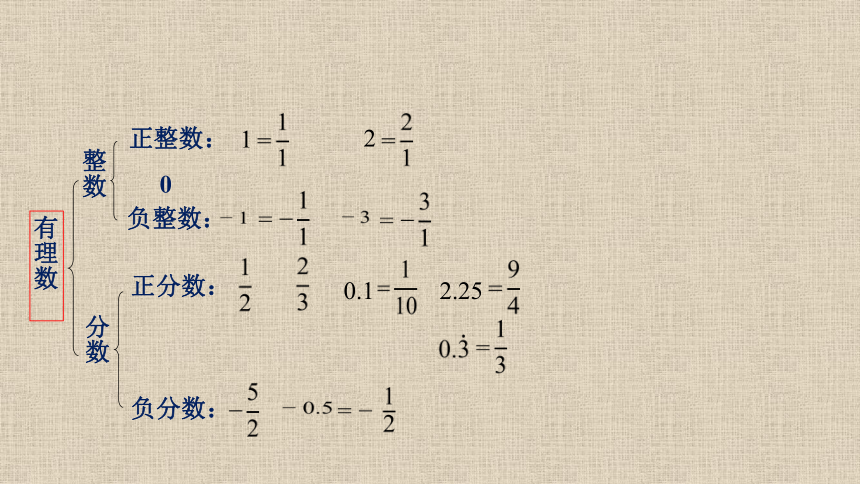


文档简介
(共23张PPT)
有理数
1.通过上节课的学习,你知道除了正数外
还有什么数?
还包括0和负数
0 既不是正数,也不是负数
复习回顾
用正数和负数表示具有相反意义的量
-2m
0m
那么这个物体向左移动2m,记作移动
原地不动,记作移动
例如:一个物体向右移动3m,记作移动+3m,
复习回顾
1 , , 1 , 0.5 , 2 , 3 , 0 , , 0.1 , 0. , , 2.25
以上各数中,哪些是小学学过的数
哪些是中学学过的数
你能试着将它们分类吗
想一想
1 , , 1 , 0.5 , 2 , 3 , 0 , , 0.1 , 0. , , 2.25
复习回顾
小学学过的数:
中学学过的数:
, 1 , 2 , 0 , , 0.1 , 0. , 2.25
1 , 0.5 , 3 ,
正整数:
0
正分数:
负整数:
负分数:
分数
整数
1
2
1
3
正整数:
0
正分数:
负整数:
负分数:
分数
整数
有理数
1
2
1
0.1
2.25
0.5
3
(1)正整数 、0 、负整数 统称为整数;
正分数 、 负分数 统称为分数.
(2) 整数和分数 统称为有理数.
明朝科学家 徐光启
形成概念
你能试着对有理数进行分类吗?
试一试
方法1.按定义分类:
有理数
整数
分数
正整数
负整数
0
正分数
负分数
形成概念
方法2.按符号分类:
有理数
正有理数
负有理数
正整数
正分数
0
负整数
负分数
形成概念
按符号分类:
有
理
数
正有理数
负有理数
正整数
正分数
0
负整数
负分数
有
理
数
整数
分数
正整数
负整数
0
正分数
负分数
按定义分类:
0既不是正数也不是负数,
分类时要格外注意
说明:
正数 负数 整数 分数 有理数
15
+6
0
2018
0.9
例1判断
表中各数分别是什么数,在相应的空格中划√
典例精析
例2. 所有正数组成正数集合,所有负数组成负数集合.把下面的有理数填入它属于的集合的圈内:
正数集合
负数集合
18 , , 5 , , , 95% , 4.95 , 80, 123 , 3.14
典例精析
正数集合
负数集合
18 , , 5 , , , 95% , 4.95 , 80, 123 , 3.14
18
95%
3.14
123
4.95
80
5
典例精析
例2. 所有正数组成正数集合,所有负数组成负数集合.把下面的有理数填入它属于的集合的圈内:
正数集合
负数集合
18
95%
3.14
123
4.95
80
5
0既不在正数集合中,也不在负数集合中!
如果这里有0这个数字,它应该分在哪个集合里?
想一想:
①零是整数;
②零是有理数;
③零是自然数;
④零是正数;
⑤零是负数;
⑥零是非负数.
例3.下列说法中,其中正确的是
典例精析
①零是整数;
②零是有理数;
③零是自然数;
④零是正数;
⑤零是负数;
⑥零是非负数.
例3.下列说法中,其中正确的是
√
√
√
×
×
√
① ② ③ ⑥
非负数:
0和正数
典例精析
如果将非负数改为非负整数,
那么它指的是哪些数呢?
想一想:
非负整数:
0和正整数
非正数:
非负数:
0和负数
自然数
非正整数:
0和负整数
0和正数
整数、分数 统称为有理数.
课堂小结
1 有理数的概念:
课堂小结
2 有理数的分类:
有理数
整数
分数
正整数
负整数
0
正分数
负分数
按定义分类:
课堂小结
2 有理数的分类:
有理数
按符号分类:
正有理数
负有理数
正整数
正分数
0
负整数
负分数
有理数分类时,
注意分类标准,
做到不重不漏.
注意
有理数
1.通过上节课的学习,你知道除了正数外
还有什么数?
还包括0和负数
0 既不是正数,也不是负数
复习回顾
用正数和负数表示具有相反意义的量
-2m
0m
那么这个物体向左移动2m,记作移动
原地不动,记作移动
例如:一个物体向右移动3m,记作移动+3m,
复习回顾
1 , , 1 , 0.5 , 2 , 3 , 0 , , 0.1 , 0. , , 2.25
以上各数中,哪些是小学学过的数
哪些是中学学过的数
你能试着将它们分类吗
想一想
1 , , 1 , 0.5 , 2 , 3 , 0 , , 0.1 , 0. , , 2.25
复习回顾
小学学过的数:
中学学过的数:
, 1 , 2 , 0 , , 0.1 , 0. , 2.25
1 , 0.5 , 3 ,
正整数:
0
正分数:
负整数:
负分数:
分数
整数
1
2
1
3
正整数:
0
正分数:
负整数:
负分数:
分数
整数
有理数
1
2
1
0.1
2.25
0.5
3
(1)正整数 、0 、负整数 统称为整数;
正分数 、 负分数 统称为分数.
(2) 整数和分数 统称为有理数.
明朝科学家 徐光启
形成概念
你能试着对有理数进行分类吗?
试一试
方法1.按定义分类:
有理数
整数
分数
正整数
负整数
0
正分数
负分数
形成概念
方法2.按符号分类:
有理数
正有理数
负有理数
正整数
正分数
0
负整数
负分数
形成概念
按符号分类:
有
理
数
正有理数
负有理数
正整数
正分数
0
负整数
负分数
有
理
数
整数
分数
正整数
负整数
0
正分数
负分数
按定义分类:
0既不是正数也不是负数,
分类时要格外注意
说明:
正数 负数 整数 分数 有理数
15
+6
0
2018
0.9
例1判断
表中各数分别是什么数,在相应的空格中划√
典例精析
例2. 所有正数组成正数集合,所有负数组成负数集合.把下面的有理数填入它属于的集合的圈内:
正数集合
负数集合
18 , , 5 , , , 95% , 4.95 , 80, 123 , 3.14
典例精析
正数集合
负数集合
18 , , 5 , , , 95% , 4.95 , 80, 123 , 3.14
18
95%
3.14
123
4.95
80
5
典例精析
例2. 所有正数组成正数集合,所有负数组成负数集合.把下面的有理数填入它属于的集合的圈内:
正数集合
负数集合
18
95%
3.14
123
4.95
80
5
0既不在正数集合中,也不在负数集合中!
如果这里有0这个数字,它应该分在哪个集合里?
想一想:
①零是整数;
②零是有理数;
③零是自然数;
④零是正数;
⑤零是负数;
⑥零是非负数.
例3.下列说法中,其中正确的是
典例精析
①零是整数;
②零是有理数;
③零是自然数;
④零是正数;
⑤零是负数;
⑥零是非负数.
例3.下列说法中,其中正确的是
√
√
√
×
×
√
① ② ③ ⑥
非负数:
0和正数
典例精析
如果将非负数改为非负整数,
那么它指的是哪些数呢?
想一想:
非负整数:
0和正整数
非正数:
非负数:
0和负数
自然数
非正整数:
0和负整数
0和正数
整数、分数 统称为有理数.
课堂小结
1 有理数的概念:
课堂小结
2 有理数的分类:
有理数
整数
分数
正整数
负整数
0
正分数
负分数
按定义分类:
课堂小结
2 有理数的分类:
有理数
按符号分类:
正有理数
负有理数
正整数
正分数
0
负整数
负分数
有理数分类时,
注意分类标准,
做到不重不漏.
注意
