人教版七年级上册数学第二章整式的加减课件-整式的加减(五)(33张ppt)
文档属性
| 名称 | 人教版七年级上册数学第二章整式的加减课件-整式的加减(五)(33张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 673.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 10:09:38 | ||
图片预览









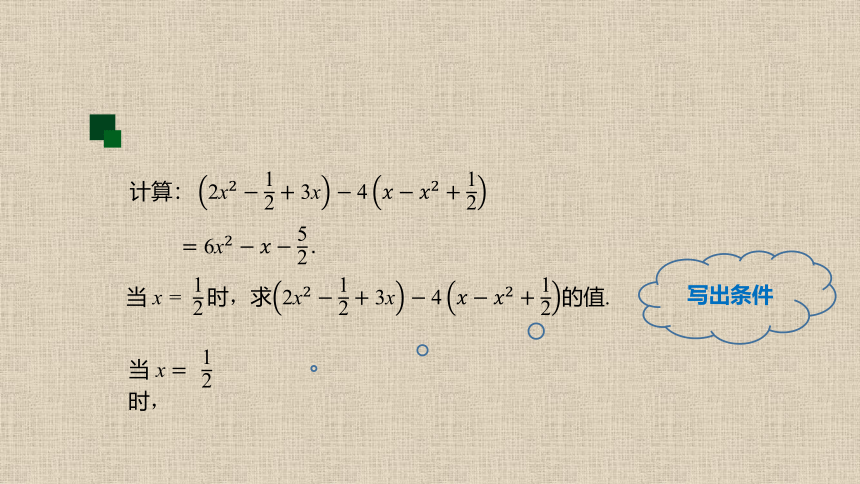
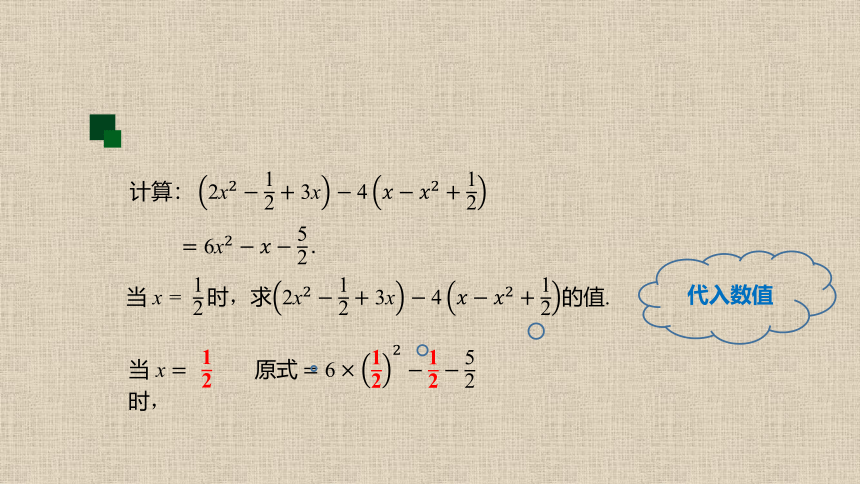
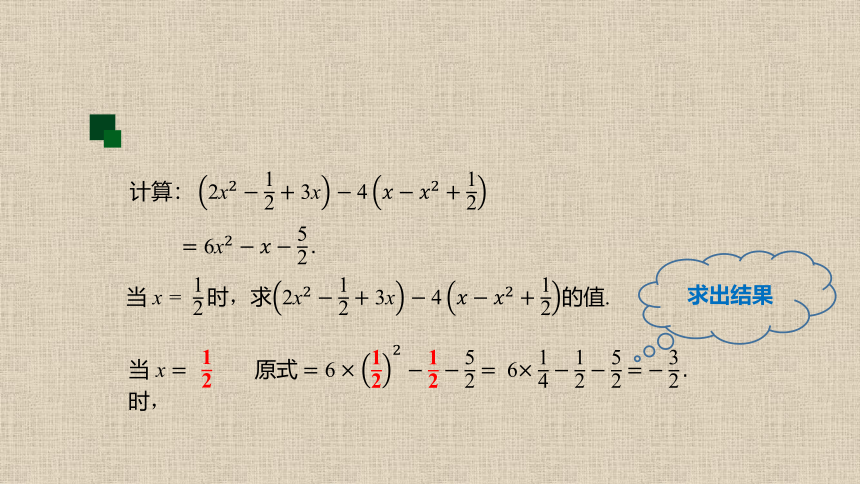
文档简介
(共33张PPT)
整式的加减(五)
一、知识回顾
整式加减的运算法则:
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.
整式加减的运算法则:
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.
整式加减的运算法则:
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.
整式加减的运算法则:
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.
整式加减的运算法则:
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.
整式加减的运算法则:
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.
去括号
整式加减的运算法则:
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.
去括号
合并同类项
当 x = ,求的值.
二、学习新知
当 x = ,求的值.
当 x 时,
写出条件
当 x = ,求的值.
当 x 时,
原式
代入数值
当 x = ,求的值.
当 x 时,
原式 6
求出结果
当x时,
原式 6
先化简,
再求值,
可以简化计算
当 x = ,求的值.
当 x 时,
原式 6
当 x = ,求的值.
书写格式
去括号
合并同类项
写出条件
代入、求值
例1.求 的值,其中x= 2,y
三、典型例题
例1.求 的值,其中x= 2,y
解:
例1.求 的值,其中x= 2,y
解:
=
例1.求 的值,其中x= 2,y
解:
=
例1.求 的值,其中x= 2,y
解:
=
= 3x+.
例1.求 的值,其中x= 2,y
解:
=
= 3x+.
先化简
例1.求 的值,其中x= 2,y
解:
=
= 3x+.
先化简
当 x = 2,y 时,
例1.求 的值,其中x= 2,y
解:
=
= 3x+.
先化简
当 x = 2,y 时,
原式= = .
例1.求 的值,其中x= 2,y
解:
=
= 3x+.
先化简
当 x = 2,y 时,
原式= = .
再求值
例1.求 的值,其中x= 2,y
解:
=
= 3x+.
书写格式
当 x = 2,y 时,
原式= = .
去括号
合并同类项
写出条件
代入、求值
例2.窗户的形状如图所示(图中长度单位:cm),其上部是半圆形,下部是边长相同的四个小正方形.已知下部小正方形的边长是a cm.计算:
(1)窗户的面积;
(2)窗户的外框的总长;
(3)当a=2 cm时,
窗户的面积是多少?
四、实际应用
例2.窗户的形状如图所示(图中长度单位:cm),其上部是半圆形,下部是边长相同的四个小正方形.已知下部小正方形的边长是a cm.计算:
(1)窗户的面积;
(2)窗户的外框的总长;
(3)当a=2 cm时,
窗户的面积是多少?
例2.窗户的形状如图所示(图中长度单位:cm),其上部是半圆形,下部是边长相同的四个小正方形.已知下部小正方形的边长是a cm.计算:
(1)窗户的面积(单位:);
解:半圆的面积
四个小正方形的面积之和
窗户的面积
合并
同类项
例2.窗户的形状如图所示(图中长度单位:cm),其上部是半圆形,下部是边长相同的四个小正方形.已知下部小正方形的边长是a cm.计算:
(1)窗户的面积(单位:);
解:半圆的面积
四个小正方形的面积之和
窗户的面积
.
例2.窗户的形状如图所示(图中长度单位:cm),其上部是半圆形,下部是边长相同的四个小正方形.已知下部小正方形的边长是a cm.计算:
(2)窗户外框的总长(单位: cm );
解:窗户上部半圆的长度
窗户下部外框长度之和
窗户外框的总长
合并
同类项
例2.窗户的形状如图所示(图中长度单位:cm),其上部是半圆形,下部是边长相同的四个小正方形.已知下部小正方形的边长是a cm.计算:
(2)窗户外框的总长(单位: cm );
解:窗户上部半圆的长度
窗户下部外框长度之和
窗户外框的总长
.
例2.窗户的形状如图所示(图中长度单位:cm),其上部是半圆形,下部是边长相同的四个小正方形.已知下部小正方形的边长是a cm.计算:
(3)当a=2 cm时,窗户的面积是多少?(单位:)
解:窗户的面积
,
当a=2 cm时,
窗户的面积 =
代入求值
例2.窗户的形状如图所示(图中长度单位:cm),其上部是半圆形,下部是边长相同的四个小正方形.已知下部小正方形的边长是a cm.计算:
(3)当a=2 cm时,窗户的面积是多少?(单位:)
解:窗户的面积
,
当a=2 cm时,
窗户的面积 = .
求出结果
2 . 化简求值的过程中,类比,数式通性.
(2)化简求值的书写格式:
去括号;合并同类项;写出条件;代入数值;求出结果.
1.(1)化简求值的基本思路:先化简,再求值.
五、课堂小结
整式的加减(五)
一、知识回顾
整式加减的运算法则:
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.
整式加减的运算法则:
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.
整式加减的运算法则:
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.
整式加减的运算法则:
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.
整式加减的运算法则:
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.
整式加减的运算法则:
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.
去括号
整式加减的运算法则:
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.
去括号
合并同类项
当 x = ,求的值.
二、学习新知
当 x = ,求的值.
当 x 时,
写出条件
当 x = ,求的值.
当 x 时,
原式
代入数值
当 x = ,求的值.
当 x 时,
原式 6
求出结果
当x时,
原式 6
先化简,
再求值,
可以简化计算
当 x = ,求的值.
当 x 时,
原式 6
当 x = ,求的值.
书写格式
去括号
合并同类项
写出条件
代入、求值
例1.求 的值,其中x= 2,y
三、典型例题
例1.求 的值,其中x= 2,y
解:
例1.求 的值,其中x= 2,y
解:
=
例1.求 的值,其中x= 2,y
解:
=
例1.求 的值,其中x= 2,y
解:
=
= 3x+.
例1.求 的值,其中x= 2,y
解:
=
= 3x+.
先化简
例1.求 的值,其中x= 2,y
解:
=
= 3x+.
先化简
当 x = 2,y 时,
例1.求 的值,其中x= 2,y
解:
=
= 3x+.
先化简
当 x = 2,y 时,
原式= = .
例1.求 的值,其中x= 2,y
解:
=
= 3x+.
先化简
当 x = 2,y 时,
原式= = .
再求值
例1.求 的值,其中x= 2,y
解:
=
= 3x+.
书写格式
当 x = 2,y 时,
原式= = .
去括号
合并同类项
写出条件
代入、求值
例2.窗户的形状如图所示(图中长度单位:cm),其上部是半圆形,下部是边长相同的四个小正方形.已知下部小正方形的边长是a cm.计算:
(1)窗户的面积;
(2)窗户的外框的总长;
(3)当a=2 cm时,
窗户的面积是多少?
四、实际应用
例2.窗户的形状如图所示(图中长度单位:cm),其上部是半圆形,下部是边长相同的四个小正方形.已知下部小正方形的边长是a cm.计算:
(1)窗户的面积;
(2)窗户的外框的总长;
(3)当a=2 cm时,
窗户的面积是多少?
例2.窗户的形状如图所示(图中长度单位:cm),其上部是半圆形,下部是边长相同的四个小正方形.已知下部小正方形的边长是a cm.计算:
(1)窗户的面积(单位:);
解:半圆的面积
四个小正方形的面积之和
窗户的面积
合并
同类项
例2.窗户的形状如图所示(图中长度单位:cm),其上部是半圆形,下部是边长相同的四个小正方形.已知下部小正方形的边长是a cm.计算:
(1)窗户的面积(单位:);
解:半圆的面积
四个小正方形的面积之和
窗户的面积
.
例2.窗户的形状如图所示(图中长度单位:cm),其上部是半圆形,下部是边长相同的四个小正方形.已知下部小正方形的边长是a cm.计算:
(2)窗户外框的总长(单位: cm );
解:窗户上部半圆的长度
窗户下部外框长度之和
窗户外框的总长
合并
同类项
例2.窗户的形状如图所示(图中长度单位:cm),其上部是半圆形,下部是边长相同的四个小正方形.已知下部小正方形的边长是a cm.计算:
(2)窗户外框的总长(单位: cm );
解:窗户上部半圆的长度
窗户下部外框长度之和
窗户外框的总长
.
例2.窗户的形状如图所示(图中长度单位:cm),其上部是半圆形,下部是边长相同的四个小正方形.已知下部小正方形的边长是a cm.计算:
(3)当a=2 cm时,窗户的面积是多少?(单位:)
解:窗户的面积
,
当a=2 cm时,
窗户的面积 =
代入求值
例2.窗户的形状如图所示(图中长度单位:cm),其上部是半圆形,下部是边长相同的四个小正方形.已知下部小正方形的边长是a cm.计算:
(3)当a=2 cm时,窗户的面积是多少?(单位:)
解:窗户的面积
,
当a=2 cm时,
窗户的面积 = .
求出结果
2 . 化简求值的过程中,类比,数式通性.
(2)化简求值的书写格式:
去括号;合并同类项;写出条件;代入数值;求出结果.
1.(1)化简求值的基本思路:先化简,再求值.
五、课堂小结
