人教版七年级上册数学第二章整式的加减课件-小结复习(二)(24张ppt)
文档属性
| 名称 | 人教版七年级上册数学第二章整式的加减课件-小结复习(二)(24张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 332.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
小结复习(二)
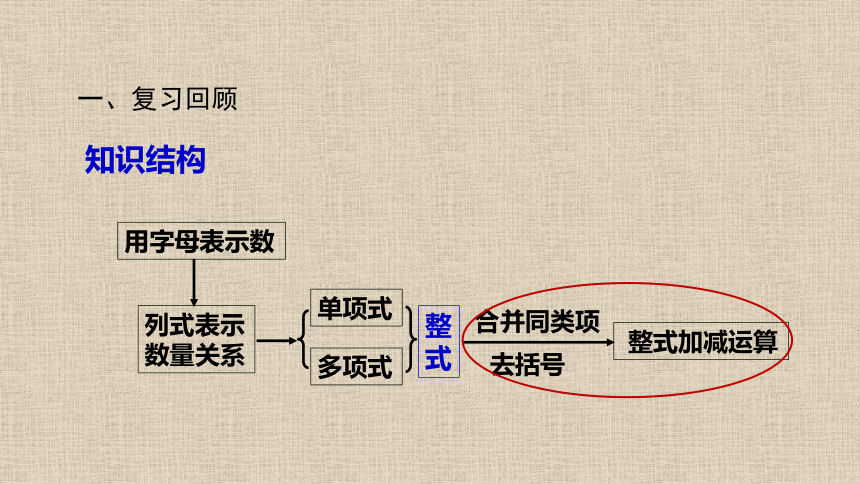
用字母表示数
列式表示数量关系
单项式
多项式
整式
整式加减运算
合并同类项
去括号
知识结构
一、复习回顾
1. 去括号
括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;
(1) 法则:
(2) 依据
乘法分配律
一、复习回顾
括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
练一练
2x –2
– 2x +2
– x2 –2 x+1
注意:不要漏乘,也不要弄错各项的符号.
1. 去括号:
;
.
;
(1)
(2)
(3)
2. 同类项
定义 所含字母相同,并且相同字母的指数也相同的项叫做同类项. 几个常数项也是同类项.
一、复习回顾
若 与 是同类项,则 x = ___,y = ___.
例如, 与 是同类项,
与 1.9 是同类项,
与 不是同类项.
3
1
试一试
把多项式中的同类项合并成一项, 叫做合并同类项.
3. 合并同类项
(1) 定义
(2) 法则:
(3) 法则依据
乘法分配律
合并同类项后,所得项的系数是合并前各同类项系数的和, 且字母连同它的指数不变.
一、复习回顾
例如,
2. 合并下列各式的同类项:
;
.
;
– 2xy
ab3 – 1.2a3b
注意:合并同类项时,可以边找边合并,不要漏项.
(1)
(2)
(3)
练一练
4. 整式的加减
运算法则: 一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.
一、复习回顾
例1 化简:
如何正确化简?
——— 应先去括号,再合并同类项.
二、典型例题
(1)
(2)
(3)
二、典型例题
解:
(1)
例1 化简:
二、典型例题
(2)
解:
例1 化简:
二、典型例题
例1 化简:
(3)
解:
(3)
二、典型例题
例1 化简:
解:
例2 求 的值,其中
解:
当 时,
原式
注意:1. 负数(或分数)代入时要加括号;
2. 省略的乘号在求值时要“复现”.
二、典型例题
分析一:
解:
原式
例3 已知: ,求 的值.
当 时,
将 表示为 后,代入 .
二、典型例题
解:
原式
用 表示 后代入,即 .
例3 已知: ,求 的值.
分析二:
当 时,
二、典型例题
解:
原式
用含b 的式子表示 a,即 再代入.
分析三:
当 时,
例3 已知: ,求 的值.
二、典型例题
小结
用含b 的式子表示 a,即 再代入.
分析三:
用 表示 后代入,即 .
分析二:
分析一:
将 表示为 后,代入 .
二、典型例题
例3 已知: ,求 的值.
法 则
依 据
去括号
三、课堂小结
1. 整式加减的基础是去括号和合并同类项
法则及依据
合并同类项的定义
同类项的定义
合并同类项
1. 整式加减的基础是去括号和合并同类项
三、课堂小结
2. 求整式的值时,要先化简,再代入求值.
在代入求值时,常有两种方法:
直接代入和间接代入(如整体代入),
当整体代入时,要认真审题,注重对条件的分析,发现已知和未知之间的隐含关系.
三、课堂小结
思考
某同学做一道数学题,“已知两个多项式 A、B,B=2x2+3x-4,试
求 A-2B”.这位同学把“A-2B”误看成“A+2B”,结果求出的答案
为5x2+8x-10. 请你替这位同学求出“A-2B”的正确答案.
分析:
从“A-2B =?”与“A+2B”的关系入手……
A-2B =(A+2B) -4B
思考 某同学做一道数学题,“已知两个多项式A、B,B=2x2+3x-4,试求 A-2B”.这位同学把“A-2B”误看成“A+2B”,结果求出的答案为5x2+8x-10. 请你替这位同学求出“A-2B”的正确答案.
=(5x2+8x-10)-4(2x2+3x-4)
=5x2+8x-10-8x2-12x+16
=-3x2-4x+6.
分析:
由题意可知
思考 某同学做一道数学题,“已知两个多项式A、B,B=2x2+3x-4,试
求 A-2B”.这位同学把“A-2B”误看成“A+2B”,结果求出的答案
为5x2+8x-10. 请你替这位同学求出“A-2B”的正确答案.
A+2B=5x2+8x-10,
所以 A =5x2+8x-10-2B
=5x2+8x-10-2(2x2+3x-4)
=5x2+8x-10-4x2-6x+8
=x2+2x-2.
A-2B
=(x2+2x-2)-2(2x2+3x-4)
=x2+2x-2-4x2-6x+8
=-3x2-4x+6.
小结复习(二)
用字母表示数
列式表示数量关系
单项式
多项式
整式
整式加减运算
合并同类项
去括号
知识结构
一、复习回顾
1. 去括号
括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;
(1) 法则:
(2) 依据
乘法分配律
一、复习回顾
括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
练一练
2x –2
– 2x +2
– x2 –2 x+1
注意:不要漏乘,也不要弄错各项的符号.
1. 去括号:
;
.
;
(1)
(2)
(3)
2. 同类项
定义 所含字母相同,并且相同字母的指数也相同的项叫做同类项. 几个常数项也是同类项.
一、复习回顾
若 与 是同类项,则 x = ___,y = ___.
例如, 与 是同类项,
与 1.9 是同类项,
与 不是同类项.
3
1
试一试
把多项式中的同类项合并成一项, 叫做合并同类项.
3. 合并同类项
(1) 定义
(2) 法则:
(3) 法则依据
乘法分配律
合并同类项后,所得项的系数是合并前各同类项系数的和, 且字母连同它的指数不变.
一、复习回顾
例如,
2. 合并下列各式的同类项:
;
.
;
– 2xy
ab3 – 1.2a3b
注意:合并同类项时,可以边找边合并,不要漏项.
(1)
(2)
(3)
练一练
4. 整式的加减
运算法则: 一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.
一、复习回顾
例1 化简:
如何正确化简?
——— 应先去括号,再合并同类项.
二、典型例题
(1)
(2)
(3)
二、典型例题
解:
(1)
例1 化简:
二、典型例题
(2)
解:
例1 化简:
二、典型例题
例1 化简:
(3)
解:
(3)
二、典型例题
例1 化简:
解:
例2 求 的值,其中
解:
当 时,
原式
注意:1. 负数(或分数)代入时要加括号;
2. 省略的乘号在求值时要“复现”.
二、典型例题
分析一:
解:
原式
例3 已知: ,求 的值.
当 时,
将 表示为 后,代入 .
二、典型例题
解:
原式
用 表示 后代入,即 .
例3 已知: ,求 的值.
分析二:
当 时,
二、典型例题
解:
原式
用含b 的式子表示 a,即 再代入.
分析三:
当 时,
例3 已知: ,求 的值.
二、典型例题
小结
用含b 的式子表示 a,即 再代入.
分析三:
用 表示 后代入,即 .
分析二:
分析一:
将 表示为 后,代入 .
二、典型例题
例3 已知: ,求 的值.
法 则
依 据
去括号
三、课堂小结
1. 整式加减的基础是去括号和合并同类项
法则及依据
合并同类项的定义
同类项的定义
合并同类项
1. 整式加减的基础是去括号和合并同类项
三、课堂小结
2. 求整式的值时,要先化简,再代入求值.
在代入求值时,常有两种方法:
直接代入和间接代入(如整体代入),
当整体代入时,要认真审题,注重对条件的分析,发现已知和未知之间的隐含关系.
三、课堂小结
思考
某同学做一道数学题,“已知两个多项式 A、B,B=2x2+3x-4,试
求 A-2B”.这位同学把“A-2B”误看成“A+2B”,结果求出的答案
为5x2+8x-10. 请你替这位同学求出“A-2B”的正确答案.
分析:
从“A-2B =?”与“A+2B”的关系入手……
A-2B =(A+2B) -4B
思考 某同学做一道数学题,“已知两个多项式A、B,B=2x2+3x-4,试求 A-2B”.这位同学把“A-2B”误看成“A+2B”,结果求出的答案为5x2+8x-10. 请你替这位同学求出“A-2B”的正确答案.
=(5x2+8x-10)-4(2x2+3x-4)
=5x2+8x-10-8x2-12x+16
=-3x2-4x+6.
分析:
由题意可知
思考 某同学做一道数学题,“已知两个多项式A、B,B=2x2+3x-4,试
求 A-2B”.这位同学把“A-2B”误看成“A+2B”,结果求出的答案
为5x2+8x-10. 请你替这位同学求出“A-2B”的正确答案.
A+2B=5x2+8x-10,
所以 A =5x2+8x-10-2B
=5x2+8x-10-2(2x2+3x-4)
=5x2+8x-10-4x2-6x+8
=x2+2x-2.
A-2B
=(x2+2x-2)-2(2x2+3x-4)
=x2+2x-2-4x2-6x+8
=-3x2-4x+6.
