人教版七年级上册数学第二章整式的加减课件-小结复习(一)(20张ppt)
文档属性
| 名称 | 人教版七年级上册数学第二章整式的加减课件-小结复习(一)(20张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 343.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 10:34:01 | ||
图片预览








文档简介
(共20张PPT)
小结复习(一)
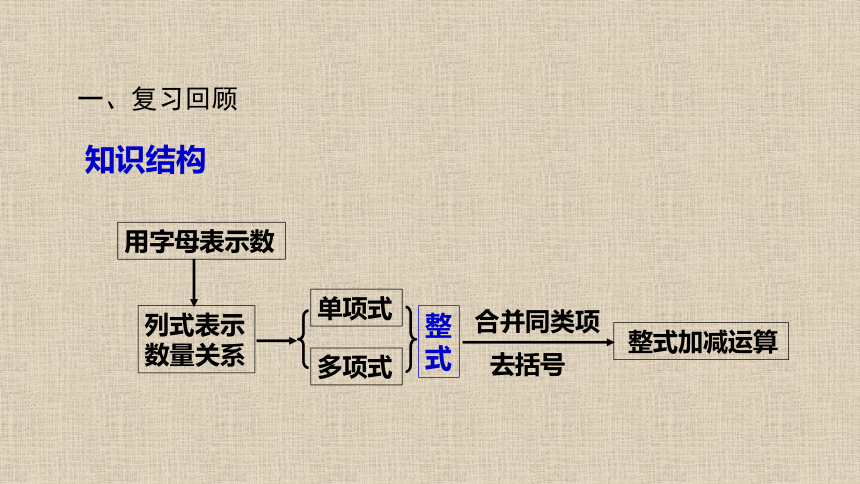
用字母表示数
列式表示数量关系
单项式
多项式
整式
整式加减运算
合并同类项
去括号
知识结构
一、复习回顾
一、复习回顾
单项式:
表示数或字母的积的式子叫做单项式 . 单独的一个数或一个字母也是单项式 . 单项式中的数字因数叫做这个单项式的系数,所有字母的指数的和叫做这个单项式的次数.
例如,单项式 的系数分别是 __________,次数分别是_________.
一、复习回顾
多项式:
几个单项式的和叫做多项式 . 其中,每个单项式叫 多项式的项,不含字母的项叫做常数项 . 多项式里,次数最高项的次数叫做这个多项式的次数.
例如, 的项是 ____________,其中,常数项是 ___.
的次数是 ____,它是 _____________;
的次数是 ____,它是 _____________.
四次三项式
二次二项式
二、典型例题
例 列式表示:
(1) 边长为 a cm的正方形的周长可表示为_______cm.
(2) 一个三位数,百位数字为 a,十位数字为 b,个位数字为 c,则这个三位数可表示为 _______________.
此处乘号“×”
通常省略不写.
二、典型例题
例 列式表示:
(3) 已知轮船在静水中前进的速度是 m 千米/时,水流的速度是2千米/时,若轮船顺水航行3小时,再逆水航行2小时,共航行_____________千米.
此处应加上括号
分析: v顺流= v船+ v水 ; v逆流= v船- v水 .
二、典型例题
例 列式表示:
分析:先明确进价、标价、实际售价的关系
①标价=进价×(1+x%)
②售价=标价×折扣
(4) 一种商品每件进价为 a 元,若按进价提高30%标价,再按标价的八五折出售,那么每件商品的售价是 _______________ 元. (用含a的式子表示)
二、典型例题
例 列式表示:
(5) 如图是一所住宅的建筑平面图(图中长度单位:m),
用式子表示这所住宅的建筑面积为________________m .
分析:先将4个长方形的面积分别表示,再相加即可.
按字母 x 的指数从大到小(降幂)排列
解:
二、典型例题
例 列式表示:
分析:阴影面积等于大圆面积减去小圆面积 .
(6) 如图,大圆的半径为R,小圆的面积是大圆面积的 ,则阴影部分的面积为_________.
o
R
小结:列式时书写应注意什么?
注意书写规范:
1. 当数字与字母相乘或是字母与字母相乘时,出现的乘号通常写成 “·”
或省略不写;
2. 数字与字母相乘时,数字写在字母
的前面;
3. 除法运算写成分数形式;
4. 若系数是“ ”或“1”,则 1 常省略不写;
带分数与字母相乘时,系数要化成假分数.
观察下列各式,哪些是单项式?哪些是多项式?
系数是 ,次数是 2;
一次三项式;
一次二项式;
二次三项式.
是单项式的指出系数和次数,是多项式的指出是几次几项式?
系数是 ,次数是 1;
系数是4 ,次数是 1;
二、典型例题
试一试:
(1) 请赋予单项式“4a”一个实际含义: ______________.
(2)请赋予多项式“100a+10b+c”一个实际含义: ______________.
分析:此类题目答案不唯一,只要符合实际意义即可.
二、典型例题
试一试:
(1) 请赋予单项式“4a”一个实际含义: ______________.
①一箱苹果重 a kg,4箱苹果重 4a kg.
②开学前小明买了4个练习本,每本 a 元,他共花费了4a 元.
③一个长方形的长是a cm,宽是4 cm,则这个长方形的面积是 4a .
二、典型例题
试一试:
(2) 请赋予多项式“100a+10b+c”一个实际含义: ______________.
② 学校体育组采购一批运动器材,买一副乒乓球拍需要100元,一副球网10元,一个乒乓球需要1元,买 a 副球拍、b 副球网、c 个乒乓球共需要 元.
① 大米、食油、食盐的单价分别是为 a元/千克,b元/千克,c元/千克,买100千克大米、10千克食油、 1千克食盐共需 元 .
二、典型例题
三、课堂练习
练习1 列式表示:
(1) 棱长为 a cm的正方体的表面积可表示为______ cm ;
(2) 一个数比 t 的2倍小5,则这个数为 ___________;
(3) 数 y 的立方的相反数是___________;
练习1 列式表示:
(4)某班有 x 名学生,现把一批图书分给全班学生阅读,如果每人分4本,还缺25本,则这批图书共____________本;
(5)买单价 c 元的商品 b 件,支付100元,应找回___________元.
两处应加上括号
三、课堂练习
练习2 在下列整式中,
单项式是______________,系数分别是 ______,次数分别是____,
多项式是______________________________,分别是几次几项式?
答: 是一次二项式, 是二次二项式, 是二次三项式.
三、课堂练习
1. 在列式时,书写应规范、准确
如: ① 当数字与字母相乘或是字母与字母相乘时,出现的乘号通常写成 “·”或省略不写;
② 数字与字母相乘时,数字写在字母的前面;
四、课堂小结
③ 若系数是“ ”或“1”,则 1 常省略不写;
④ 带分数与字母相乘时,系数要化成假分数等.
2. 整式的相关概念
四、课堂小结
次数: 所有字母的指数的和.
系数:单项式中的数字因数.
项:多项式中的每个单项式.
次数:多项式里,次数最高项的次数.
整式
单项式
多项式
注意:通常把一个多项式的各项按照某个字母的指数从大到小
(降幂)或者从小到大(升幂)的顺序排列.
思考
大众超市出售一种商品,其原价为a元,现有三种调价方案:(1)先提价20%,再降价20%; (2) 先降价20%,再提价20%;(3)先提价15%,再降价15%. 问用这三种方案调价,结果是否一样?最后是不是都恢复了原价
小结复习(一)
用字母表示数
列式表示数量关系
单项式
多项式
整式
整式加减运算
合并同类项
去括号
知识结构
一、复习回顾
一、复习回顾
单项式:
表示数或字母的积的式子叫做单项式 . 单独的一个数或一个字母也是单项式 . 单项式中的数字因数叫做这个单项式的系数,所有字母的指数的和叫做这个单项式的次数.
例如,单项式 的系数分别是 __________,次数分别是_________.
一、复习回顾
多项式:
几个单项式的和叫做多项式 . 其中,每个单项式叫 多项式的项,不含字母的项叫做常数项 . 多项式里,次数最高项的次数叫做这个多项式的次数.
例如, 的项是 ____________,其中,常数项是 ___.
的次数是 ____,它是 _____________;
的次数是 ____,它是 _____________.
四次三项式
二次二项式
二、典型例题
例 列式表示:
(1) 边长为 a cm的正方形的周长可表示为_______cm.
(2) 一个三位数,百位数字为 a,十位数字为 b,个位数字为 c,则这个三位数可表示为 _______________.
此处乘号“×”
通常省略不写.
二、典型例题
例 列式表示:
(3) 已知轮船在静水中前进的速度是 m 千米/时,水流的速度是2千米/时,若轮船顺水航行3小时,再逆水航行2小时,共航行_____________千米.
此处应加上括号
分析: v顺流= v船+ v水 ; v逆流= v船- v水 .
二、典型例题
例 列式表示:
分析:先明确进价、标价、实际售价的关系
①标价=进价×(1+x%)
②售价=标价×折扣
(4) 一种商品每件进价为 a 元,若按进价提高30%标价,再按标价的八五折出售,那么每件商品的售价是 _______________ 元. (用含a的式子表示)
二、典型例题
例 列式表示:
(5) 如图是一所住宅的建筑平面图(图中长度单位:m),
用式子表示这所住宅的建筑面积为________________m .
分析:先将4个长方形的面积分别表示,再相加即可.
按字母 x 的指数从大到小(降幂)排列
解:
二、典型例题
例 列式表示:
分析:阴影面积等于大圆面积减去小圆面积 .
(6) 如图,大圆的半径为R,小圆的面积是大圆面积的 ,则阴影部分的面积为_________.
o
R
小结:列式时书写应注意什么?
注意书写规范:
1. 当数字与字母相乘或是字母与字母相乘时,出现的乘号通常写成 “·”
或省略不写;
2. 数字与字母相乘时,数字写在字母
的前面;
3. 除法运算写成分数形式;
4. 若系数是“ ”或“1”,则 1 常省略不写;
带分数与字母相乘时,系数要化成假分数.
观察下列各式,哪些是单项式?哪些是多项式?
系数是 ,次数是 2;
一次三项式;
一次二项式;
二次三项式.
是单项式的指出系数和次数,是多项式的指出是几次几项式?
系数是 ,次数是 1;
系数是4 ,次数是 1;
二、典型例题
试一试:
(1) 请赋予单项式“4a”一个实际含义: ______________.
(2)请赋予多项式“100a+10b+c”一个实际含义: ______________.
分析:此类题目答案不唯一,只要符合实际意义即可.
二、典型例题
试一试:
(1) 请赋予单项式“4a”一个实际含义: ______________.
①一箱苹果重 a kg,4箱苹果重 4a kg.
②开学前小明买了4个练习本,每本 a 元,他共花费了4a 元.
③一个长方形的长是a cm,宽是4 cm,则这个长方形的面积是 4a .
二、典型例题
试一试:
(2) 请赋予多项式“100a+10b+c”一个实际含义: ______________.
② 学校体育组采购一批运动器材,买一副乒乓球拍需要100元,一副球网10元,一个乒乓球需要1元,买 a 副球拍、b 副球网、c 个乒乓球共需要 元.
① 大米、食油、食盐的单价分别是为 a元/千克,b元/千克,c元/千克,买100千克大米、10千克食油、 1千克食盐共需 元 .
二、典型例题
三、课堂练习
练习1 列式表示:
(1) 棱长为 a cm的正方体的表面积可表示为______ cm ;
(2) 一个数比 t 的2倍小5,则这个数为 ___________;
(3) 数 y 的立方的相反数是___________;
练习1 列式表示:
(4)某班有 x 名学生,现把一批图书分给全班学生阅读,如果每人分4本,还缺25本,则这批图书共____________本;
(5)买单价 c 元的商品 b 件,支付100元,应找回___________元.
两处应加上括号
三、课堂练习
练习2 在下列整式中,
单项式是______________,系数分别是 ______,次数分别是____,
多项式是______________________________,分别是几次几项式?
答: 是一次二项式, 是二次二项式, 是二次三项式.
三、课堂练习
1. 在列式时,书写应规范、准确
如: ① 当数字与字母相乘或是字母与字母相乘时,出现的乘号通常写成 “·”或省略不写;
② 数字与字母相乘时,数字写在字母的前面;
四、课堂小结
③ 若系数是“ ”或“1”,则 1 常省略不写;
④ 带分数与字母相乘时,系数要化成假分数等.
2. 整式的相关概念
四、课堂小结
次数: 所有字母的指数的和.
系数:单项式中的数字因数.
项:多项式中的每个单项式.
次数:多项式里,次数最高项的次数.
整式
单项式
多项式
注意:通常把一个多项式的各项按照某个字母的指数从大到小
(降幂)或者从小到大(升幂)的顺序排列.
思考
大众超市出售一种商品,其原价为a元,现有三种调价方案:(1)先提价20%,再降价20%; (2) 先降价20%,再提价20%;(3)先提价15%,再降价15%. 问用这三种方案调价,结果是否一样?最后是不是都恢复了原价
