5.2.2平行线的判定课件2021-2022学年人教版七年级数学下册(35张ppt)
文档属性
| 名称 | 5.2.2平行线的判定课件2021-2022学年人教版七年级数学下册(35张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 00:00:00 | ||
图片预览




文档简介
(共35张PPT)
5.2.2 平行线的判定
学习目标
1
2
经历“同位角相等,两直线平行”的发现过程
掌握平行线的判定方法
3
灵活利用平行线的三个判断方法解决有关的问题
学习重难点
重点
难点
掌握平行线的三个判定方法
灵活利用平行线的三个判断方法解决有关的问题
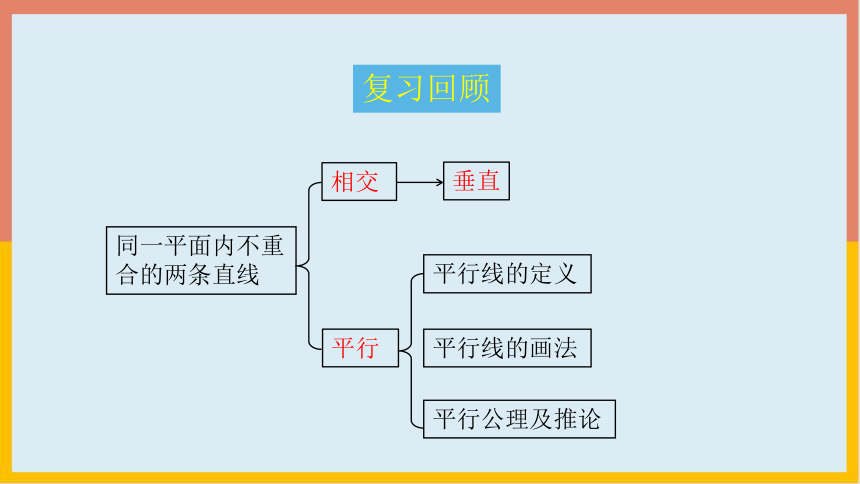
平行
相交
平行线的定义
平行线的画法
平行公理及推论
同一平面内不重合的两条直线
垂直
复习回顾
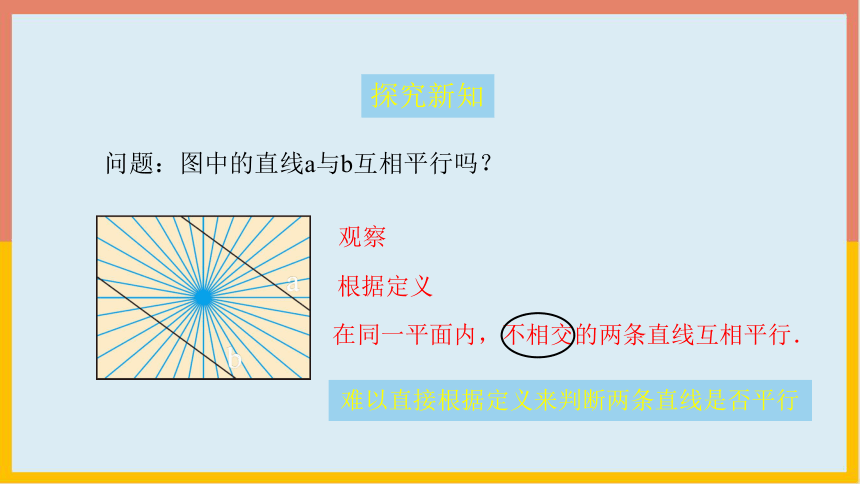
问题:图中的直线a与b互相平行吗?
a
b
探究新知
在同一平面内,不相交的两条直线互相平行.
观察
根据定义
难以直接根据定义来判断两条直线是否平行
还有什么方法能判断两条直线是否平行?
A
B
C
D
如果AB∥EF,那么AB∥CD .
问题没有解决!
E
F
如何判断?
再画一条与CD平行的直线EF,
寻求新方法
知识和经验
B
C
A
D
O
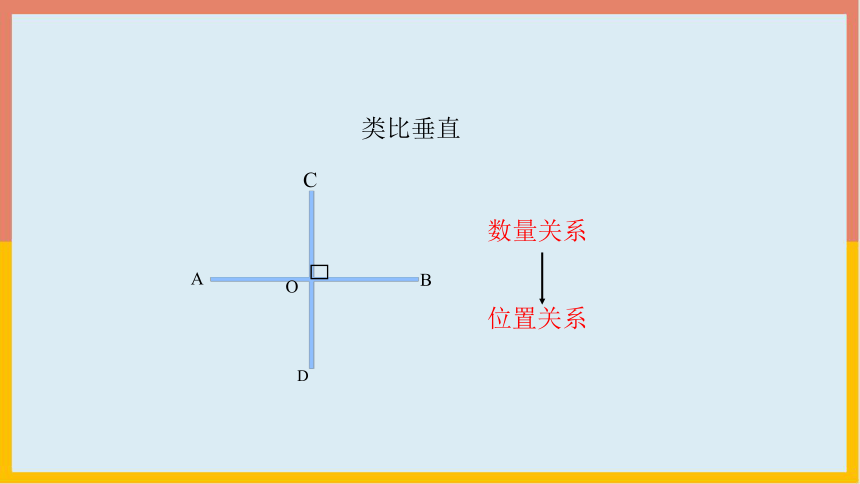
类比垂直
数量关系
位置关系
a
c
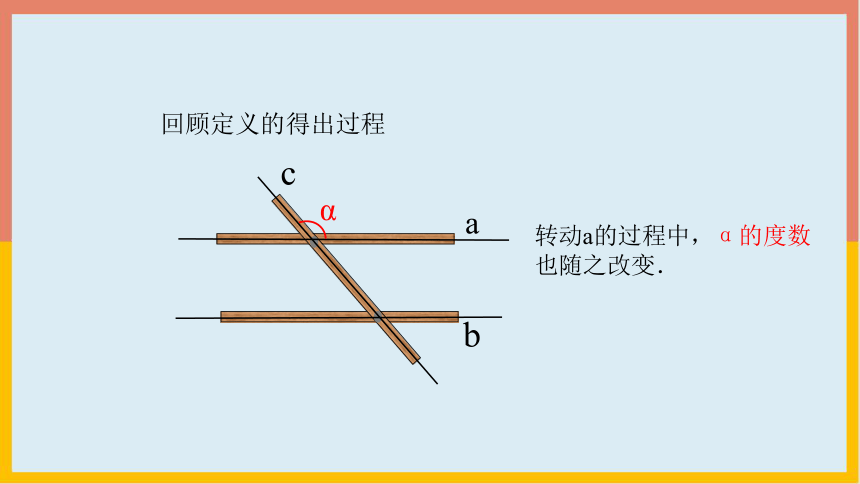
回顾定义的得出过程
b
α
c
回顾定义的得出过程
a
b
转动a的过程中,α的度数也随之改变.
A
B
C
D
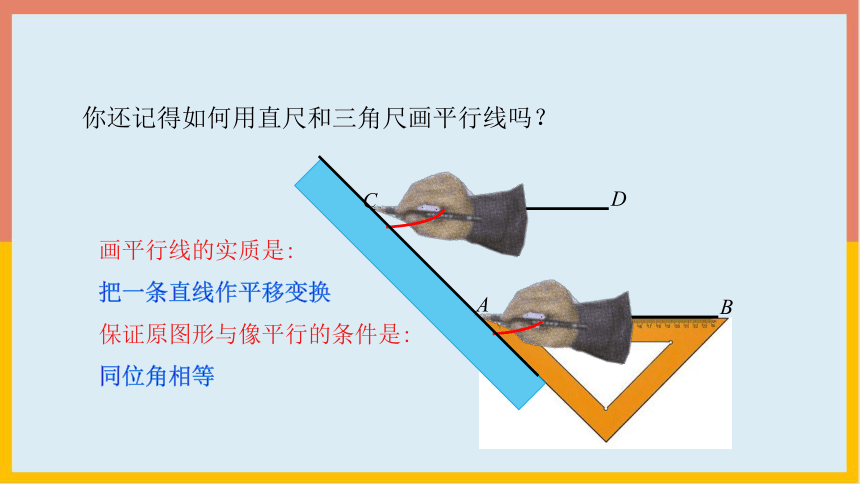
你还记得如何用直尺和三角尺画平行线吗?
画平行线的实质是:
把一条直线作平移变换
保证原图形与像平行的条件是:
同位角相等
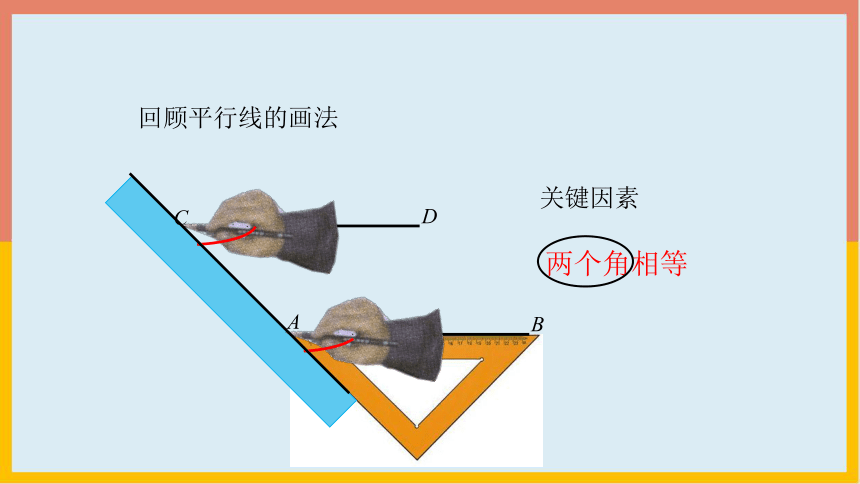
回顾平行线的画法
关键因素
两个角相等
A
B
C
D
A
B
E
F
G
1
C
D
2
H
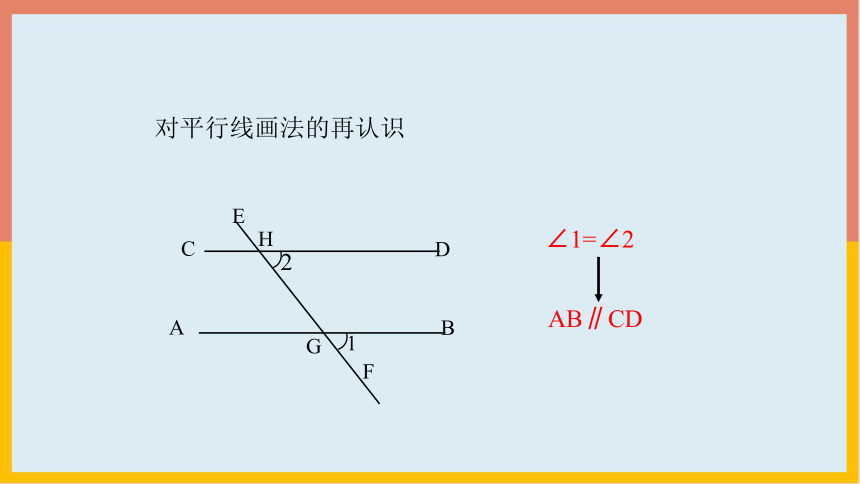
对平行线画法的再认识
∠1=∠2
AB∥CD
判定方法1 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
同位角相等,两直线平行.
简单说成:
A
B
E
F
G
1
C
D
2
H
∠1=∠2
a∥b
因为∠1=∠2,
所以a∥b.
c
a
b
2
1
推理过程:
∠1和∠2是同位角
判定方法1 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
定义
判定
类比垂直
猜想
画平行线
判定方法
难以实现
发现问题
思路梳理
引入截线
借助同位角
思考:有没有其他的判定方法?
再探新知
a
b
c
同位角、内错角、同旁内角
两条直线被第三条直线所截
思考:有没有其他的判定方法?
c
a
b
3
2
1
4
∠2和∠3是内错角
∠4和∠2是同旁内角
如果∠2=∠3,
能得出a∥b吗?
思考:有没有其他的判定方法?
c
a
b
2
3
猜想:如果∠2=∠3,则a∥b.
∠3=∠1
∠2=∠3
∠1=∠2
a∥b
猜想:如果∠2=∠3,则a∥b.
c
a
b
2
1
3
因为∠2=∠3,而∠3=∠1,
推理得出结论
所以∠1=∠2.
从而a∥b.
c
a
b
2
1
3
判定方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
内错角相等,两直线平行.
简单说成:
c
a
b
2
1
3
如图,
因为∠2=∠3,
所以a∥b.
内错角相等,两直线平行.
新问题
已解决的问题
转化
同位角相等,两直线平行.
提出问题
得出结论
猜想
推理
思路梳理
如图,∠2和∠4是一对同旁内角.
思考:它们满足怎样的数量关系时能判断a∥b?
再探新知
c
a
b
2
1
3
4
推理过程
因为∠2+∠4=180°,∠4+∠1=180°,
从而a∥b.
所以∠1=∠2 .
c
a
b
2
1
3
4
判定方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:
同旁内角互补,两直线平行.
c
a
b
2
1
3
4
如图,
因为∠4+∠2=180°,
所以a∥b.
已知∠2+∠4=180°
?
a∥b
∠3=∠2
再探新知
能否利用“内错角相等,两直线平行”得到判定方法3呢?
c
a
b
2
1
3
4
推理过程
所以∠3=∠2.
所以a∥b.
因为∠2+∠4=180°,∠3+∠4=180°,
c
a
b
2
1
3
4
提出问题
得出结论
猜想
推理
已知∠2+∠4=180°
a∥b
∠1=∠2
或∠3=∠2
∠3+∠4=180°
∠4+∠1=180°
思路梳理
c
a
b
2
1
3
4
同位角相等
内错角相等
同旁内角互补
两直线平行
平行线的判定
角的数量关系
直线的位置关系
归纳总结
问题1 如图,你能说出木工用图中的角尺画平行线的道理吗?
解决问题
A
B
C
D
E
F
用角尺画平行线实际上是画出了两个直角,根据“同位角相等(也可以根据内错角相等,同旁内角互补),两直线平行”,这样画出的就是平行线.
A
D
B
E
C
O
问题2 如图,为了加固房屋,要在屋架上加一根横梁DE,
使DE∥BC,如果∠ABC=31°,∠ADE应为多少度?
D
B
E
C
A
角的数量关系
∠ABC=∠ADE
同位角
DE∥BC
答:∠ADE应为31°.
课堂小结
平行线的判定方法
同位角相等, 两直线平行.
内错角相等, 两直线平行.
同旁内角互补,两直线平行.
特殊位置的角的数量关系
条件
1.如图,这是小明同学自己制作的英语抄写纸的一部分,其中的横格线互相平行吗?你有多少种判别方法?
课后作业
2.通过本节课的学习,你觉得最大的收获是什么?遇到新问题时我们可以如何解决呢?
课后作业
再 见
5.2.2 平行线的判定
学习目标
1
2
经历“同位角相等,两直线平行”的发现过程
掌握平行线的判定方法
3
灵活利用平行线的三个判断方法解决有关的问题
学习重难点
重点
难点
掌握平行线的三个判定方法
灵活利用平行线的三个判断方法解决有关的问题
平行
相交
平行线的定义
平行线的画法
平行公理及推论
同一平面内不重合的两条直线
垂直
复习回顾
问题:图中的直线a与b互相平行吗?
a
b
探究新知
在同一平面内,不相交的两条直线互相平行.
观察
根据定义
难以直接根据定义来判断两条直线是否平行
还有什么方法能判断两条直线是否平行?
A
B
C
D
如果AB∥EF,那么AB∥CD .
问题没有解决!
E
F
如何判断?
再画一条与CD平行的直线EF,
寻求新方法
知识和经验
B
C
A
D
O
类比垂直
数量关系
位置关系
a
c
回顾定义的得出过程
b
α
c
回顾定义的得出过程
a
b
转动a的过程中,α的度数也随之改变.
A
B
C
D
你还记得如何用直尺和三角尺画平行线吗?
画平行线的实质是:
把一条直线作平移变换
保证原图形与像平行的条件是:
同位角相等
回顾平行线的画法
关键因素
两个角相等
A
B
C
D
A
B
E
F
G
1
C
D
2
H
对平行线画法的再认识
∠1=∠2
AB∥CD
判定方法1 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
同位角相等,两直线平行.
简单说成:
A
B
E
F
G
1
C
D
2
H
∠1=∠2
a∥b
因为∠1=∠2,
所以a∥b.
c
a
b
2
1
推理过程:
∠1和∠2是同位角
判定方法1 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
定义
判定
类比垂直
猜想
画平行线
判定方法
难以实现
发现问题
思路梳理
引入截线
借助同位角
思考:有没有其他的判定方法?
再探新知
a
b
c
同位角、内错角、同旁内角
两条直线被第三条直线所截
思考:有没有其他的判定方法?
c
a
b
3
2
1
4
∠2和∠3是内错角
∠4和∠2是同旁内角
如果∠2=∠3,
能得出a∥b吗?
思考:有没有其他的判定方法?
c
a
b
2
3
猜想:如果∠2=∠3,则a∥b.
∠3=∠1
∠2=∠3
∠1=∠2
a∥b
猜想:如果∠2=∠3,则a∥b.
c
a
b
2
1
3
因为∠2=∠3,而∠3=∠1,
推理得出结论
所以∠1=∠2.
从而a∥b.
c
a
b
2
1
3
判定方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
内错角相等,两直线平行.
简单说成:
c
a
b
2
1
3
如图,
因为∠2=∠3,
所以a∥b.
内错角相等,两直线平行.
新问题
已解决的问题
转化
同位角相等,两直线平行.
提出问题
得出结论
猜想
推理
思路梳理
如图,∠2和∠4是一对同旁内角.
思考:它们满足怎样的数量关系时能判断a∥b?
再探新知
c
a
b
2
1
3
4
推理过程
因为∠2+∠4=180°,∠4+∠1=180°,
从而a∥b.
所以∠1=∠2 .
c
a
b
2
1
3
4
判定方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:
同旁内角互补,两直线平行.
c
a
b
2
1
3
4
如图,
因为∠4+∠2=180°,
所以a∥b.
已知∠2+∠4=180°
?
a∥b
∠3=∠2
再探新知
能否利用“内错角相等,两直线平行”得到判定方法3呢?
c
a
b
2
1
3
4
推理过程
所以∠3=∠2.
所以a∥b.
因为∠2+∠4=180°,∠3+∠4=180°,
c
a
b
2
1
3
4
提出问题
得出结论
猜想
推理
已知∠2+∠4=180°
a∥b
∠1=∠2
或∠3=∠2
∠3+∠4=180°
∠4+∠1=180°
思路梳理
c
a
b
2
1
3
4
同位角相等
内错角相等
同旁内角互补
两直线平行
平行线的判定
角的数量关系
直线的位置关系
归纳总结
问题1 如图,你能说出木工用图中的角尺画平行线的道理吗?
解决问题
A
B
C
D
E
F
用角尺画平行线实际上是画出了两个直角,根据“同位角相等(也可以根据内错角相等,同旁内角互补),两直线平行”,这样画出的就是平行线.
A
D
B
E
C
O
问题2 如图,为了加固房屋,要在屋架上加一根横梁DE,
使DE∥BC,如果∠ABC=31°,∠ADE应为多少度?
D
B
E
C
A
角的数量关系
∠ABC=∠ADE
同位角
DE∥BC
答:∠ADE应为31°.
课堂小结
平行线的判定方法
同位角相等, 两直线平行.
内错角相等, 两直线平行.
同旁内角互补,两直线平行.
特殊位置的角的数量关系
条件
1.如图,这是小明同学自己制作的英语抄写纸的一部分,其中的横格线互相平行吗?你有多少种判别方法?
课后作业
2.通过本节课的学习,你觉得最大的收获是什么?遇到新问题时我们可以如何解决呢?
课后作业
再 见
