24.2.2直线和圆的位置关系及其判定课件2021-2022学年人教版数学九年级上册(22张ppt)
文档属性
| 名称 | 24.2.2直线和圆的位置关系及其判定课件2021-2022学年人教版数学九年级上册(22张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 00:00:00 | ||
图片预览



文档简介
(共22张PPT)
直线和圆的位置关系及其判定
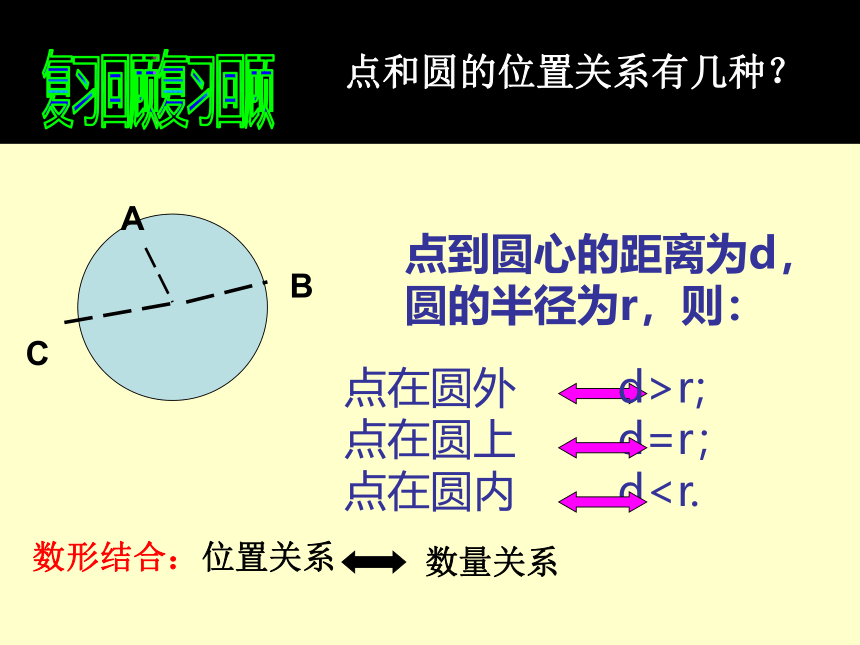
点和圆的位置关系有几种?
点到圆心的距离为d,圆的半径为r,则:
复习回顾
点在圆外 d>r;
点在圆上 d=r;
点在圆内 dA
B
C
位置关系
数形结合:
数量关系
今天老师和同学们一起来探究
直线与圆的位置关系(一)
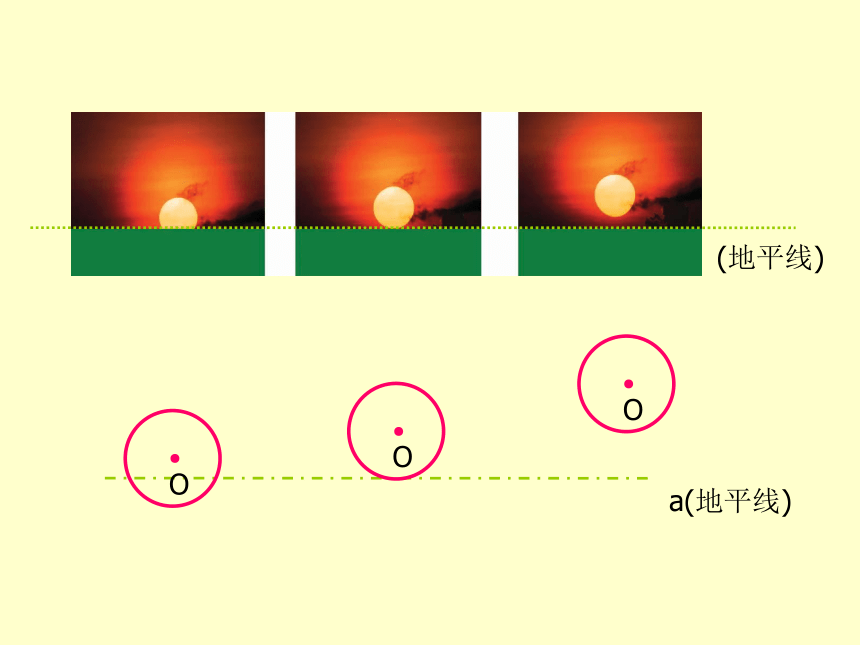
请同学们利用手中的工具再现海上日出的整个情景。
在再现过程中,你认为直线与圆的位置关系可以分为哪几类?
你分类的依据是什么?
操作与思考
(地平线)
a(地平线)
●O
●O
●O
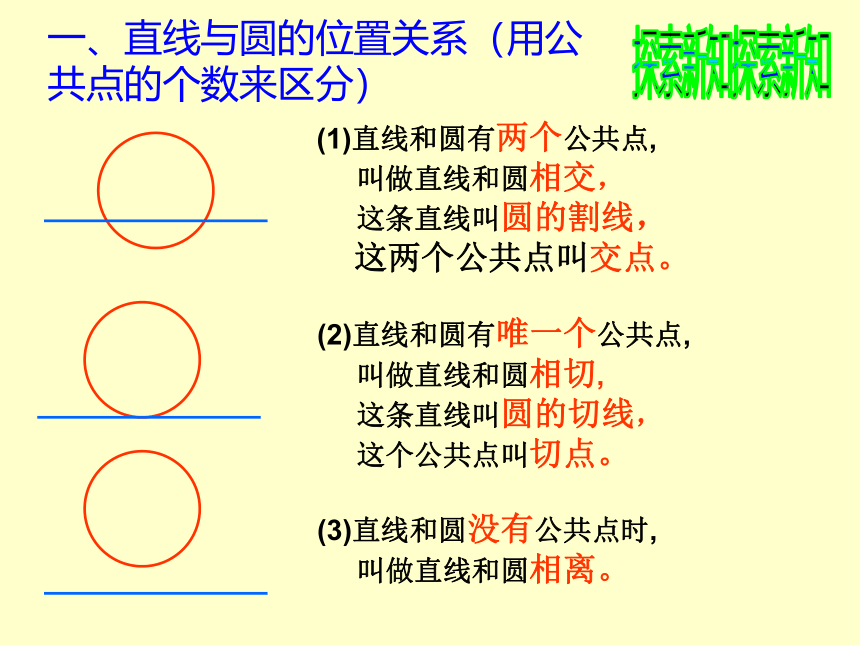
(2)直线和圆有唯一个公共点,
叫做直线和圆相切,
这条直线叫圆的切线,
这个公共点叫切点。
(1)直线和圆有两个公共点,
叫做直线和圆相交,
这条直线叫圆的割线,
这两个公共点叫交点。
(3)直线和圆没有公共点时,
叫做直线和圆相离。
一、直线与圆的位置关系(用公共点的个数来区分)
探索新知
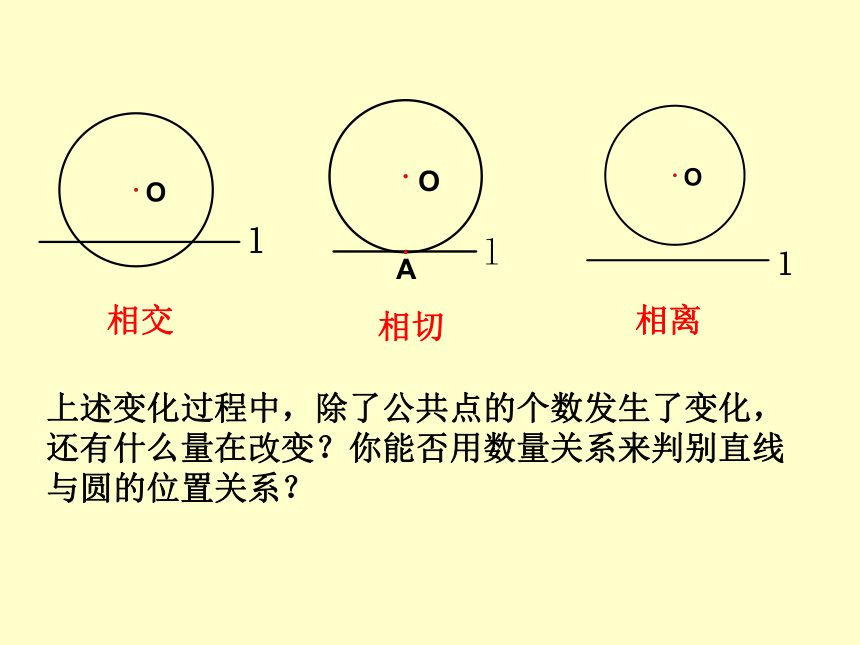
相交
相切
相离
上述变化过程中,除了公共点的个数发生了变化,还有什么量在改变?你能否用数量关系来判别直线与圆的位置关系?
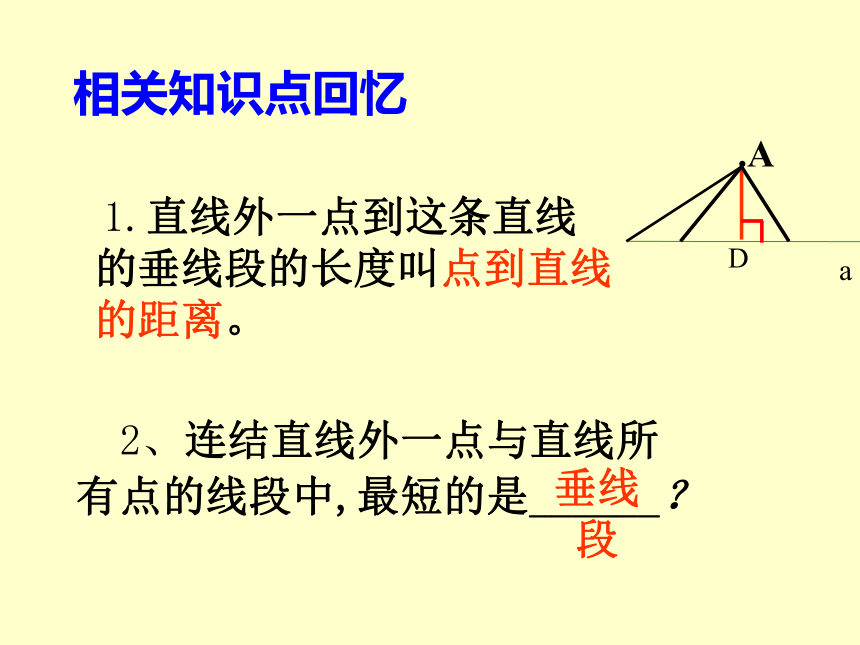
2、连结直线外一点与直线所
有点的线段中,最短的是______?
1.直线外一点到这条直线
的垂线段的长度叫点到直线
的距离。
垂线段
a
.A
D
相关知识点回忆
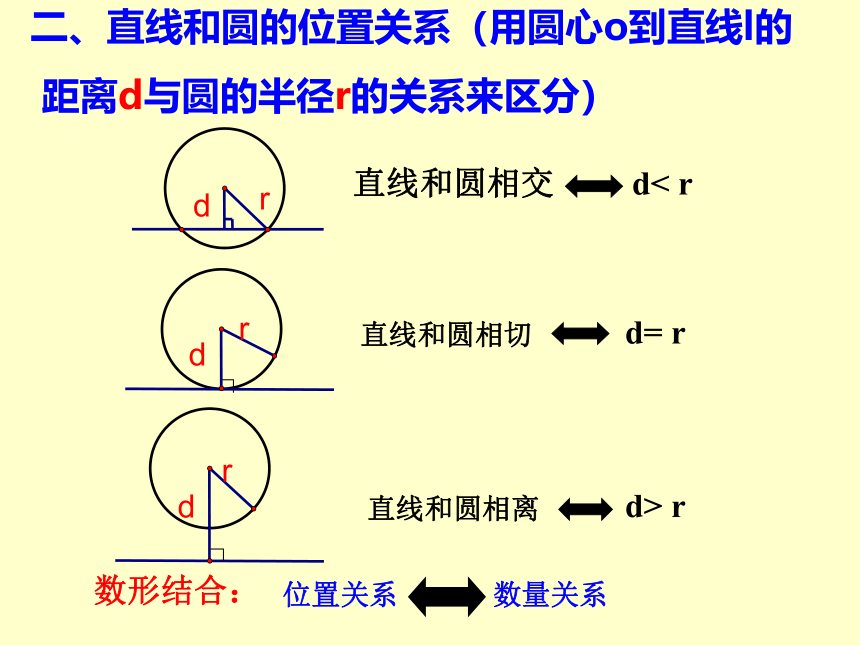
直线和圆相交
d< r
直线和圆相切
d= r
直线和圆相离
d> r
r
d
∟
r
d
∟
r
d
数形结合:
位置关系
数量关系
二、直线和圆的位置关系(用圆心o到直线l的
距离d与圆的半径r的关系来区分)
总结:
判定直线 与圆的位置关系的方法有____种:
(1)根据定义,由________________
的个数来判断;
(2)根据性质,由_________________ 的关系来判断。
在实际应用中,常采用第二种方法判定。
两
直线 与圆的公共点
圆心到直线的距离d与半径r
1、已知圆的直径为13cm,设直线和圆心的距离为d :
3)若d= 8 cm ,则直线与圆______, 直线与圆有____个公共点.
2)若d=6.5cm ,则直线与圆______, 直线与圆有____个公共点.
1)若d=4.5cm ,则直线与圆 , 直线与圆有____个公共点.
3)若AB和⊙O相交,则 .
2、已知⊙O的半径为5cm, 圆心O与直线AB的距离为d, 根据 条件填写d的范围:
1)若AB和⊙O相离, 则 ;
2)若AB和⊙O相切, 则 ;
相交
相切
相离
d > 5cm
d = 5cm
d < 5cm
小试牛刀
0cm≤
2
1
0
3、如图,在Rt△ABC中,∠C=90°,AB=5cm,
AC=3cm,以C为圆心的圆与AB
相切,则这个圆的半径是 cm。
4、直线L 和⊙O有公共点,则直线L与⊙O( ).
A、相离;B、相切;C、相交;D、相切或相交。
12/5
D
B
C
A
4
3
例:在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB
有怎样的位置关系?为什么?
(1)r=2cm;(2)r=2.4cm (3)r=3cm.
B
C
A
4
3
D
d
解:过C作CD⊥AB,垂足为D
在△ABC中,
AB=
5
根据三角形的面积公式有
∴
即圆心C到AB的距离d=2.4cm
所以 (1)当r=2cm时,
有d>r,
因此⊙C和AB相离。
B
C
A
4
3
D
d
(2)当r=2.4cm时,
有d=r,
因此⊙C和AB相切。
(3)当r=3cm时,
有d因此,⊙C和AB相交。
B
C
A
4
3
D
B
C
A
4
3
D
d
d
2、如图,已知∠BAC=30度,M为AC 上一点,且AM=5cm,以M为圆心、 r为半径的圆与直线AB有怎样的 位置关系?为什么?
(1) r=2cm
(2) r=4cm
(3) r=2.5cm
D
M
A
B
C
A.(-3,-4)
O
x
y
已知⊙A的直径为6,点A的坐标为
(-3,-4),则x轴与⊙A的位置关系是_____, y轴与⊙A的位置关系是_____。
B
C
4
3
相离
相切
-1
-1
拓展
.(-3,-4)
O
x
y
B
C
4
3
-1
-1
若⊙A要与x轴相切,则⊙A该向上移动多少个单位?若⊙A要与x轴相交呢?
思考
讨论
在Rt△ABC中,∠C=90°,AC=5cm,BC=12cm,
以C为圆心,r为半径作圆。
①当r满足 时, 直线AB与⊙C相离。
②当r满足 时,直线AB与⊙C相切。
③当r满足 时,直线AB与⊙C相交。
0﹤r﹤
r=
r﹥
④当r满足 时,
线段AB与⊙C只有一个公共点。
或5﹤r≤12
r=
小结:1、直线与圆的位置关系:
0
d>r
1
d=r
切点
切线
2
d交点
割线
.O
l
d
r
┐
┐
.o
l
d
r
.O
l
d
┐
r
.
A
C
B
.
.
相离
相切
相交
2、判定直线 与圆的位置关系的方法有____种:
(1)根据定义,由__________________的个数来判断;
(2)根据性质,由_____________________ ______________的关系来判断。
在实际应用中,常采用第二种方法判定。
两
直线 与圆的公共点
圆心到直线的距离d
与半径r
知识像一艘船
让它载着我们
驶向理想的
……
谢谢
直线和圆的位置关系及其判定
点和圆的位置关系有几种?
点到圆心的距离为d,圆的半径为r,则:
复习回顾
点在圆外 d>r;
点在圆上 d=r;
点在圆内 d
B
C
位置关系
数形结合:
数量关系
今天老师和同学们一起来探究
直线与圆的位置关系(一)
请同学们利用手中的工具再现海上日出的整个情景。
在再现过程中,你认为直线与圆的位置关系可以分为哪几类?
你分类的依据是什么?
操作与思考
(地平线)
a(地平线)
●O
●O
●O
(2)直线和圆有唯一个公共点,
叫做直线和圆相切,
这条直线叫圆的切线,
这个公共点叫切点。
(1)直线和圆有两个公共点,
叫做直线和圆相交,
这条直线叫圆的割线,
这两个公共点叫交点。
(3)直线和圆没有公共点时,
叫做直线和圆相离。
一、直线与圆的位置关系(用公共点的个数来区分)
探索新知
相交
相切
相离
上述变化过程中,除了公共点的个数发生了变化,还有什么量在改变?你能否用数量关系来判别直线与圆的位置关系?
2、连结直线外一点与直线所
有点的线段中,最短的是______?
1.直线外一点到这条直线
的垂线段的长度叫点到直线
的距离。
垂线段
a
.A
D
相关知识点回忆
直线和圆相交
d< r
直线和圆相切
d= r
直线和圆相离
d> r
r
d
∟
r
d
∟
r
d
数形结合:
位置关系
数量关系
二、直线和圆的位置关系(用圆心o到直线l的
距离d与圆的半径r的关系来区分)
总结:
判定直线 与圆的位置关系的方法有____种:
(1)根据定义,由________________
的个数来判断;
(2)根据性质,由_________________ 的关系来判断。
在实际应用中,常采用第二种方法判定。
两
直线 与圆的公共点
圆心到直线的距离d与半径r
1、已知圆的直径为13cm,设直线和圆心的距离为d :
3)若d= 8 cm ,则直线与圆______, 直线与圆有____个公共点.
2)若d=6.5cm ,则直线与圆______, 直线与圆有____个公共点.
1)若d=4.5cm ,则直线与圆 , 直线与圆有____个公共点.
3)若AB和⊙O相交,则 .
2、已知⊙O的半径为5cm, 圆心O与直线AB的距离为d, 根据 条件填写d的范围:
1)若AB和⊙O相离, 则 ;
2)若AB和⊙O相切, 则 ;
相交
相切
相离
d > 5cm
d = 5cm
d < 5cm
小试牛刀
0cm≤
2
1
0
3、如图,在Rt△ABC中,∠C=90°,AB=5cm,
AC=3cm,以C为圆心的圆与AB
相切,则这个圆的半径是 cm。
4、直线L 和⊙O有公共点,则直线L与⊙O( ).
A、相离;B、相切;C、相交;D、相切或相交。
12/5
D
B
C
A
4
3
例:在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB
有怎样的位置关系?为什么?
(1)r=2cm;(2)r=2.4cm (3)r=3cm.
B
C
A
4
3
D
d
解:过C作CD⊥AB,垂足为D
在△ABC中,
AB=
5
根据三角形的面积公式有
∴
即圆心C到AB的距离d=2.4cm
所以 (1)当r=2cm时,
有d>r,
因此⊙C和AB相离。
B
C
A
4
3
D
d
(2)当r=2.4cm时,
有d=r,
因此⊙C和AB相切。
(3)当r=3cm时,
有d
B
C
A
4
3
D
B
C
A
4
3
D
d
d
2、如图,已知∠BAC=30度,M为AC 上一点,且AM=5cm,以M为圆心、 r为半径的圆与直线AB有怎样的 位置关系?为什么?
(1) r=2cm
(2) r=4cm
(3) r=2.5cm
D
M
A
B
C
A.(-3,-4)
O
x
y
已知⊙A的直径为6,点A的坐标为
(-3,-4),则x轴与⊙A的位置关系是_____, y轴与⊙A的位置关系是_____。
B
C
4
3
相离
相切
-1
-1
拓展
.(-3,-4)
O
x
y
B
C
4
3
-1
-1
若⊙A要与x轴相切,则⊙A该向上移动多少个单位?若⊙A要与x轴相交呢?
思考
讨论
在Rt△ABC中,∠C=90°,AC=5cm,BC=12cm,
以C为圆心,r为半径作圆。
①当r满足 时, 直线AB与⊙C相离。
②当r满足 时,直线AB与⊙C相切。
③当r满足 时,直线AB与⊙C相交。
0﹤r﹤
r=
r﹥
④当r满足 时,
线段AB与⊙C只有一个公共点。
或5﹤r≤12
r=
小结:1、直线与圆的位置关系:
0
d>r
1
d=r
切点
切线
2
d
割线
.O
l
d
r
┐
┐
.o
l
d
r
.O
l
d
┐
r
.
A
C
B
.
.
相离
相切
相交
2、判定直线 与圆的位置关系的方法有____种:
(1)根据定义,由__________________的个数来判断;
(2)根据性质,由_____________________ ______________的关系来判断。
在实际应用中,常采用第二种方法判定。
两
直线 与圆的公共点
圆心到直线的距离d
与半径r
知识像一艘船
让它载着我们
驶向理想的
……
谢谢
同课章节目录
