24.2.1点和圆的位置关系(共2课时)
文档属性
| 名称 | 24.2.1点和圆的位置关系(共2课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-31 00:00:00 | ||
图片预览





文档简介
课件42张PPT。24.2.1.1点和圆的位置关系 欢迎各位老师指导!1、圆周角等于它同弧所对的圆心角一半.一复习 圆周角的性质:2、同弧所对的圆周角都相等.在同圆或等圆中,3、同弦所对的圆周角相等或互补. 我国射击运动员在奥运会上屡获金牌,为我国赢得荣誉,右图是射击靶的示意图,它是由许多同心圆(圆心相同、半径不等的圆)构成的,你知道击中靶上不同位置的成绩是如何计算的吗? r问题二:
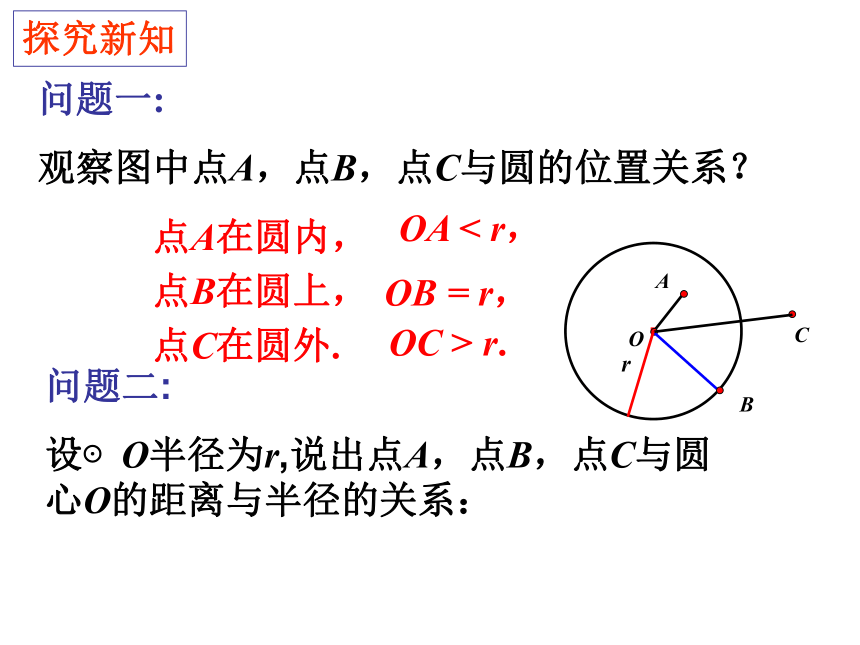
设⊙O半径为r,说出点A,点B,点C与圆心O的距离与半径的关系:·COABOC > r.问题一:
观察图中点A,点B,点C与圆的位置关系?点C在圆外.点A在圆内,点B在圆上,OA < r,OB = r,探究新知设⊙O的半径为r,点P到圆心的距离OP = d,则有:r·OA问题三:
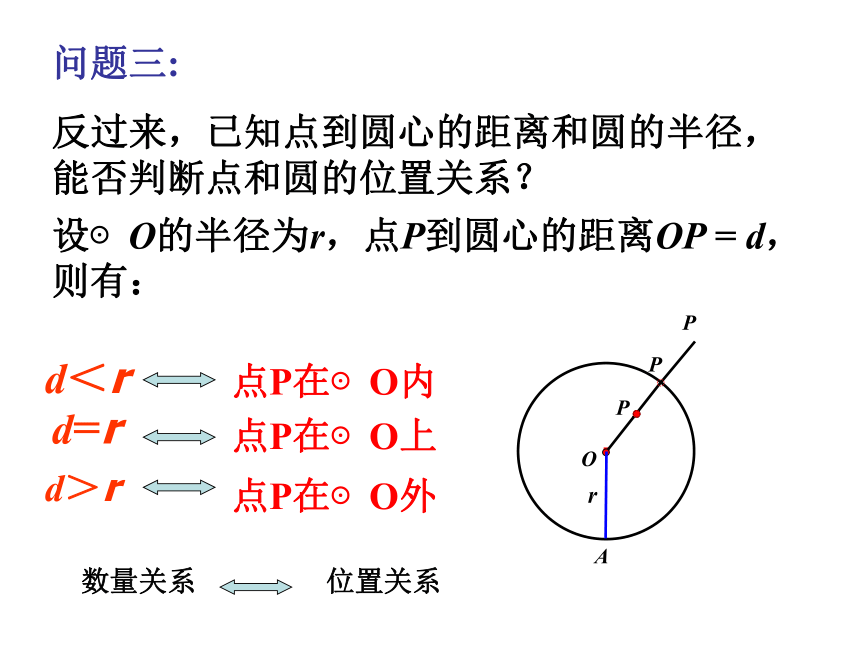
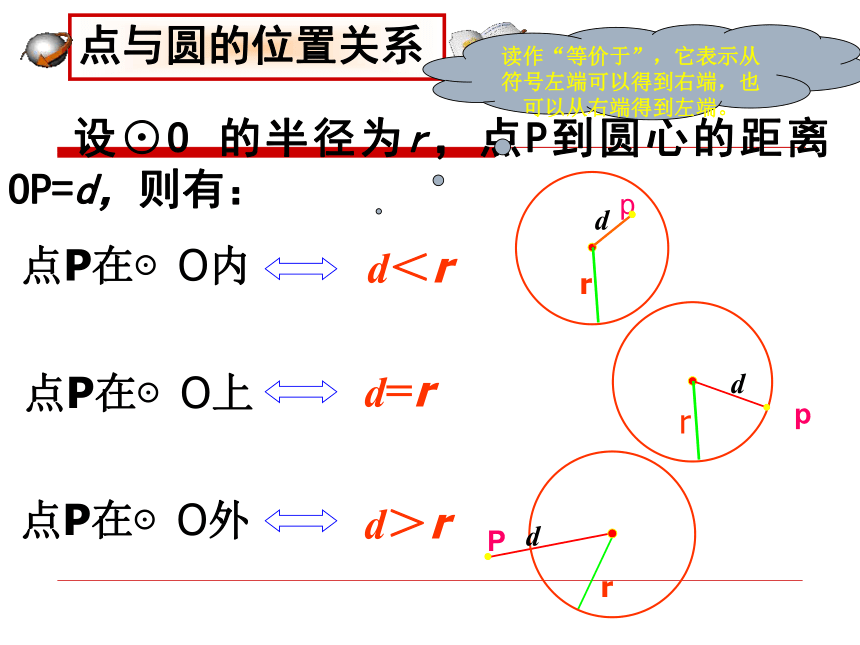
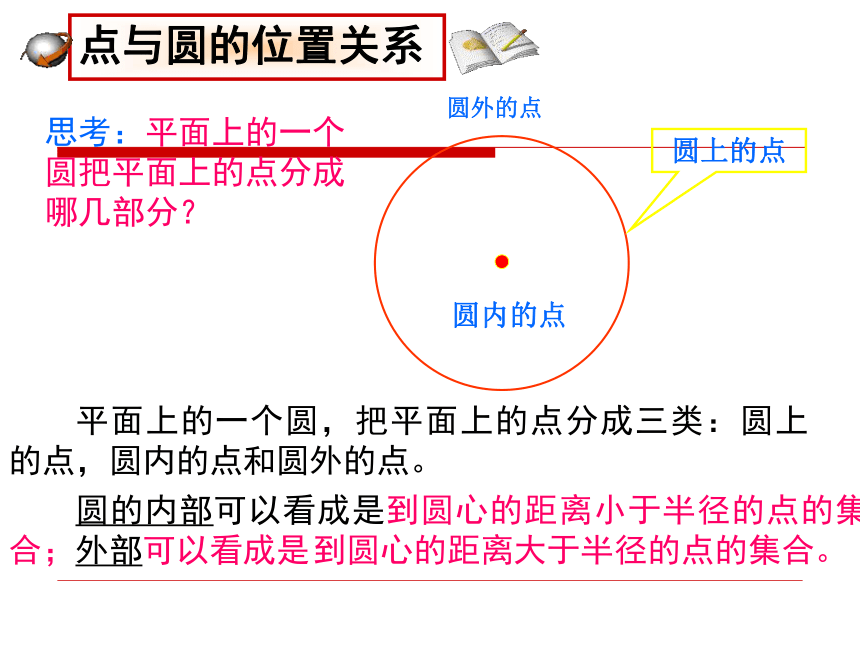
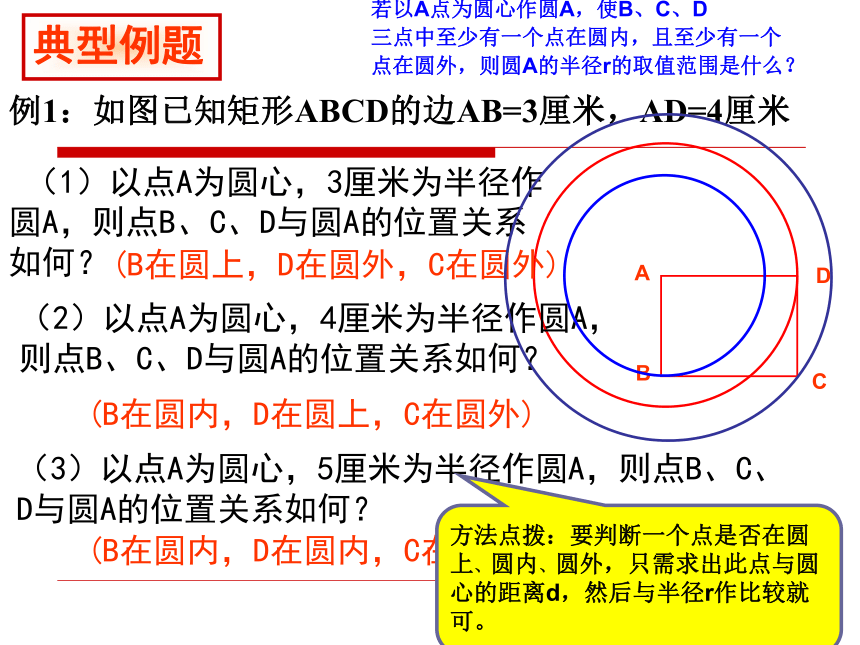
反过来,已知点到圆心的距离和圆的半径,能否判断点和圆的位置关系?PPP点A在⊙O内 d<r d=r d>r点B在⊙O上 点P在⊙O内点P在⊙O上点P在⊙O外 数量关系 位置关系 设⊙O 的半径为r,点P到圆心的距离OP=d,则有:点P在⊙O内 点P在⊙O上 点P在⊙O外 d<r d=r d>rd读作“等价于”,它表示从符号左端可以得到右端,也可以从右端得到左端。圆外的点圆内的点圆上的点 平面上的一个圆,把平面上的点分成三类:圆上的点,圆内的点和圆外的点。 圆的内部可以看成是到圆心的距离小于半径的点的集合;外部可以看成是 到圆心的距离大于半径的点的集合。思考:平面上的一个圆把平面上的点分成哪几部分? 射击靶图上,有一组以靶心为圆心的大小不同的圆,他们把靶图由内到外分成几个区域,这些区域用由高到底的环数来表示,射击成绩用弹着点位置对应的环数来表示.弹着点与靶心的距离决定了它在哪个圆内,弹着点离靶心越近,它所在的区域就越靠内,对应的环数也就越高,射击的成绩越好.你知道击中靶上不同位置的成绩是如何计算的吗 ?例1:如图已知矩形ABCD的边AB=3厘米,AD=4厘米 (1)以点A为圆心,3厘米为半径作圆A,则点B、C、D与圆A的位置关系如何? (B在圆上,D在圆外,C在圆外)(2)以点A为圆心,4厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?(B在圆内,D在圆上,C在圆外)(3)以点A为圆心,5厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?(B在圆内,D在圆内,C在圆上)若以A点为圆心作圆A,使B、C、D
三点中至少有一个点在圆内,且至少有一个
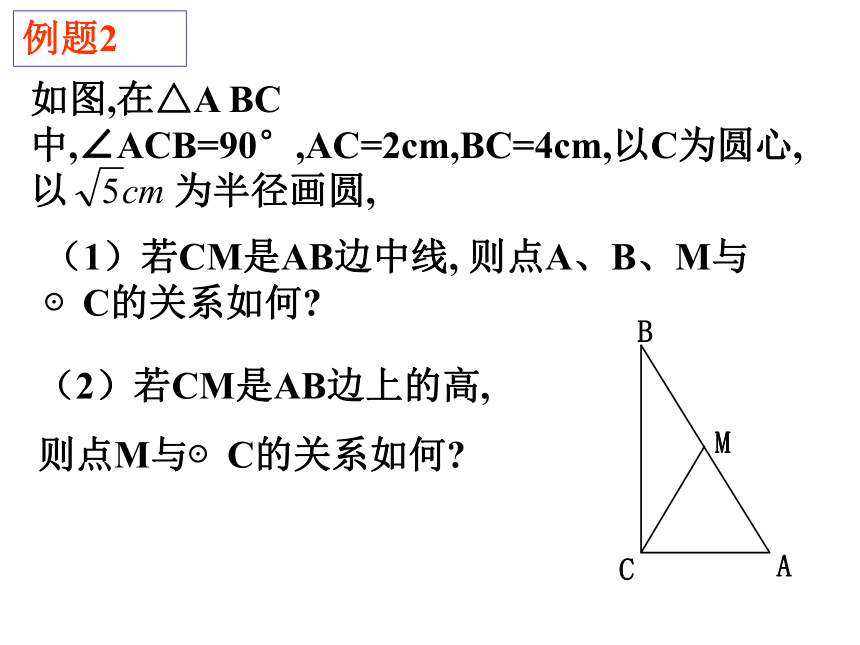
点在圆外,则圆A的半径r的取值范围是什么?例题2(1)若CM是AB边中线, 则点A、B、M与 ⊙C的关系如何?(2)若CM是AB边上的高,
则点M与⊙C的关系如何? 例3 如图所示,在A地正北80m的B处有一幢民房,正西100m的C处有一变电设施,在BC的中点D处是一古建筑。 因施工需要,必须在A处进行一次爆破。为使民房、变电设施、古建筑都不遭到破坏,问爆破影响面的半径应控制在什么范围内?
解:连结AD·2cm3cm1.画出由所有到已知点的距离大于或等于2cm并且小于或等于3cm的点组成的图形.O练习练一练 1、⊙O的半径10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在 ;点B在 ;点C在 。 2、⊙O的半径6cm,当OP=6时,点p在 ;
当OP 时点P在圆内;当OP 时,点P不在圆外。 3、正方形ABCD的边长为2cm,以A为圆心,2cm为半径作⊙A,则点B在⊙A ;点C在⊙A ;点D在⊙A 。圆内圆上圆外圆上<6≤6 上外上 4、已知AB为⊙O的直径,P为⊙O 上任意一点,则点p关于AB的对称点P′与⊙O的位置为( )
(A)在⊙O内 (B)在⊙O 外 (C)在⊙O 上 (D)不能确定 c 这节课你学到了哪些知识?点与圆的位置关系: 设⊙O 的半径为r,点P到圆心的距离OP=d,则有:
注意:点与圆的位置关系和点到圆心的距离的数量关系是互相对应的,即知道位置关系可以确定数量关系,知道数量关系可以确定位置关系.点P在⊙O内 d<r 点P在⊙O上 d=r 点P在⊙O外 d>r 点的位置可以确定该点到圆心的距离与半径的关系,反过来,已知点到圆心的距离与半径的关系可以确定该点和圆的位置关系。
课本 P93 练习 1 ;
P101 习题 24.2 1再见24.2.1.2点和圆的位置关系(2)回顾:r·OAPPPd > rd < rd = r点P在圆外点P在圆内点P在圆上点与圆的位置关系●A●A●B过一点可作几条直线?过两点可以作几条直线?过三点呢?过两点有且只有一条直线(直线公理)
(“有且只有”就是“确定”的意思)
经过一点可以作无数条直线;
回忆思考:过三点直线公理:两点确定一条直线 对于一个圆来说,过几个点能作一个圆,并且只能作一个圆?类比探究: 1、平面上有一点A,经过已知A点的圆有几个?圆心在哪里? ●A 无数个,圆心为点A以外任意一点,半径为这点与点A的距离 2、平面上有两点A、B,经过已知点A、B的圆有几个?它们的圆心分布有什么特点? 以线段AB的垂直平分线上的任意一点为圆心,以这点到A或B的距离为半径作圆. 无数个。它们的圆心都在线段AB的垂直平分线上。 3、平面上有三点A、B、C,经过A、B、 C三点的圆有几个?圆心在哪里? 归纳结论:
不在同一条直线上的三个点确定一个圆。●B●C 经过B,C两点的圆的圆心在线段AB的垂直平分线上.●A 经过A,B,C三点的圆的圆心应该是这两条垂直平分线的交点O的位置.●O 经过A,B两点的圆的圆心在线段AB的垂直平分线上.1、连结AB,作线段AB的垂直平分线DE,2、连结BC,作线段BC的垂直平分线FG,交DE于点O,3、以O为圆心,OB为半径作圆,作法:⊙O就是所求作的圆已知:不在同一直线上的三点 A、B、C
求作:⊙O,使它经过A、B、C 三点不共线 请你证明你作的圆符合要求证明:∵点O在AB的垂直平分线上,
∴OA=OB.
同理,OB=OC.
∴OA=OB=OC.
∴点A,B,C在以O为圆心,OA长为半径的圆上.
∴⊙O就是所求作的圆,
在上面的作图过程中.
∵直线DE和FG只有一个交点O,并且点O到A,B,C三个点的距离相等,
∴经过点A,B,C三点可以作一个圆,并且只能作一个圆.
你能过三角形的三个顶点作圆吗?如何作?ABC 经过三角形三个顶点可以画一个圆,并且只能画一个.经过三角形三个顶点的圆叫做三角形的外接圆。三角形的外心就是三角形三条边的垂直平分线的交点,它到三角形三个顶点的距离相等。这个三角形叫做这个圆的内接三角形。三角形外接圆的圆心叫做这个三角形的外心。●O思考:一个三角形的外接圆有几个
一个圆的内接三角形有几个一个无数个圆的内接三角 形三角形的外接 圆三角形 的外心ABCO 分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系. 锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.1 图中△ABC外接圆的圆心坐标是________.经过同一条直线三个点能作出一个圆吗? 如图,假设过同一条直线l上三点A、B、C可以做一个圆,设这个圆的圆心为P,那么点P既在线段AB的垂直平分线l1上,又在线段BC的垂直平分线l2上,即点P为l1与l2的交点,而l1⊥l,l2⊥l这与我们以前学过的“过一点有且只有一条直线与已知直线垂直相矛盾,所以过同一条直线上的三点不能做圆. 上面的证明“过同一条直线上的三点不能做圆”的方法与我门以前学过的证明不同,它不是直接从命题的已知得结论,而是假设命题的结论不成立(即假设过同一条直线上的三点可以作一个圆),由此经过推理的出矛盾,由矛盾判定假设不正确,从而得到原命题成立,这种方法叫做反证法.p92页反证法应用例先假设命题的结论不成立,然后由此经过推理得出矛盾(常与公理、定理、定义或已知条件相矛盾),由矛盾判定假设不正确,从而得到原命题成立,这种方法叫做反证法.什么叫反证法? 任意四个点是不是可以画一个圆?请举例说明. 不一定 (1) 四点在一条直线上不能作圆; (3)四点中任意三点不在一条直线可能作圆也可能做不出一个圆.ABCDABCDABCDABCD (2)三点在同一直线上, 另一点不在这条直线上不能做圆; 1、判断下列说法是否正确
(1)任意的一个三角形一定有一个外接圆( ).
(2)任意一个圆有且只有一个内接三角形( )
(3)经过三点一定可以确定一个圆( )
(4)三角形的外心到三角形各顶点的距离相等( ) 2、若一个三角形的外心在一边上,则此三角形的 形状为( )
A、锐角三角形 B、直角三角形
C、钝角三角形 D、等腰三角形√××√B3: 如图,CD所在的直线垂直平分线段AB,怎样用这样的工具找到圆形工件的圆心.DO∵A、B两点在圆上,所以圆心必与A、B两点的距离相等,又∵和一条线段的两个端点距离相等的点在这条线段的垂直平分线上,∴圆心在CD所在的直线上,因此可以做任意两条直径,它们的交点为圆心.4、如图,AD是△ABC的外角∠EAC的平分线,AD与三角形的外接圆交于点D,连接BD,求证:DB=DC.5如图,△ABC中,AB=AC=10,BC=12,求△ABC的外接圆半径。解:过点A作AD⊥BC于D,由AB=AC知外接圆的圆心在AD上,记为O,故BD=1/2 BC=6,连接OB.设OA=OB=x.DO由BD2+OD2=OB2得,62+(8-x)2=x2解得即外接圆的半径为 .我学会了什么 ?小结:1.点与圆的位置关系2.不在同一条直线上的三个点确定一个圆。锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.点A在⊙O内 d<r d=r d>r点P在⊙O内点P在⊙O上点P在⊙O外3.三角形的外心就是三角形三条边的垂直平分线的交点,它到三角形三个顶点的距离相等。
设⊙O半径为r,说出点A,点B,点C与圆心O的距离与半径的关系:·COABOC > r.问题一:
观察图中点A,点B,点C与圆的位置关系?点C在圆外.点A在圆内,点B在圆上,OA < r,OB = r,探究新知设⊙O的半径为r,点P到圆心的距离OP = d,则有:r·OA问题三:
反过来,已知点到圆心的距离和圆的半径,能否判断点和圆的位置关系?PPP点A在⊙O内 d<r d=r d>r点B在⊙O上 点P在⊙O内点P在⊙O上点P在⊙O外 数量关系 位置关系 设⊙O 的半径为r,点P到圆心的距离OP=d,则有:点P在⊙O内 点P在⊙O上 点P在⊙O外 d<r d=r d>rd读作“等价于”,它表示从符号左端可以得到右端,也可以从右端得到左端。圆外的点圆内的点圆上的点 平面上的一个圆,把平面上的点分成三类:圆上的点,圆内的点和圆外的点。 圆的内部可以看成是到圆心的距离小于半径的点的集合;外部可以看成是 到圆心的距离大于半径的点的集合。思考:平面上的一个圆把平面上的点分成哪几部分? 射击靶图上,有一组以靶心为圆心的大小不同的圆,他们把靶图由内到外分成几个区域,这些区域用由高到底的环数来表示,射击成绩用弹着点位置对应的环数来表示.弹着点与靶心的距离决定了它在哪个圆内,弹着点离靶心越近,它所在的区域就越靠内,对应的环数也就越高,射击的成绩越好.你知道击中靶上不同位置的成绩是如何计算的吗 ?例1:如图已知矩形ABCD的边AB=3厘米,AD=4厘米 (1)以点A为圆心,3厘米为半径作圆A,则点B、C、D与圆A的位置关系如何? (B在圆上,D在圆外,C在圆外)(2)以点A为圆心,4厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?(B在圆内,D在圆上,C在圆外)(3)以点A为圆心,5厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?(B在圆内,D在圆内,C在圆上)若以A点为圆心作圆A,使B、C、D
三点中至少有一个点在圆内,且至少有一个
点在圆外,则圆A的半径r的取值范围是什么?例题2(1)若CM是AB边中线, 则点A、B、M与 ⊙C的关系如何?(2)若CM是AB边上的高,
则点M与⊙C的关系如何? 例3 如图所示,在A地正北80m的B处有一幢民房,正西100m的C处有一变电设施,在BC的中点D处是一古建筑。 因施工需要,必须在A处进行一次爆破。为使民房、变电设施、古建筑都不遭到破坏,问爆破影响面的半径应控制在什么范围内?
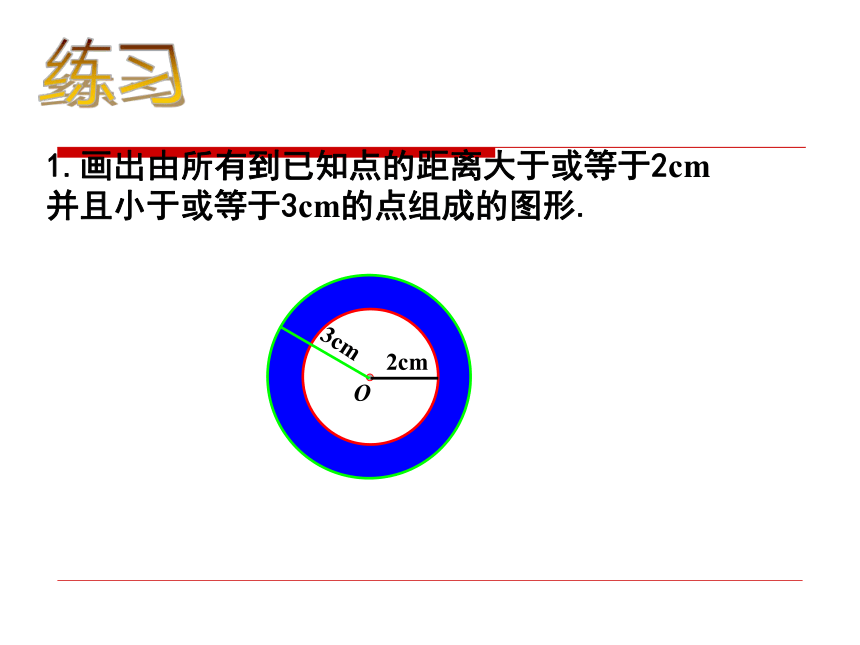
解:连结AD·2cm3cm1.画出由所有到已知点的距离大于或等于2cm并且小于或等于3cm的点组成的图形.O练习练一练 1、⊙O的半径10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在 ;点B在 ;点C在 。 2、⊙O的半径6cm,当OP=6时,点p在 ;
当OP 时点P在圆内;当OP 时,点P不在圆外。 3、正方形ABCD的边长为2cm,以A为圆心,2cm为半径作⊙A,则点B在⊙A ;点C在⊙A ;点D在⊙A 。圆内圆上圆外圆上<6≤6 上外上 4、已知AB为⊙O的直径,P为⊙O 上任意一点,则点p关于AB的对称点P′与⊙O的位置为( )
(A)在⊙O内 (B)在⊙O 外 (C)在⊙O 上 (D)不能确定 c 这节课你学到了哪些知识?点与圆的位置关系: 设⊙O 的半径为r,点P到圆心的距离OP=d,则有:
注意:点与圆的位置关系和点到圆心的距离的数量关系是互相对应的,即知道位置关系可以确定数量关系,知道数量关系可以确定位置关系.点P在⊙O内 d<r 点P在⊙O上 d=r 点P在⊙O外 d>r 点的位置可以确定该点到圆心的距离与半径的关系,反过来,已知点到圆心的距离与半径的关系可以确定该点和圆的位置关系。
课本 P93 练习 1 ;
P101 习题 24.2 1再见24.2.1.2点和圆的位置关系(2)回顾:r·OAPPPd > rd < rd = r点P在圆外点P在圆内点P在圆上点与圆的位置关系●A●A●B过一点可作几条直线?过两点可以作几条直线?过三点呢?过两点有且只有一条直线(直线公理)
(“有且只有”就是“确定”的意思)
经过一点可以作无数条直线;
回忆思考:过三点直线公理:两点确定一条直线 对于一个圆来说,过几个点能作一个圆,并且只能作一个圆?类比探究: 1、平面上有一点A,经过已知A点的圆有几个?圆心在哪里? ●A 无数个,圆心为点A以外任意一点,半径为这点与点A的距离 2、平面上有两点A、B,经过已知点A、B的圆有几个?它们的圆心分布有什么特点? 以线段AB的垂直平分线上的任意一点为圆心,以这点到A或B的距离为半径作圆. 无数个。它们的圆心都在线段AB的垂直平分线上。 3、平面上有三点A、B、C,经过A、B、 C三点的圆有几个?圆心在哪里? 归纳结论:
不在同一条直线上的三个点确定一个圆。●B●C 经过B,C两点的圆的圆心在线段AB的垂直平分线上.●A 经过A,B,C三点的圆的圆心应该是这两条垂直平分线的交点O的位置.●O 经过A,B两点的圆的圆心在线段AB的垂直平分线上.1、连结AB,作线段AB的垂直平分线DE,2、连结BC,作线段BC的垂直平分线FG,交DE于点O,3、以O为圆心,OB为半径作圆,作法:⊙O就是所求作的圆已知:不在同一直线上的三点 A、B、C
求作:⊙O,使它经过A、B、C 三点不共线 请你证明你作的圆符合要求证明:∵点O在AB的垂直平分线上,
∴OA=OB.
同理,OB=OC.
∴OA=OB=OC.
∴点A,B,C在以O为圆心,OA长为半径的圆上.
∴⊙O就是所求作的圆,
在上面的作图过程中.
∵直线DE和FG只有一个交点O,并且点O到A,B,C三个点的距离相等,
∴经过点A,B,C三点可以作一个圆,并且只能作一个圆.
你能过三角形的三个顶点作圆吗?如何作?ABC 经过三角形三个顶点可以画一个圆,并且只能画一个.经过三角形三个顶点的圆叫做三角形的外接圆。三角形的外心就是三角形三条边的垂直平分线的交点,它到三角形三个顶点的距离相等。这个三角形叫做这个圆的内接三角形。三角形外接圆的圆心叫做这个三角形的外心。●O思考:一个三角形的外接圆有几个
一个圆的内接三角形有几个一个无数个圆的内接三角 形三角形的外接 圆三角形 的外心ABCO 分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系. 锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.1 图中△ABC外接圆的圆心坐标是________.经过同一条直线三个点能作出一个圆吗? 如图,假设过同一条直线l上三点A、B、C可以做一个圆,设这个圆的圆心为P,那么点P既在线段AB的垂直平分线l1上,又在线段BC的垂直平分线l2上,即点P为l1与l2的交点,而l1⊥l,l2⊥l这与我们以前学过的“过一点有且只有一条直线与已知直线垂直相矛盾,所以过同一条直线上的三点不能做圆. 上面的证明“过同一条直线上的三点不能做圆”的方法与我门以前学过的证明不同,它不是直接从命题的已知得结论,而是假设命题的结论不成立(即假设过同一条直线上的三点可以作一个圆),由此经过推理的出矛盾,由矛盾判定假设不正确,从而得到原命题成立,这种方法叫做反证法.p92页反证法应用例先假设命题的结论不成立,然后由此经过推理得出矛盾(常与公理、定理、定义或已知条件相矛盾),由矛盾判定假设不正确,从而得到原命题成立,这种方法叫做反证法.什么叫反证法? 任意四个点是不是可以画一个圆?请举例说明. 不一定 (1) 四点在一条直线上不能作圆; (3)四点中任意三点不在一条直线可能作圆也可能做不出一个圆.ABCDABCDABCDABCD (2)三点在同一直线上, 另一点不在这条直线上不能做圆; 1、判断下列说法是否正确
(1)任意的一个三角形一定有一个外接圆( ).
(2)任意一个圆有且只有一个内接三角形( )
(3)经过三点一定可以确定一个圆( )
(4)三角形的外心到三角形各顶点的距离相等( ) 2、若一个三角形的外心在一边上,则此三角形的 形状为( )
A、锐角三角形 B、直角三角形
C、钝角三角形 D、等腰三角形√××√B3: 如图,CD所在的直线垂直平分线段AB,怎样用这样的工具找到圆形工件的圆心.DO∵A、B两点在圆上,所以圆心必与A、B两点的距离相等,又∵和一条线段的两个端点距离相等的点在这条线段的垂直平分线上,∴圆心在CD所在的直线上,因此可以做任意两条直径,它们的交点为圆心.4、如图,AD是△ABC的外角∠EAC的平分线,AD与三角形的外接圆交于点D,连接BD,求证:DB=DC.5如图,△ABC中,AB=AC=10,BC=12,求△ABC的外接圆半径。解:过点A作AD⊥BC于D,由AB=AC知外接圆的圆心在AD上,记为O,故BD=1/2 BC=6,连接OB.设OA=OB=x.DO由BD2+OD2=OB2得,62+(8-x)2=x2解得即外接圆的半径为 .我学会了什么 ?小结:1.点与圆的位置关系2.不在同一条直线上的三个点确定一个圆。锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.点A在⊙O内 d<r d=r d>r点P在⊙O内点P在⊙O上点P在⊙O外3.三角形的外心就是三角形三条边的垂直平分线的交点,它到三角形三个顶点的距离相等。
同课章节目录
