2021-2022学年冀教版八年级数学上册第13章全等三角形期末综合复习训练 (word版、含解析)
文档属性
| 名称 | 2021-2022学年冀教版八年级数学上册第13章全等三角形期末综合复习训练 (word版、含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 255.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 10:32:45 | ||
图片预览

文档简介
2021-2022学年冀教版八年级数学上册《第13章全等三角形》期末综合复习训练(附答案)
1.如图,若△ABC≌△DEF,则∠E等于( )
A.30° B.50° C.60° D.100°
2.三角形中,到三边距离相等的点是( )
A.三条高线的交点 B.三条中线的交点
C.三条角平分线的交点 D.三边垂直平分线的交点
3.如图:若△ABE≌△ACF,且AB=5,AE=2,则EC的长为( )
A.2 B.2.5 C.3 D.5
4.如图,在△ABC中,AB=AC,∠BAD=∠CAD,则下列结论:①△ABD≌△ACD,②∠B=∠C,③BD=CD,④AD⊥BC.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
5.若△ABC≌△DEF,∠A=∠D,∠C=∠F,且△ABC的周长为20,AB=5,BC=8,则DF长为( )
A.5 B.8 C.7 D.5或8
6.如图,∠ACB=∠DFE,BF=CE,那么需要补充一个直接条件 (写出一个即可),才能使△ABC≌△DEF.
7.如图,在△ABC中,AD=AE,BD=EC,∠ADB=∠AEC,∠BAD=25°,则∠CAE的度数为 °.
8.如图,在△ABC中,∠C=90°,AD是∠BAC的角平分线,若BC=5cm,BD=3cm,则点D到AB的距离为 .
9.如图,在△ABC中,∠B=60°,AD平分∠BAC交BC于D,若AB+BD=AC,那么∠C= 度.
10.如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是28cm2,AB=8cm,AC=6cm,则DE= cm.
11.如图,在Rt△ABC中,∠C=90°,D是AC上一点,DE⊥AB于E,且DE=DC.若∠A=20°,则∠DBC的度数为 .
12.尺规作图(请保留作图痕迹,不写作法).
(1)在图1中作∠AOB的平分线.
(2)在图2中画△ABC,使其两边为已知线段a、b,夹角为β.
13.如图,AC=BD,BC=AD,求证:△ABC≌△BAD.
14.如图,AB=CD,AE⊥BC,DF⊥BC,CE=BF.求证:AE=DF.
15.如图,A、D、F、B在同一直线上,AD=BF,AE=BC,且AE∥BC.求证:
(1)△AEF≌△BCD;
(2)EF∥CD.
16.如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.
(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
17.如图,Rt△ABC中,∠BAC=90°,AB=AC,分别过点B、C作过点A的垂线BC、CE,垂足分别为D、E,若BD=3,CE=2,求DE的长.
18.如图:已知BD=CD,BF⊥AC,CE⊥AB,求证:点D在∠BAC的平分线上.
19.如图,已知AD平分∠BAC,∠BAC+∠BDC=180°.
(1)若AC=CD,∠B=50°,求∠ADB;
(2)若∠C是钝角,求证:BD=CD.
20.如图,AD是△ABC的高,E是AC上一点,BE交AD于F,且有BD=AD,DF=DC,试说明BE⊥AC.
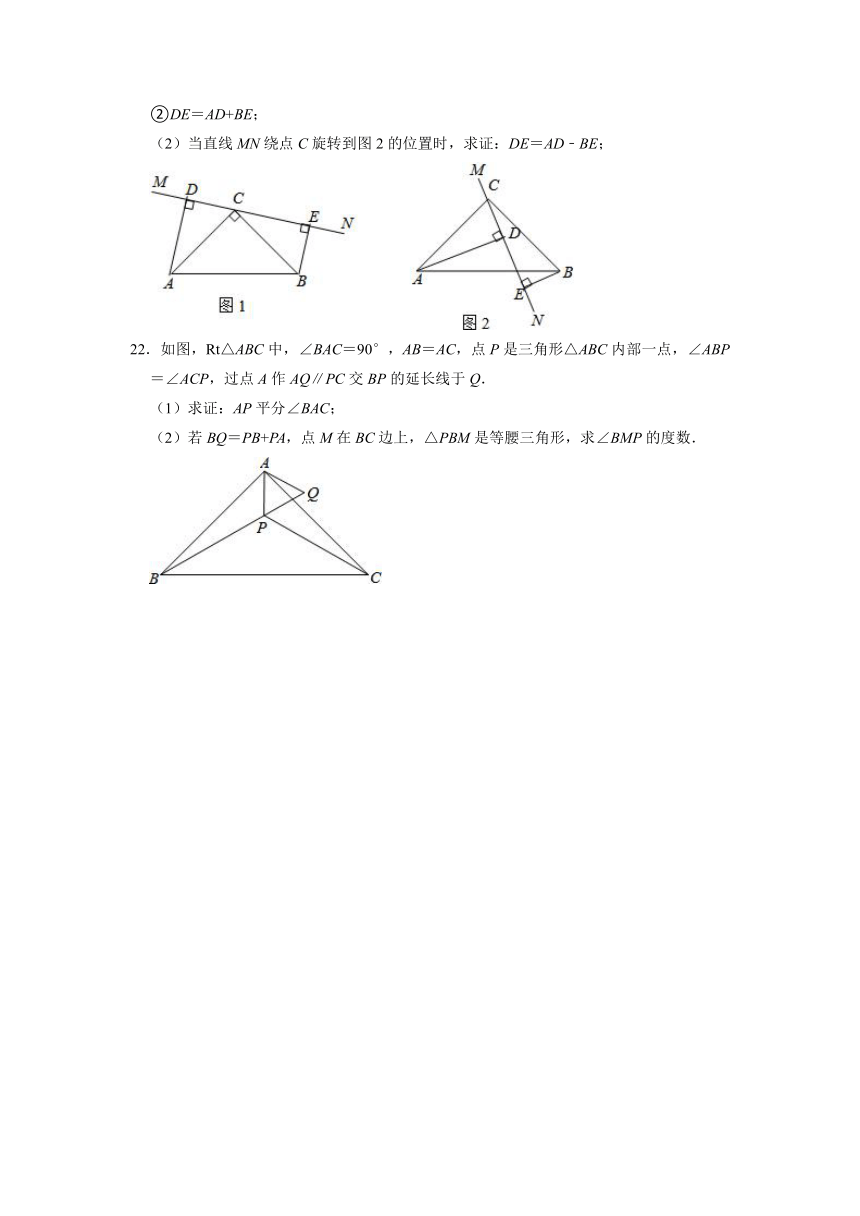
21.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:
①△ADC≌△CEB;
②DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD﹣BE;
22.如图,Rt△ABC中,∠BAC=90°,AB=AC,点P是三角形△ABC内部一点,∠ABP=∠ACP,过点A作AQ∥PC交BP的延长线于Q.
(1)求证:AP平分∠BAC;
(2)若BQ=PB+PA,点M在BC边上,△PBM是等腰三角形,求∠BMP的度数.
参考答案
1.解:∵△ABC≌△DEF,
∴∠E=∠B=180°﹣50°﹣30°=100°.
故选:D.
2.解:三角形中,到三边距离相等的点是三条角平分线的交点.
故选:C.
3.解:∵△ABE≌△ACF,AB=5,
∴AC=AB=5,
∵AE=2,
∴EC=AC﹣AE=5﹣2=3,
故选:C.
4.解:∵在△ABC中,AB=AC,∠BAD=∠CAD,
∴AD⊥BD,BD=CD,∠B=∠C,
∴△ABD≌△ACD(SSS).
故选:D.
5.解:如图:
∵△ABC的周长为20,AB=5,BC=8,
∴AC=20﹣5﹣8=7,
∵△ABC≌△DEF,∠A=∠D,∠C=∠F,
∴DF=AC=7.
故选:C.
6.解:补充的一个条件:AC=DF,
∵BF=CE,
∴BF﹣CF=CE﹣CF,
即:BC=EF,
在△ABC与△DEF中,
,
∴△ABC≌△DEF.
故答案为:AC=DF.
7.解:在△ABD与△ACE中,,
∴△ABD≌△ACE,
∴∠CAE=∠BAD,
∵∠BAD=25°,
∴∠CAE=25°,
故答案为:25.
8.解:过点D作DE⊥AB于E,
∵在△ABC中,∠C=90°,
∴DC⊥AC,
∵AD是∠BAC的角平分线,
∴DE=CD,
∵BC=5cm,BD=3cm,
∴CD=BC﹣BD=2cm,
∴DE=2cm.
∴点D到AB的距离为2cm.
故答案为:2cm.
9.解:如图,在AC上截取AE=AB,连接DE.
∵AD平分∠BAC,
∴∠BAD=∠EAD,
在△ABD与△ADE中,
,
∴△ABD≌△AED(SAS),
∴∠B=∠AED,DE=BD,
∵AB+BD=AC=AE+CE,
∴DE=CE,
∴∠EDC=∠C,
∵∠AED=∠C+∠EDC,
∴∠C=∠B﹣∠C,
∴∠C=∠B,
∵∠B=60°,
∴∠C=30°.
故答案为:30.
10.解:∵AD为∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DE=DF,
△ABC面积=×AB DE+×AC DF=28,
即×8DE+×6DE=28,
解得DE=4.
故答案为:4.
11.解:∵∠C=90°,∴DC⊥BC,∵DE⊥AB,DE=DC,
∴点D在∠ABC的平分线上,
∴BD平分∠ABC,
∵∠A=20°,
∴∠ABC=70°,
∵BD平分∠ABC,
∴∠DBC=∠ABD=35°,
故答案为:35°.
12.解:(1)如图1,OC为所作;
(2)如图2,△MNQ为所作.
13.证明:在△ABC与△BAD中,
,
∴△ABC≌△BAD(SSS).
14.证明:∵AE⊥BC,DF⊥BC,
∴∠DFC=∠AEB=90°,
又∵CE=BF,
∴CE﹣EF=BF﹣EF,即CF=BE,
∵AB=CD,
∴Rt△DFC≌Rt△AEB(HL),
∴AE=DF.
15.证明:(1)∵AE∥BC,
∴∠A=∠B.
又∵AD=BF,
∴AF=AD+DF=BF+FD=BD.
又∵AE=BC,
在△AEF和△BCD中,
,
∴△AEF≌△BCD(SAS).
(2)∵△AEF≌△BCD,
∴∠EFA=∠CDB.
∴EF∥CD.
16.(1)证明:∵BE=CF,
∴BE+EF=CF+EF,
即BF=CE.
又∵∠A=∠D,∠B=∠C,
∴△ABF≌△DCE(AAS),
∴AB=DC.
(2)解:△OEF为等腰三角形
理由如下:∵△ABF≌△DCE,
∴∠AFB=∠DEC,
∴OE=OF,
∴△OEF为等腰三角形.
17.解:∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵BD⊥DE,
∴∠BDA=90°,
∴∠BAD+∠DBA=90°,
∴∠DBA=∠CAE,
∵CE⊥DE,
∴∠E=90°,
在△BDA和△AEC中,
,
∴△BDA≌△AEC(AAS),
∴DA=CE=2,AE=DB=3,
∴ED=5.
18.证明:∵BF⊥AC,CE⊥AB,
∴∠BED=∠CFD=90°,
在△BED和△CFD中,
,
∴△BED≌△CFD(AAS),
∴DE=DF,
又∵DE⊥AB,DF⊥AC,
∴点D在∠BAC的平分线上.
19.解:(1)∵∠BAC+∠BDC=180°,
∴∠B+∠C=180°,
∵∠B=50°,
∴∠C=130°,
∵AC=CD,∠C=130°,
∴∠DAC=∠ADC=(180°﹣∠C)÷2=25°,
∵AD平分∠BAC,
∴∠BAC=2∠DAC=50°,
∵∠BAC+∠BDC=180°,
∴∠BDC=130°,
∴∠ADB=∠BDC﹣∠ADC=130°﹣25°=105°.
(2)如图,过点D作DM⊥AB于M,DN⊥AC交AC延长线于N,
∵AD平分∠BAC,DM⊥AB,DN⊥AC,
∴DM=DN,∠DMB=∠DNC=90,
∵∠ACD+∠B=180,∠ACD+∠DCN=180,
∴∠B=∠DCN,
在△BDM与△CDN中,
,
∴△DMB≌△DNC (AAS),
∴BD=CD.
20.证明:(1)∵AD为BC边上的高,
∴∠ADB=∠ADC=90°,
∵在△BDF和△ADC中,
,
∴△BDF≌△ADC(SAS),
∴∠EBC=∠CAD,
∵∠ADC=90°,
∴∠ACD+∠DAC=90°,
∴∠ACD+∠DBF=90°,
∴∠BEC=90°,
∴BE⊥AC.
21.(1)①证明:∵AD⊥DE,BE⊥DE,
∴∠ADC=∠BEC=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,
∴∠DAC=∠BCE,
在△ADC和△CEB中
,
∴△ADC≌△CEB(AAS).
②证明:由(1)知:△ADC≌△CEB,
∴AD=CE,CD=BE,
∵DC+CE=DE,
∴AD+BE=DE.
(2)证明:∵BE⊥EC,AD⊥CE,
∴∠ADC=∠BEC=90°,
∴∠EBC+∠ECB=90°,
∵∠ACB=90°,
∴∠ECB+∠ACE=90°,
∴∠ACD=∠EBC,
在△ADC和△CEB中
,
∴△ADC≌△CEB(AAS),
∴AD=CE,CD=BE,
∴DE=EC﹣CD=AD﹣BE.
22.(1)证明:∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∵∠ABP=∠ACP,
∴∠PBC=∠PCB,
∴PB=PC,
在△ABP和△ACP中
,
∴△ABP≌△ACP,
∴∠BAP=∠CAP,
∴AP平分∠BAC;
(2)∵BQ=PB+PA,
而BQ=BP+PQ,
∴PA=PQ,
∴∠PQA=∠PAQ=∠PAC+∠2,
∵AQ∥PC,
∴∠1=∠2,
设∠1=∠3=x,则∠PQA=∠PAQ=45°+x,
∴∠APQ=180°﹣2(45°+x)=x+45°,解得x=15°,
∴∠PBC=30°,
当MP=MB时,∠BMP=180°﹣2×30°=120°;
当PM=PB时,∠BMP=30°;
当BM=BP时,∠BMP=(180°﹣30°)=75°.
1.如图,若△ABC≌△DEF,则∠E等于( )
A.30° B.50° C.60° D.100°
2.三角形中,到三边距离相等的点是( )
A.三条高线的交点 B.三条中线的交点
C.三条角平分线的交点 D.三边垂直平分线的交点
3.如图:若△ABE≌△ACF,且AB=5,AE=2,则EC的长为( )
A.2 B.2.5 C.3 D.5
4.如图,在△ABC中,AB=AC,∠BAD=∠CAD,则下列结论:①△ABD≌△ACD,②∠B=∠C,③BD=CD,④AD⊥BC.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
5.若△ABC≌△DEF,∠A=∠D,∠C=∠F,且△ABC的周长为20,AB=5,BC=8,则DF长为( )
A.5 B.8 C.7 D.5或8
6.如图,∠ACB=∠DFE,BF=CE,那么需要补充一个直接条件 (写出一个即可),才能使△ABC≌△DEF.
7.如图,在△ABC中,AD=AE,BD=EC,∠ADB=∠AEC,∠BAD=25°,则∠CAE的度数为 °.
8.如图,在△ABC中,∠C=90°,AD是∠BAC的角平分线,若BC=5cm,BD=3cm,则点D到AB的距离为 .
9.如图,在△ABC中,∠B=60°,AD平分∠BAC交BC于D,若AB+BD=AC,那么∠C= 度.
10.如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是28cm2,AB=8cm,AC=6cm,则DE= cm.
11.如图,在Rt△ABC中,∠C=90°,D是AC上一点,DE⊥AB于E,且DE=DC.若∠A=20°,则∠DBC的度数为 .
12.尺规作图(请保留作图痕迹,不写作法).
(1)在图1中作∠AOB的平分线.
(2)在图2中画△ABC,使其两边为已知线段a、b,夹角为β.
13.如图,AC=BD,BC=AD,求证:△ABC≌△BAD.
14.如图,AB=CD,AE⊥BC,DF⊥BC,CE=BF.求证:AE=DF.
15.如图,A、D、F、B在同一直线上,AD=BF,AE=BC,且AE∥BC.求证:
(1)△AEF≌△BCD;
(2)EF∥CD.
16.如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.
(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
17.如图,Rt△ABC中,∠BAC=90°,AB=AC,分别过点B、C作过点A的垂线BC、CE,垂足分别为D、E,若BD=3,CE=2,求DE的长.
18.如图:已知BD=CD,BF⊥AC,CE⊥AB,求证:点D在∠BAC的平分线上.
19.如图,已知AD平分∠BAC,∠BAC+∠BDC=180°.
(1)若AC=CD,∠B=50°,求∠ADB;
(2)若∠C是钝角,求证:BD=CD.
20.如图,AD是△ABC的高,E是AC上一点,BE交AD于F,且有BD=AD,DF=DC,试说明BE⊥AC.
21.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:
①△ADC≌△CEB;
②DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD﹣BE;
22.如图,Rt△ABC中,∠BAC=90°,AB=AC,点P是三角形△ABC内部一点,∠ABP=∠ACP,过点A作AQ∥PC交BP的延长线于Q.
(1)求证:AP平分∠BAC;
(2)若BQ=PB+PA,点M在BC边上,△PBM是等腰三角形,求∠BMP的度数.
参考答案
1.解:∵△ABC≌△DEF,
∴∠E=∠B=180°﹣50°﹣30°=100°.
故选:D.
2.解:三角形中,到三边距离相等的点是三条角平分线的交点.
故选:C.
3.解:∵△ABE≌△ACF,AB=5,
∴AC=AB=5,
∵AE=2,
∴EC=AC﹣AE=5﹣2=3,
故选:C.
4.解:∵在△ABC中,AB=AC,∠BAD=∠CAD,
∴AD⊥BD,BD=CD,∠B=∠C,
∴△ABD≌△ACD(SSS).
故选:D.
5.解:如图:
∵△ABC的周长为20,AB=5,BC=8,
∴AC=20﹣5﹣8=7,
∵△ABC≌△DEF,∠A=∠D,∠C=∠F,
∴DF=AC=7.
故选:C.
6.解:补充的一个条件:AC=DF,
∵BF=CE,
∴BF﹣CF=CE﹣CF,
即:BC=EF,
在△ABC与△DEF中,
,
∴△ABC≌△DEF.
故答案为:AC=DF.
7.解:在△ABD与△ACE中,,
∴△ABD≌△ACE,
∴∠CAE=∠BAD,
∵∠BAD=25°,
∴∠CAE=25°,
故答案为:25.
8.解:过点D作DE⊥AB于E,
∵在△ABC中,∠C=90°,
∴DC⊥AC,
∵AD是∠BAC的角平分线,
∴DE=CD,
∵BC=5cm,BD=3cm,
∴CD=BC﹣BD=2cm,
∴DE=2cm.
∴点D到AB的距离为2cm.
故答案为:2cm.
9.解:如图,在AC上截取AE=AB,连接DE.
∵AD平分∠BAC,
∴∠BAD=∠EAD,
在△ABD与△ADE中,
,
∴△ABD≌△AED(SAS),
∴∠B=∠AED,DE=BD,
∵AB+BD=AC=AE+CE,
∴DE=CE,
∴∠EDC=∠C,
∵∠AED=∠C+∠EDC,
∴∠C=∠B﹣∠C,
∴∠C=∠B,
∵∠B=60°,
∴∠C=30°.
故答案为:30.
10.解:∵AD为∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DE=DF,
△ABC面积=×AB DE+×AC DF=28,
即×8DE+×6DE=28,
解得DE=4.
故答案为:4.
11.解:∵∠C=90°,∴DC⊥BC,∵DE⊥AB,DE=DC,
∴点D在∠ABC的平分线上,
∴BD平分∠ABC,
∵∠A=20°,
∴∠ABC=70°,
∵BD平分∠ABC,
∴∠DBC=∠ABD=35°,
故答案为:35°.
12.解:(1)如图1,OC为所作;
(2)如图2,△MNQ为所作.
13.证明:在△ABC与△BAD中,
,
∴△ABC≌△BAD(SSS).
14.证明:∵AE⊥BC,DF⊥BC,
∴∠DFC=∠AEB=90°,
又∵CE=BF,
∴CE﹣EF=BF﹣EF,即CF=BE,
∵AB=CD,
∴Rt△DFC≌Rt△AEB(HL),
∴AE=DF.
15.证明:(1)∵AE∥BC,
∴∠A=∠B.
又∵AD=BF,
∴AF=AD+DF=BF+FD=BD.
又∵AE=BC,
在△AEF和△BCD中,
,
∴△AEF≌△BCD(SAS).
(2)∵△AEF≌△BCD,
∴∠EFA=∠CDB.
∴EF∥CD.
16.(1)证明:∵BE=CF,
∴BE+EF=CF+EF,
即BF=CE.
又∵∠A=∠D,∠B=∠C,
∴△ABF≌△DCE(AAS),
∴AB=DC.
(2)解:△OEF为等腰三角形
理由如下:∵△ABF≌△DCE,
∴∠AFB=∠DEC,
∴OE=OF,
∴△OEF为等腰三角形.
17.解:∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵BD⊥DE,
∴∠BDA=90°,
∴∠BAD+∠DBA=90°,
∴∠DBA=∠CAE,
∵CE⊥DE,
∴∠E=90°,
在△BDA和△AEC中,
,
∴△BDA≌△AEC(AAS),
∴DA=CE=2,AE=DB=3,
∴ED=5.
18.证明:∵BF⊥AC,CE⊥AB,
∴∠BED=∠CFD=90°,
在△BED和△CFD中,
,
∴△BED≌△CFD(AAS),
∴DE=DF,
又∵DE⊥AB,DF⊥AC,
∴点D在∠BAC的平分线上.
19.解:(1)∵∠BAC+∠BDC=180°,
∴∠B+∠C=180°,
∵∠B=50°,
∴∠C=130°,
∵AC=CD,∠C=130°,
∴∠DAC=∠ADC=(180°﹣∠C)÷2=25°,
∵AD平分∠BAC,
∴∠BAC=2∠DAC=50°,
∵∠BAC+∠BDC=180°,
∴∠BDC=130°,
∴∠ADB=∠BDC﹣∠ADC=130°﹣25°=105°.
(2)如图,过点D作DM⊥AB于M,DN⊥AC交AC延长线于N,
∵AD平分∠BAC,DM⊥AB,DN⊥AC,
∴DM=DN,∠DMB=∠DNC=90,
∵∠ACD+∠B=180,∠ACD+∠DCN=180,
∴∠B=∠DCN,
在△BDM与△CDN中,
,
∴△DMB≌△DNC (AAS),
∴BD=CD.
20.证明:(1)∵AD为BC边上的高,
∴∠ADB=∠ADC=90°,
∵在△BDF和△ADC中,
,
∴△BDF≌△ADC(SAS),
∴∠EBC=∠CAD,
∵∠ADC=90°,
∴∠ACD+∠DAC=90°,
∴∠ACD+∠DBF=90°,
∴∠BEC=90°,
∴BE⊥AC.
21.(1)①证明:∵AD⊥DE,BE⊥DE,
∴∠ADC=∠BEC=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,
∴∠DAC=∠BCE,
在△ADC和△CEB中
,
∴△ADC≌△CEB(AAS).
②证明:由(1)知:△ADC≌△CEB,
∴AD=CE,CD=BE,
∵DC+CE=DE,
∴AD+BE=DE.
(2)证明:∵BE⊥EC,AD⊥CE,
∴∠ADC=∠BEC=90°,
∴∠EBC+∠ECB=90°,
∵∠ACB=90°,
∴∠ECB+∠ACE=90°,
∴∠ACD=∠EBC,
在△ADC和△CEB中
,
∴△ADC≌△CEB(AAS),
∴AD=CE,CD=BE,
∴DE=EC﹣CD=AD﹣BE.
22.(1)证明:∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∵∠ABP=∠ACP,
∴∠PBC=∠PCB,
∴PB=PC,
在△ABP和△ACP中
,
∴△ABP≌△ACP,
∴∠BAP=∠CAP,
∴AP平分∠BAC;
(2)∵BQ=PB+PA,
而BQ=BP+PQ,
∴PA=PQ,
∴∠PQA=∠PAQ=∠PAC+∠2,
∵AQ∥PC,
∴∠1=∠2,
设∠1=∠3=x,则∠PQA=∠PAQ=45°+x,
∴∠APQ=180°﹣2(45°+x)=x+45°,解得x=15°,
∴∠PBC=30°,
当MP=MB时,∠BMP=180°﹣2×30°=120°;
当PM=PB时,∠BMP=30°;
当BM=BP时,∠BMP=(180°﹣30°)=75°.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
