2021-2022学年华东师大版八年级数学下册第18章 平行四边形 测试题(Word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版八年级数学下册第18章 平行四边形 测试题(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 144.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 00:00:00 | ||
图片预览



文档简介
第18章 平行四边形
一、选择题(每小题4分,共28分)
1.已知在 ABCD中,∠A+∠C=240°,则∠B的度数是 ( )
A.100° B.60° C.80° D.160°
2.如图1,AB和CD是夹在两平行线l1,l2之间的平行线段.若AB=3,AC=2,则CD的长为 ( )
图1
A.3 B.2.5
C.2 D.以上都不对
3.如图2,在四边形ABCD中,对角线AC和BD相交于点O.下列条件不能判定四边形ABCD是平行四边形的是 ( )
图2
A.AB∥DC,AD∥BC
B.AB=DC,AD=BC
C.AB∥DC,AD=BC
D.OA=OC,OB=OD
4.如图3, ABCD的对角线交于点O,且AB=7,△OCD的周长为23,则 ABCD的两条对角线长的和是 ( )
图3
A.32 B.28 C.16 D.46
5.如图4,在△MBN中,BM=6,点A,C,D分别在MB,NB,MN上,四边形ABCD为平行四边形,∠NDC=∠MDA,那么 ABCD的周长是 ( )
图4
A.24 B.18
C.16 D.12
6.如图5, ABCD的对角线AC,BD相交于点O,AB=12,AC=10,BD=26,则 ABCD的面积为 ( )
图5
A.100 B.110
C.120 D.130
7.如图6所示,在四边形ABCD中,AB=CD,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连结AF,CE.若DE=BF,有下列结论:①CF=AE;②OE=OF;③四边形ABCD是平行四边形;④图中共有四对全等三角形.其中正确结论的个数是 ( )
图6
A.4 B.3 C.2 D.1
二、填空题(每小题4分,共20分)
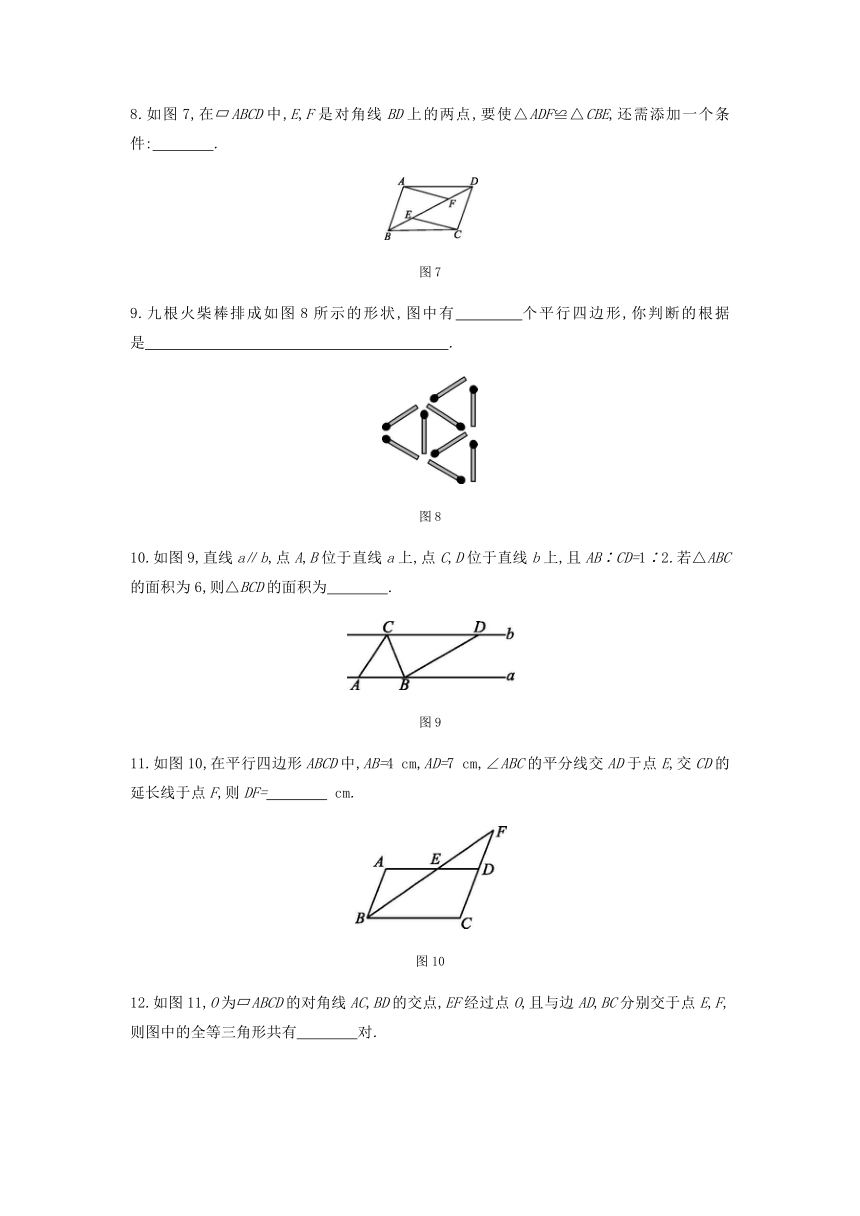
8.如图7,在 ABCD中,E,F是对角线BD上的两点,要使△ADF≌△CBE,还需添加一个条件: .
图7
9.九根火柴棒排成如图8所示的形状,图中有 个平行四边形,你判断的根据是 .
图8
10.如图9,直线a∥b,点A,B位于直线a上,点C,D位于直线b上,且AB∶CD=1∶2.若△ABC的面积为6,则△BCD的面积为 .
图9
11.如图10,在平行四边形ABCD中,AB=4 cm,AD=7 cm,∠ABC的平分线交AD于点E,交CD的延长线于点F,则DF= cm.
图10
12.如图11,O为 ABCD的对角线AC,BD的交点,EF经过点O,且与边AD,BC分别交于点E,F,则图中的全等三角形共有 对.
图11
三、解答题(共52分)
13.(10分)如图12,在 ABCD中,E,F分别是AB,DC的中点.
求证:∠DEA=∠BFC.
图12
14.(12分)如图13,在 ABCD中,在BC上取一点E,使得DE=AD,在DE上取一点F,使得∠AFE=∠ADC.
求证:(1)∠AFD=∠C;
(2)DF=CE.
图13
15.(14分)如图14,在四边形ABCD中,AB∥CD,BC⊥CD,E是AD的中点,连结BE并延长交CD的延长线于点F.
(1)连结AF,BD,试判断四边形ABDF是何种特殊四边形,并说明理由;
(2)若AB=4,BC=5,CD=6,求△BCF的面积.
图14
16.(16分)如图15,在平行四边形ABCD中,∠DAB=60°,点E,F分别在CD,AB的延长线上,且AE=AD,CF=CB.
(1)求证:四边形AFCE是平行四边形.
(2)若去掉已知条件“∠DAB=60”,上述结论还成立吗 若成立,请写出证明过程;若不成立,请说明理由.
图15
答案
1.B 2.A 3.C 4.A 5.D 6.C 7.B
8.答案不唯一,如BE=DF或BF=DE或∠BCE=∠DAF或AF∥EC等
9.3 两组对边分别相等的四边形是平行四边形
10.12
11.3
12.6
14.证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠C+∠ADC=180°.
∵∠AFD+∠AFE=180°,∠AFE=∠ADC,
∴∠AFD=∠C.
(2)∵AD∥BC,∴∠ADF=∠DEC.
在△AFD和△DCE中,
∵∠ADF=∠DEC,∠AFD=∠C,AD=DE,
∴△AFD≌△DCE(A.A.S.),
∴DF=CE.
15.解:(1)四边形ABDF是平行四边形.理由如下:
∵AB∥CD,∴∠BAE=∠FDE.
∵E是AD的中点,∴AE=DE.
在△ABE和△DFE中,
∵∠BAE=∠FDE,AE=DE,∠AEB=∠DEF,
∴△ABE≌△DFE,∴BE=FE.
又∵AE=DE,
∴四边形ABDF是平行四边形.
(2)由(1)知△ABE≌△DFE,
∴△BCF的面积=梯形ABCD的面积=
(AB+CD)·BC=×(4+6)×5=25.
16.解:(1)证明:∵四边形ABCD是平行四边形,
∴DC∥AB,∠DCB=∠DAB=60°,
∴∠ADE=∠DAB=60°,∠CBF=∠DCB=60°.
又∵AE=AD,CF=CB,
∴△AED,△CFB都是等边三角形,
∴∠AEC=∠BFC=60°,
∴∠EAF=∠FCE=120°,
∴∠BFC+∠EAF=180°,
∴AE∥CF.
又∵AF∥CE,
∴四边形AFCE是平行四边形.
(2)上述结论仍成立.
证明:∵四边形ABCD是平行四边形,
∴AD=BC,AB∥CD,∠ADC=∠ABC.
∵∠ADC+∠ADE=∠ABC+∠CBF=180°,
∴∠ADE=∠CBF.
∵AD=AE,CF=CB,
∴∠ADE=∠AED,∠CBF=∠CFB,
∴∠AED=∠CFB.
∵AF∥CE,
∴∠AED+∠EAF=180°,
∴∠CFB+∠EAF=180°,
∴AE∥CF.
又∵AF∥CE,
∴四边形AFCE是平行四边形.
一、选择题(每小题4分,共28分)
1.已知在 ABCD中,∠A+∠C=240°,则∠B的度数是 ( )
A.100° B.60° C.80° D.160°
2.如图1,AB和CD是夹在两平行线l1,l2之间的平行线段.若AB=3,AC=2,则CD的长为 ( )
图1
A.3 B.2.5
C.2 D.以上都不对
3.如图2,在四边形ABCD中,对角线AC和BD相交于点O.下列条件不能判定四边形ABCD是平行四边形的是 ( )
图2
A.AB∥DC,AD∥BC
B.AB=DC,AD=BC
C.AB∥DC,AD=BC
D.OA=OC,OB=OD
4.如图3, ABCD的对角线交于点O,且AB=7,△OCD的周长为23,则 ABCD的两条对角线长的和是 ( )
图3
A.32 B.28 C.16 D.46
5.如图4,在△MBN中,BM=6,点A,C,D分别在MB,NB,MN上,四边形ABCD为平行四边形,∠NDC=∠MDA,那么 ABCD的周长是 ( )
图4
A.24 B.18
C.16 D.12
6.如图5, ABCD的对角线AC,BD相交于点O,AB=12,AC=10,BD=26,则 ABCD的面积为 ( )
图5
A.100 B.110
C.120 D.130
7.如图6所示,在四边形ABCD中,AB=CD,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连结AF,CE.若DE=BF,有下列结论:①CF=AE;②OE=OF;③四边形ABCD是平行四边形;④图中共有四对全等三角形.其中正确结论的个数是 ( )
图6
A.4 B.3 C.2 D.1
二、填空题(每小题4分,共20分)
8.如图7,在 ABCD中,E,F是对角线BD上的两点,要使△ADF≌△CBE,还需添加一个条件: .
图7
9.九根火柴棒排成如图8所示的形状,图中有 个平行四边形,你判断的根据是 .
图8
10.如图9,直线a∥b,点A,B位于直线a上,点C,D位于直线b上,且AB∶CD=1∶2.若△ABC的面积为6,则△BCD的面积为 .
图9
11.如图10,在平行四边形ABCD中,AB=4 cm,AD=7 cm,∠ABC的平分线交AD于点E,交CD的延长线于点F,则DF= cm.
图10
12.如图11,O为 ABCD的对角线AC,BD的交点,EF经过点O,且与边AD,BC分别交于点E,F,则图中的全等三角形共有 对.
图11
三、解答题(共52分)
13.(10分)如图12,在 ABCD中,E,F分别是AB,DC的中点.
求证:∠DEA=∠BFC.
图12
14.(12分)如图13,在 ABCD中,在BC上取一点E,使得DE=AD,在DE上取一点F,使得∠AFE=∠ADC.
求证:(1)∠AFD=∠C;
(2)DF=CE.
图13
15.(14分)如图14,在四边形ABCD中,AB∥CD,BC⊥CD,E是AD的中点,连结BE并延长交CD的延长线于点F.
(1)连结AF,BD,试判断四边形ABDF是何种特殊四边形,并说明理由;
(2)若AB=4,BC=5,CD=6,求△BCF的面积.
图14
16.(16分)如图15,在平行四边形ABCD中,∠DAB=60°,点E,F分别在CD,AB的延长线上,且AE=AD,CF=CB.
(1)求证:四边形AFCE是平行四边形.
(2)若去掉已知条件“∠DAB=60”,上述结论还成立吗 若成立,请写出证明过程;若不成立,请说明理由.
图15
答案
1.B 2.A 3.C 4.A 5.D 6.C 7.B
8.答案不唯一,如BE=DF或BF=DE或∠BCE=∠DAF或AF∥EC等
9.3 两组对边分别相等的四边形是平行四边形
10.12
11.3
12.6
14.证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠C+∠ADC=180°.
∵∠AFD+∠AFE=180°,∠AFE=∠ADC,
∴∠AFD=∠C.
(2)∵AD∥BC,∴∠ADF=∠DEC.
在△AFD和△DCE中,
∵∠ADF=∠DEC,∠AFD=∠C,AD=DE,
∴△AFD≌△DCE(A.A.S.),
∴DF=CE.
15.解:(1)四边形ABDF是平行四边形.理由如下:
∵AB∥CD,∴∠BAE=∠FDE.
∵E是AD的中点,∴AE=DE.
在△ABE和△DFE中,
∵∠BAE=∠FDE,AE=DE,∠AEB=∠DEF,
∴△ABE≌△DFE,∴BE=FE.
又∵AE=DE,
∴四边形ABDF是平行四边形.
(2)由(1)知△ABE≌△DFE,
∴△BCF的面积=梯形ABCD的面积=
(AB+CD)·BC=×(4+6)×5=25.
16.解:(1)证明:∵四边形ABCD是平行四边形,
∴DC∥AB,∠DCB=∠DAB=60°,
∴∠ADE=∠DAB=60°,∠CBF=∠DCB=60°.
又∵AE=AD,CF=CB,
∴△AED,△CFB都是等边三角形,
∴∠AEC=∠BFC=60°,
∴∠EAF=∠FCE=120°,
∴∠BFC+∠EAF=180°,
∴AE∥CF.
又∵AF∥CE,
∴四边形AFCE是平行四边形.
(2)上述结论仍成立.
证明:∵四边形ABCD是平行四边形,
∴AD=BC,AB∥CD,∠ADC=∠ABC.
∵∠ADC+∠ADE=∠ABC+∠CBF=180°,
∴∠ADE=∠CBF.
∵AD=AE,CF=CB,
∴∠ADE=∠AED,∠CBF=∠CFB,
∴∠AED=∠CFB.
∵AF∥CE,
∴∠AED+∠EAF=180°,
∴∠CFB+∠EAF=180°,
∴AE∥CF.
又∵AF∥CE,
∴四边形AFCE是平行四边形.
