华东师大版数学八年级上册 第14章 勾股定理的复习课 课件(共12张PPT)
文档属性
| 名称 | 华东师大版数学八年级上册 第14章 勾股定理的复习课 课件(共12张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 19:09:32 | ||
图片预览




文档简介
(共12张PPT)
华东师大版 数学 八年级上册
勾股定理(毕达哥拉斯定理)
如果直角三角形两直角边分别为a、b 斜边为c,那么
a
c
b
A
C
B
即直角三角形两直角边的平方和等于斜边的平方。
结论变形
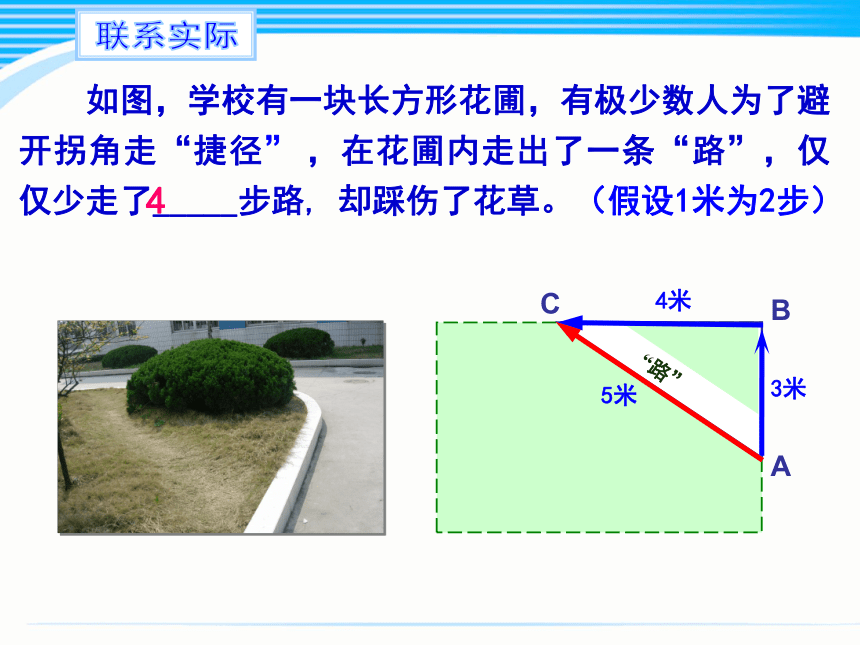
如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径” ,在花圃内走出了一条“路”,仅仅少走了_____步路, 却踩伤了花草。(假设1米为2步)
“路”
3米
4米
A
B
C
4
5米
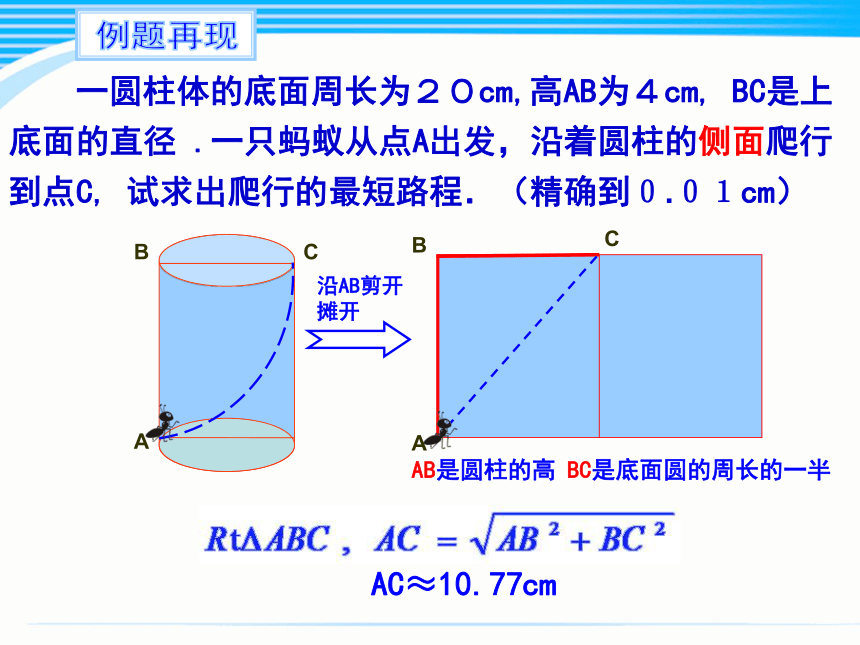
一圆柱体的底面周长为20cm,高AB为4cm, BC是上底面的直径 .一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C, 试求出爬行的最短路程.(精确到0.01cm)
沿AB剪开摊开
A
C
B
C
B
A
BC是底面圆的周长的一半
AB是圆柱的高
AC≈10.77cm
如图(1),一圆柱的底面半径为5,BC是底面直径,圆柱高AB为5,求一只蚂蚁从点A出发沿圆柱表面爬行到点C的最短路线。
小明设计了两条路线:
路线1:侧面展开图中的线段AC.如图(2)所示. 用L1表示
设路线1的长度为L1 ,则L12= AC2 =AB2+BC2 =52+(5π)2 =25+25π2
路线2:高线AB+底面直径BC.如图(1)所示.用L2表示
设路线2的长度为L2,则L22 = (AB+BC)2 =(5+10)2=225
∵ L12-L22=25+25π2-225=25(π2-8)>0
∴ L12>L22. ∴ L1>L2
所以选择路线L2较短.
小明对上述结论有些疑惑,于是他把条件改成:“圆柱的底面半径为1,高AB为10”继续按前面的路线进行计算.请你帮小明完成下面的计算:
路线1:L12=AC2= .
路线2:L22=(AB+BC)2 = . ∵ L12 L22, ∴ L1 L2 (填“<”或者 “>”) 所以选择路线 (填L1或L2)较短.
AB2+BC2=102+π2=100+π2
(10+2)2=144
<
<
L1
图①
图②
请你帮小明继续研究:在一般情况下,当圆柱的底面半径为r和高为h满足什么条件时,应如何选择上面的两条路线才能使蚂蚁从点A出发沿圆柱表面爬行到点C的路线最短.(分组讨论,看哪组最快得到答案)
图①
图②
L1=AC
L2=AB+BC
解法如下:
L12=AC2=
AB2+BC2=
h2+(πr)2
L22=(AB+BC)2=
(h+2r)2
L12-L22=h2+(πr)2 -(h+2r)2=r(π2r-4r-4h)=r[(π2-4)r-4h ]
∵L1 >0,L2 >0
∴L1和L2的大小,与L12 和L22的大小关系一样,
又∵r>0, π2-4>0
∴当r= 时,L12 = L22 ,L1= L2,选择路线L1, L2都一样;
当r> 时,L12 >L22 ,L1> L2,选择路线L2较短;
当r< 时,L12< L22 ,L1< L2 ,选择路线L1较短。
图①所示的正方体木块棱长为6cm,沿其相邻三个面的对角线(图中虚线)剪掉一角,得到如图②的几何体,一只蚂蚁沿着图②的几何体表面从顶点A爬行到顶点B的最短距离为 cm.
A(基础练习):
3( + )
c
如图长为3cm,宽为2cm,高为1cm的长方体,蚂蚁沿着表面从点A到点B需要爬行的最短路程是多少?
B( 提高练习):
B
A
1
3
2
前面与上面
AB=
AB=
AB=
B
A
3
2
前面与右侧
1
A
B
下面与右侧
A
B
2
1
3
本节课主要学习了勾股定理的应用——立体图形中最短路径问题,其一般解题思路如下:
1、展:立体图形 → 平面图形;
2、找:最短路线 起点→终点 依据是平面内两点之间线段最短;
3、算:构造出直角三角形,从而利用勾股定理进行计算。
本节课你有什么收获或感想?你还有什么疑问?
基础题:如图是一个三级台阶,它的每一级的长、宽、高分别为20dm、3dm、2dm,点A、点B是这个台阶两个相对的端点,点A有一只蚂蚁,想到点B去吃可口的食物,则蚂蚁沿着台阶面爬到点B最短路程是多少?
中等题:如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3 cm的点B 处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3 cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是( )
A.13cm B. cm C. cm D. cm
提高题:我国古代有这样一道数学问题:“枯木一根直立地上'高二丈周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?,题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处.则问题中葛藤的最短长度是__________尺.
华东师大版 数学 八年级上册
勾股定理(毕达哥拉斯定理)
如果直角三角形两直角边分别为a、b 斜边为c,那么
a
c
b
A
C
B
即直角三角形两直角边的平方和等于斜边的平方。
结论变形
如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径” ,在花圃内走出了一条“路”,仅仅少走了_____步路, 却踩伤了花草。(假设1米为2步)
“路”
3米
4米
A
B
C
4
5米
一圆柱体的底面周长为20cm,高AB为4cm, BC是上底面的直径 .一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C, 试求出爬行的最短路程.(精确到0.01cm)
沿AB剪开摊开
A
C
B
C
B
A
BC是底面圆的周长的一半
AB是圆柱的高
AC≈10.77cm
如图(1),一圆柱的底面半径为5,BC是底面直径,圆柱高AB为5,求一只蚂蚁从点A出发沿圆柱表面爬行到点C的最短路线。
小明设计了两条路线:
路线1:侧面展开图中的线段AC.如图(2)所示. 用L1表示
设路线1的长度为L1 ,则L12= AC2 =AB2+BC2 =52+(5π)2 =25+25π2
路线2:高线AB+底面直径BC.如图(1)所示.用L2表示
设路线2的长度为L2,则L22 = (AB+BC)2 =(5+10)2=225
∵ L12-L22=25+25π2-225=25(π2-8)>0
∴ L12>L22. ∴ L1>L2
所以选择路线L2较短.
小明对上述结论有些疑惑,于是他把条件改成:“圆柱的底面半径为1,高AB为10”继续按前面的路线进行计算.请你帮小明完成下面的计算:
路线1:L12=AC2= .
路线2:L22=(AB+BC)2 = . ∵ L12 L22, ∴ L1 L2 (填“<”或者 “>”) 所以选择路线 (填L1或L2)较短.
AB2+BC2=102+π2=100+π2
(10+2)2=144
<
<
L1
图①
图②
请你帮小明继续研究:在一般情况下,当圆柱的底面半径为r和高为h满足什么条件时,应如何选择上面的两条路线才能使蚂蚁从点A出发沿圆柱表面爬行到点C的路线最短.(分组讨论,看哪组最快得到答案)
图①
图②
L1=AC
L2=AB+BC
解法如下:
L12=AC2=
AB2+BC2=
h2+(πr)2
L22=(AB+BC)2=
(h+2r)2
L12-L22=h2+(πr)2 -(h+2r)2=r(π2r-4r-4h)=r[(π2-4)r-4h ]
∵L1 >0,L2 >0
∴L1和L2的大小,与L12 和L22的大小关系一样,
又∵r>0, π2-4>0
∴当r= 时,L12 = L22 ,L1= L2,选择路线L1, L2都一样;
当r> 时,L12 >L22 ,L1> L2,选择路线L2较短;
当r< 时,L12< L22 ,L1< L2 ,选择路线L1较短。
图①所示的正方体木块棱长为6cm,沿其相邻三个面的对角线(图中虚线)剪掉一角,得到如图②的几何体,一只蚂蚁沿着图②的几何体表面从顶点A爬行到顶点B的最短距离为 cm.
A(基础练习):
3( + )
c
如图长为3cm,宽为2cm,高为1cm的长方体,蚂蚁沿着表面从点A到点B需要爬行的最短路程是多少?
B( 提高练习):
B
A
1
3
2
前面与上面
AB=
AB=
AB=
B
A
3
2
前面与右侧
1
A
B
下面与右侧
A
B
2
1
3
本节课主要学习了勾股定理的应用——立体图形中最短路径问题,其一般解题思路如下:
1、展:立体图形 → 平面图形;
2、找:最短路线 起点→终点 依据是平面内两点之间线段最短;
3、算:构造出直角三角形,从而利用勾股定理进行计算。
本节课你有什么收获或感想?你还有什么疑问?
基础题:如图是一个三级台阶,它的每一级的长、宽、高分别为20dm、3dm、2dm,点A、点B是这个台阶两个相对的端点,点A有一只蚂蚁,想到点B去吃可口的食物,则蚂蚁沿着台阶面爬到点B最短路程是多少?
中等题:如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3 cm的点B 处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3 cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是( )
A.13cm B. cm C. cm D. cm
提高题:我国古代有这样一道数学问题:“枯木一根直立地上'高二丈周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?,题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处.则问题中葛藤的最短长度是__________尺.
