吉林省长白山第一高中物理必修一课件:2.3 匀变速直线运动的位移与时间的关系
文档属性
| 名称 | 吉林省长白山第一高中物理必修一课件:2.3 匀变速直线运动的位移与时间的关系 |
|
|
| 格式 | zip | ||
| 文件大小 | 618.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2012-10-27 00:00:00 | ||
图片预览





文档简介
课件15张PPT。学案3 匀变速直线运动的位移与时间的关系学点1 匀速直线运动的位移 匀速直线运动中,速度的大小和方向不随时间
变化,我们以横轴表示时间,纵轴表示速度,在平
面直角坐标系中就可作出匀速直线运动的v-t图象。
如图2-3-1所示,它的图象是一条平行于时间轴的
直线。
匀速运动中x=vt。因此位移等于对应时间间隔
内的图线与t轴所包围的“面积”,如图在t0时间内的
位移x=v0t0。它在数值上等于“阴影”的面积。位移
也有正、负,若包围的“面积”在第一象限,则为正;
若在第四象限,则为负。 图2-3-1学点2 匀变速直线运动的位移 (1)匀变速直线运动的位移公式
在v-t图象中位移的大小在数值上等于图线和时间坐标轴包
围的“面积”,即如图2-3-2所示的“梯形”面积。
从v-t图象中,我们也可以直接得出位移的关系式
x=“长方形面积”+“三角形面积”=v0t+[(v-v0)/2]t=v0t+(1/2)at2。
即匀变速直线运动的位移公式为x=v0t+(1/2)at2
①关系式中x、v0、a都是矢量,在应用公式时也要规定正方向。
②匀变速直线运动的平均速度 =x/t=(v0+v)/2 (2)匀变速直线运动的位移在v-t图象中的表示
位移是矢量,有大小也有方向。速度—时间关系v=v0+at,
在v-t图象中,当表示位移的“面积”在t轴上方时,位移取正值,
这表示物体的位移与规定的正方向相同;当表示位移的“面积”
在t轴下方时,位移取负值,这表示物体的位移与规定的正方向
相反。
如图2-3-3所示,在时间0~t1内的位移x1取正值;在t1~t2内的位移x2取负值;物体在时间0~t2内的总位移等于x1和x2的代数和。图2-3-2图2-3-3 对位移和时间关系式的理解
(1)公式中x、v0、a都是矢量,应用时必须选取统一的正方向, 一般选取初速度v0的方向为正方向。
若a与v0同向,a取正值,物体做匀加速直线运动。
若a与v0反向,a取负值,物体做匀减速直线运动。
若位移的计算结果为正值,说明这段时间内位移的方向与规定的正方向相同。
若位移的计算结果为负值,说明这段时间内位移的方向与规定的正方向相反。
(2)此式与v=v0+at是匀变速直线运动的基本公式,应用这两个公式可以解决大多数匀变速直线运动问题。
(3)对于初速度为0(v0=0)的匀变速直线运动,位移公式为x=(1/2)at2。
即位移x与时间t的二次方成正比。 由题图可知,甲做匀加速直线运动,乙做匀速直线运动,速度方向都为正,大小可从v-t图线上直接读出,而位移可以根据图线与坐标轴包围的面积求出。故t=2 s时,v甲=v乙=10 m/s,x甲=10 m,x乙=20 m;t=4 s时,v甲=20 m/s,v乙=10 m/s,x甲=x乙=40 m,故B、D正确。【例1】甲、乙两物体沿同一直线运动的v-t图象如
图2-3-4所示,则( )
A.t=2 s时,两物体速度不同,2 s内的位移相同
B.t=2 s时,两物体速度相同,2 s内的位移不同
C.t=2 s时,两物体速度相同,4 s内的位移不同
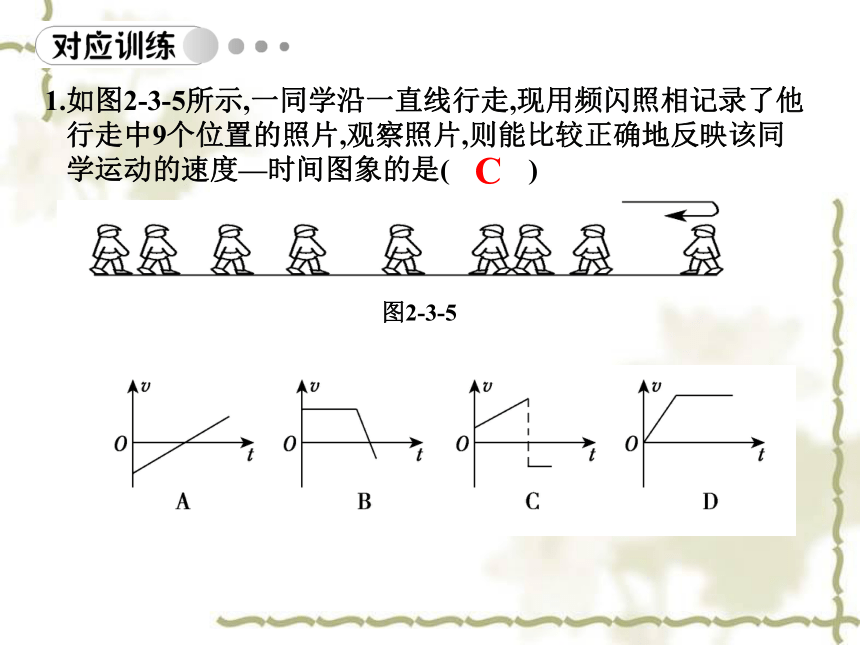
D.t=4 s时,两物体速度不同,4 s内的位移相同B D图2-3-41.如图2-3-5所示,一同学沿一直线行走,现用频闪照相记录了他
行走中9个位置的照片,观察照片,则能比较正确地反映该同
学运动的速度—时间图象的是( )C图2-3-5 (1) 快艇在第8 s末的速度为
v=v0+at1=6 m/s+2×8 m/s=22 m/s
快艇在前8 s内的位移为x1=v0t1+(1/2)at12
=6×8 m+(1/2)×2×82 m=112 m
(2)快艇在第8 s内的初速度即为第7 s末的速度
v2=v0+at2=6 m/s+2×7 m/s=20 m/s
快艇在第8 s内的位移为
x2=v2t3+(1/2)at32
=20×1 m+(1/2)×2×12 m=21 m。【例2】一艘快艇以2 m/s2的加速度在海面上做匀加速直线运动,快艇的
初速度是6 m/s。求:
(1)这艘快艇在8 s末的速度和8 s内的位移;
(2)快艇在第8 s内的位移。(1)22 m/s 112 m
(2)21 m 应用v=v0+at和x=v0t+(1/2)at2求解问题时,必须明确所研究的过程,进而明确其对应的时间、初速度、末速度和加速度。2.钢球在斜槽上做初速度为零的匀加速直线运动。开始
运动后0.2 s内通过的位移是3 cm,则它在第1 s内的位
移是______m。如果斜面长1.5 m,钢球从静止开始由
斜面顶端滚到底端需要的时间是______s。0.75 设汽车刹车时的加速度为a,则有
x2=v0t2+(1/2)at22-[v0t1+(1/2)at12],
其中v0=10 m/s,x2=6.25 m,t2=2 s,t1=1 s代入数据解得a=-2.5 m/s2。
汽车刹车后6 s内的位移
x=v0t+(1/2)at2=10×6 m+(1/2)×(-2.5)×62 m=15 m
进一步求解汽车从刹车到速度减为零经历的时间:
t′=(0-v0)/a=(0-10)/-2.5 s=4 s,
汽车在4 s内的位移
x′=v0t′+(1/2)at′2=20 m。
为什么汽车刹车6 s内的位移比刹车4 s内的位移还要小呢?原因是没有分析清楚汽车的具体运动情况,汽车在刹车后的运动过程中具有-2.5 m/s2的加速度,但在速度减到零以后,汽车将保持静止状态,加速度消失,汽车并不会再倒回来运动。所以处理这类汽车刹车题目要先进行判断:汽车运动到速度为零需多长时间,把这个时间与题目中的时间相比较,再决定用哪种方法求位移。【例3】以10 m/s的速度匀速行驶的汽车,刹车后做匀减速直线运动。若
汽车刹车后第2 s内的位移为6.25 m(刹车时间超过2 s),则刹车后6 s
内汽车的位移是多大? 本题求出a后,后半部分求解如下:
汽车速度减到零所用时间t′=(0-v0)/a=(0-10)/-2.5 s=4 s<6 s,即汽车在4 s末停止后,剩余的2 s处于静止状态,所以刹车后6 s内的位移与4 s内的位移相同,即x=v0t′+(1/2)at′2=20 m。本题中开始求出的位移15 m是错误的,原因是它不符合实际,错误地认为汽车在6s内始终以a=-2.5 m/s2的加速度做匀变速直线运动,即汽车4 s末速度减为零后又反向后退了2 s,所以导致出现了前面的矛盾。20 m3.骑自行车的人以5 m/s的初速度匀减速地上一
个斜坡,加速度的大小为0.4 m/s2,斜坡长30
m,骑自行车的人通过斜坡需要多少时间?10 s学点3 用图象表示位移 (1)位移图象的意义
表示物体离开t=0时刻所处位置的位移随
时间变化的规律,在图2-3-6中坐标点(t1,x1)
表示t1时刻物体离开初位置(t=0)的位移为x1,
在t1~t2时间内的位移为Δx=x2-x1。 (2)速度在x-t图象中的体现
在x-t图象中,任意一点处的切线斜率表示该时刻物体的速度。在图2-3-6中,t1、t2两时刻的速度v1、v2满足v1 所示,试回答以下问题。
(1)0~2 s和2 s~4 s内质点做什么运动?
(2)在0~2 s内、0~4 s内和2~4 s内的位移分别为多
少? (1)在0~2 s内,x-t图象为倾斜直线;表示物体做匀速直线运动,速度v=Δx/t=(10/2) m/s=5 m/s
在2~4 s内物体始终处于x=10 m处不动。
(2)在0~2 s内位移为Δx1=10 m;
在0~4 s内位移为Δx2=10 m;
在2~4 s内位移为Δx3=0。(1)0~2 s内物体做匀速运动,且速度v=5 m/s
在2~4 s内物体静止不动
(2)10 m,10 m,0图2-3-74.试画出按v=(2+2t) m/s规律匀加速运动的位移图象。图见解析1.某一做直线运动的质点的位移随时间变化的关系式为x=4t+2t2,x与t
的单位分别是m和s,则质点的初速度和加速度分别是( )
A.4 m/s和2 m/s2 B.0和4 m/s2
C.4 m/s和4 m/s2 D.4 m/s和02.若一质点从t=0开始由原点出发沿直线运动,其速
度—时间图象如图2-3-8所示,则该质点( )
A.t=1 s时离原点最远
B.t=2 s时离原点最远
C.t=3 s时回到原点
D.t=4 s时回到原点,路程为10 mCBD图2-3-83.以18 m/s的速度行驶的汽车,紧急刹车后做匀减速直线运动,其加速度
的大小为6 m/s2,求汽车在6 s内通过的距离。27 m
变化,我们以横轴表示时间,纵轴表示速度,在平
面直角坐标系中就可作出匀速直线运动的v-t图象。
如图2-3-1所示,它的图象是一条平行于时间轴的
直线。
匀速运动中x=vt。因此位移等于对应时间间隔
内的图线与t轴所包围的“面积”,如图在t0时间内的
位移x=v0t0。它在数值上等于“阴影”的面积。位移
也有正、负,若包围的“面积”在第一象限,则为正;
若在第四象限,则为负。 图2-3-1学点2 匀变速直线运动的位移 (1)匀变速直线运动的位移公式
在v-t图象中位移的大小在数值上等于图线和时间坐标轴包
围的“面积”,即如图2-3-2所示的“梯形”面积。
从v-t图象中,我们也可以直接得出位移的关系式
x=“长方形面积”+“三角形面积”=v0t+[(v-v0)/2]t=v0t+(1/2)at2。
即匀变速直线运动的位移公式为x=v0t+(1/2)at2
①关系式中x、v0、a都是矢量,在应用公式时也要规定正方向。
②匀变速直线运动的平均速度 =x/t=(v0+v)/2 (2)匀变速直线运动的位移在v-t图象中的表示
位移是矢量,有大小也有方向。速度—时间关系v=v0+at,
在v-t图象中,当表示位移的“面积”在t轴上方时,位移取正值,
这表示物体的位移与规定的正方向相同;当表示位移的“面积”
在t轴下方时,位移取负值,这表示物体的位移与规定的正方向
相反。
如图2-3-3所示,在时间0~t1内的位移x1取正值;在t1~t2内的位移x2取负值;物体在时间0~t2内的总位移等于x1和x2的代数和。图2-3-2图2-3-3 对位移和时间关系式的理解
(1)公式中x、v0、a都是矢量,应用时必须选取统一的正方向, 一般选取初速度v0的方向为正方向。
若a与v0同向,a取正值,物体做匀加速直线运动。
若a与v0反向,a取负值,物体做匀减速直线运动。
若位移的计算结果为正值,说明这段时间内位移的方向与规定的正方向相同。
若位移的计算结果为负值,说明这段时间内位移的方向与规定的正方向相反。
(2)此式与v=v0+at是匀变速直线运动的基本公式,应用这两个公式可以解决大多数匀变速直线运动问题。
(3)对于初速度为0(v0=0)的匀变速直线运动,位移公式为x=(1/2)at2。
即位移x与时间t的二次方成正比。 由题图可知,甲做匀加速直线运动,乙做匀速直线运动,速度方向都为正,大小可从v-t图线上直接读出,而位移可以根据图线与坐标轴包围的面积求出。故t=2 s时,v甲=v乙=10 m/s,x甲=10 m,x乙=20 m;t=4 s时,v甲=20 m/s,v乙=10 m/s,x甲=x乙=40 m,故B、D正确。【例1】甲、乙两物体沿同一直线运动的v-t图象如
图2-3-4所示,则( )
A.t=2 s时,两物体速度不同,2 s内的位移相同
B.t=2 s时,两物体速度相同,2 s内的位移不同
C.t=2 s时,两物体速度相同,4 s内的位移不同
D.t=4 s时,两物体速度不同,4 s内的位移相同B D图2-3-41.如图2-3-5所示,一同学沿一直线行走,现用频闪照相记录了他
行走中9个位置的照片,观察照片,则能比较正确地反映该同
学运动的速度—时间图象的是( )C图2-3-5 (1) 快艇在第8 s末的速度为
v=v0+at1=6 m/s+2×8 m/s=22 m/s
快艇在前8 s内的位移为x1=v0t1+(1/2)at12
=6×8 m+(1/2)×2×82 m=112 m
(2)快艇在第8 s内的初速度即为第7 s末的速度
v2=v0+at2=6 m/s+2×7 m/s=20 m/s
快艇在第8 s内的位移为
x2=v2t3+(1/2)at32
=20×1 m+(1/2)×2×12 m=21 m。【例2】一艘快艇以2 m/s2的加速度在海面上做匀加速直线运动,快艇的
初速度是6 m/s。求:
(1)这艘快艇在8 s末的速度和8 s内的位移;
(2)快艇在第8 s内的位移。(1)22 m/s 112 m
(2)21 m 应用v=v0+at和x=v0t+(1/2)at2求解问题时,必须明确所研究的过程,进而明确其对应的时间、初速度、末速度和加速度。2.钢球在斜槽上做初速度为零的匀加速直线运动。开始
运动后0.2 s内通过的位移是3 cm,则它在第1 s内的位
移是______m。如果斜面长1.5 m,钢球从静止开始由
斜面顶端滚到底端需要的时间是______s。0.75 设汽车刹车时的加速度为a,则有
x2=v0t2+(1/2)at22-[v0t1+(1/2)at12],
其中v0=10 m/s,x2=6.25 m,t2=2 s,t1=1 s代入数据解得a=-2.5 m/s2。
汽车刹车后6 s内的位移
x=v0t+(1/2)at2=10×6 m+(1/2)×(-2.5)×62 m=15 m
进一步求解汽车从刹车到速度减为零经历的时间:
t′=(0-v0)/a=(0-10)/-2.5 s=4 s,
汽车在4 s内的位移
x′=v0t′+(1/2)at′2=20 m。
为什么汽车刹车6 s内的位移比刹车4 s内的位移还要小呢?原因是没有分析清楚汽车的具体运动情况,汽车在刹车后的运动过程中具有-2.5 m/s2的加速度,但在速度减到零以后,汽车将保持静止状态,加速度消失,汽车并不会再倒回来运动。所以处理这类汽车刹车题目要先进行判断:汽车运动到速度为零需多长时间,把这个时间与题目中的时间相比较,再决定用哪种方法求位移。【例3】以10 m/s的速度匀速行驶的汽车,刹车后做匀减速直线运动。若
汽车刹车后第2 s内的位移为6.25 m(刹车时间超过2 s),则刹车后6 s
内汽车的位移是多大? 本题求出a后,后半部分求解如下:
汽车速度减到零所用时间t′=(0-v0)/a=(0-10)/-2.5 s=4 s<6 s,即汽车在4 s末停止后,剩余的2 s处于静止状态,所以刹车后6 s内的位移与4 s内的位移相同,即x=v0t′+(1/2)at′2=20 m。本题中开始求出的位移15 m是错误的,原因是它不符合实际,错误地认为汽车在6s内始终以a=-2.5 m/s2的加速度做匀变速直线运动,即汽车4 s末速度减为零后又反向后退了2 s,所以导致出现了前面的矛盾。20 m3.骑自行车的人以5 m/s的初速度匀减速地上一
个斜坡,加速度的大小为0.4 m/s2,斜坡长30
m,骑自行车的人通过斜坡需要多少时间?10 s学点3 用图象表示位移 (1)位移图象的意义
表示物体离开t=0时刻所处位置的位移随
时间变化的规律,在图2-3-6中坐标点(t1,x1)
表示t1时刻物体离开初位置(t=0)的位移为x1,
在t1~t2时间内的位移为Δx=x2-x1。 (2)速度在x-t图象中的体现
在x-t图象中,任意一点处的切线斜率表示该时刻物体的速度。在图2-3-6中,t1、t2两时刻的速度v1、v2满足v1
(1)0~2 s和2 s~4 s内质点做什么运动?
(2)在0~2 s内、0~4 s内和2~4 s内的位移分别为多
少? (1)在0~2 s内,x-t图象为倾斜直线;表示物体做匀速直线运动,速度v=Δx/t=(10/2) m/s=5 m/s
在2~4 s内物体始终处于x=10 m处不动。
(2)在0~2 s内位移为Δx1=10 m;
在0~4 s内位移为Δx2=10 m;
在2~4 s内位移为Δx3=0。(1)0~2 s内物体做匀速运动,且速度v=5 m/s
在2~4 s内物体静止不动
(2)10 m,10 m,0图2-3-74.试画出按v=(2+2t) m/s规律匀加速运动的位移图象。图见解析1.某一做直线运动的质点的位移随时间变化的关系式为x=4t+2t2,x与t
的单位分别是m和s,则质点的初速度和加速度分别是( )
A.4 m/s和2 m/s2 B.0和4 m/s2
C.4 m/s和4 m/s2 D.4 m/s和02.若一质点从t=0开始由原点出发沿直线运动,其速
度—时间图象如图2-3-8所示,则该质点( )
A.t=1 s时离原点最远
B.t=2 s时离原点最远
C.t=3 s时回到原点
D.t=4 s时回到原点,路程为10 mCBD图2-3-83.以18 m/s的速度行驶的汽车,紧急刹车后做匀减速直线运动,其加速度
的大小为6 m/s2,求汽车在6 s内通过的距离。27 m
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
