吉林省长白山第一高中物理必修一课件:3.5 力 的 分 解
文档属性
| 名称 | 吉林省长白山第一高中物理必修一课件:3.5 力 的 分 解 |
|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2012-10-27 00:00:00 | ||
图片预览



文档简介
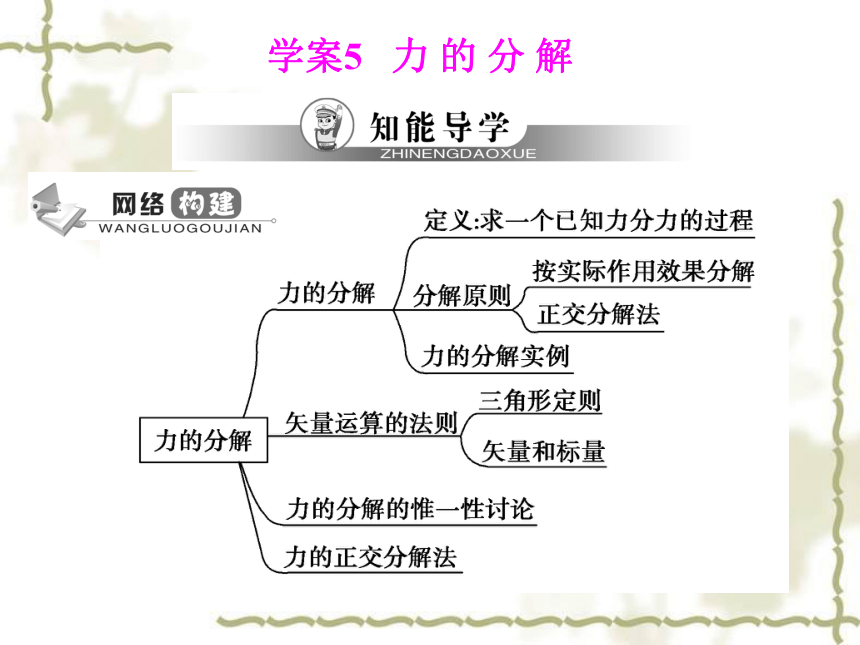
课件13张PPT。学案5 力 的 分 解学点1 力的分解 (5)力的分解的方法和步骤
①首先是要根据这个力的实际作用效果确定两个实际
分力的方向。
②再根据两个实际分力方向作平行四边形,已知力为
对角线,实际分力为邻边。
③然后根据平行四边形知识和相关的数学知识,求出
两分力的大小和方向。图3-5-1 (4)如果没有其他限制,对于一条对角线,可以作出无数个不同的平行四边形,如图3-5-1所示。即同一个力F可以分解成无数对大小、方向不同的分力。 (1)定义:作用在物体上的一个力的作用效果,与几个力的作用效果相同,则这几个力叫做该力的分力。已知合力求分力叫做力的分解。
(2)力的分解是力的合成的逆运算。
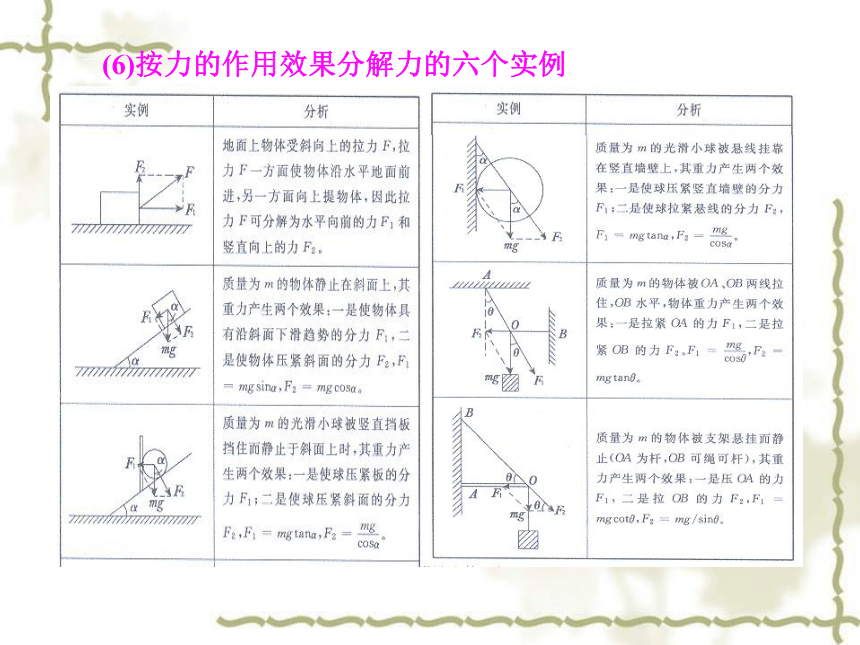
(3)力的分解遵循平行四边形定则:把一个已知力作为平行四边形的对角线,则与已知力共点的平行四边形的两个邻边就表示已知力的两个分力。(6)按力的作用效果分解力的六个实例 物体的重力产生两个效果:拉紧绳子和挤压墙壁。所以将重力沿着这两个方向进行分解,其受力如图3-5-3所示。
通过解三角形可以求得F2=Gtan?=mgtan?。 F1=G/cos?=mg/cos?。
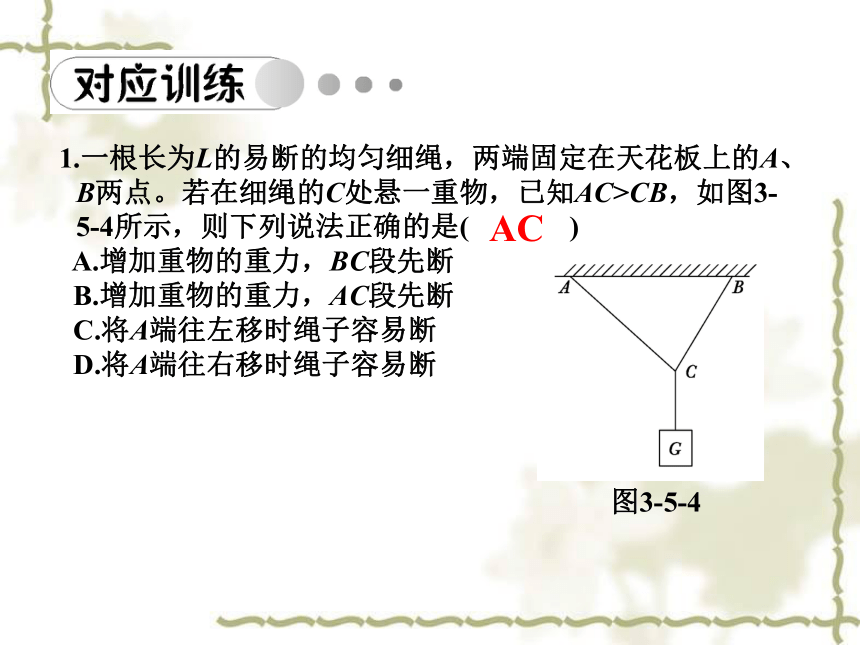
足球对绳的拉力大小等于绳对足球的拉力,即F1′=F1=mg/cos?,足球对墙壁的压力大小等于F2′=F2=mgtan?。【例1】沿光滑的墙壁用网兜把一个足球挂在A点,如图3-5-2所示,足球的质量为m,网兜的质量不计,足球与墙壁的接触点为B,悬绳与墙壁的夹角为?。求足球对绳的拉力和对墙壁的压力的大小。mg/cos? mgtan?图3-5-3图3-5-21.一根长为L的易断的均匀细绳,两端固定在天花板上的A、B两点。若在细绳的C处悬一重物,已知AC>CB,如图3-5-4所示,则下列说法正确的是( )
A.增加重物的重力,BC段先断
B.增加重物的重力,AC段先断
C.将A端往左移时绳子容易断
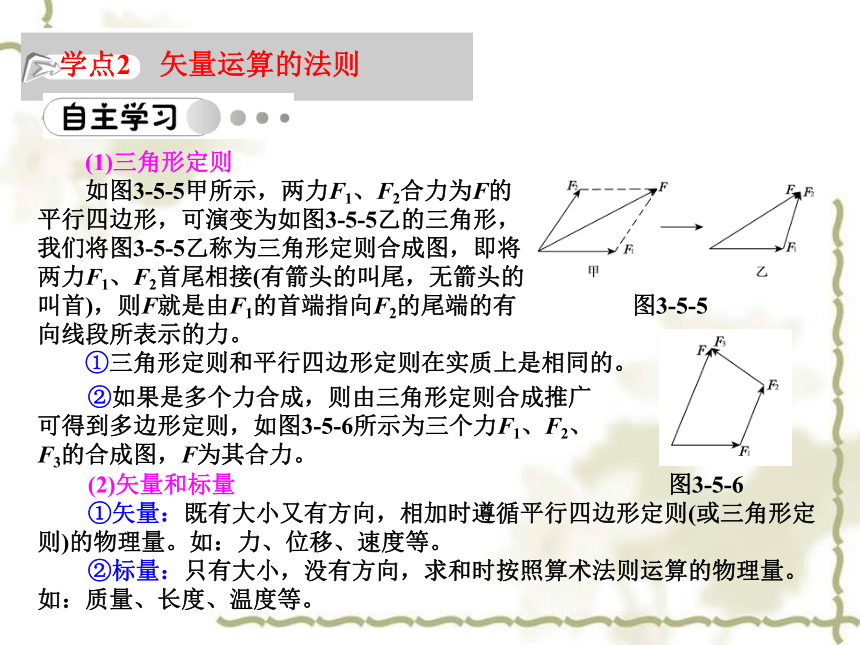
D.将A端往右移时绳子容易断AC图3-5-4学点2 矢量运算的法则 (1)三角形定则
如图3-5-5甲所示,两力F1、F2合力为F的
平行四边形,可演变为如图3-5-5乙的三角形,
我们将图3-5-5乙称为三角形定则合成图,即将
两力F1、F2首尾相接(有箭头的叫尾,无箭头的
叫首),则F就是由F1的首端指向F2的尾端的有
向线段所表示的力。
①三角形定则和平行四边形定则在实质上是相同的。(2)矢量和标量
①矢量:既有大小又有方向,相加时遵循平行四边形定则(或三角形定则)的物理量。如:力、位移、速度等。
②标量:只有大小,没有方向,求和时按照算术法则运算的物理量。如:质量、长度、温度等。②如果是多个力合成,则由三角形定则合成推广可得到多边形定则,如图3-5-6所示为三个力F1、F2、F3的合成图,F为其合力。图3-5-6图3-5-5 根据题意,作出矢量三角形,如图3-5-7所示,因为 /3F>F2,从图上可以看出,F1的大小有两个可能值。
由直角三角形OAD,可知OA= 。
由直角三角形ABD,可知AB= 。
由图的对称性可知AC=AB= /6F。
则分力F1= /2F- /6F= /3F,
F′1= /2F+ /6F=(2/3) F。【例2】已知力F的一个分力F1跟F成30°角,大小未知,另一分力F2的大小为 /3F,方向未知,则F1的大小可能是( )
A. F/3 B. F/2 C.2 F/3 D. FAC图3-5-72.一架质量为4 000 kg的歼击机,在5.0×105 N推力作用下由静止开始起飞,飞行方向与水平方向成30°角,飞行加速度为10 m/s2,如图3-5-8所示,求:
(1)起飞20 s后,飞机距离地面的高度;
(2)起飞20 s后,飞机在水平方向的分速
度vx和竖直方向的分速度vy;(1)1 000 m (2) vy=100 m/s图3-5-8学点3 力的正交分解法在力的分解中,除按力的实际作用效果分解外,有时根据解决问题的需要,进行正交分解。
(1)正交分解法:把力沿着两个选定的相互垂直的方向分解的方法。
(2)正交分解法求多个力的合力
当物体受到多个力的作用,并且这几个力只共面不共线时,用平行四边形定则求其合力困难较大。为此,可以建立一个直角坐标系,先将各力正交分解在两条互相垂直的坐标轴下,分别求出两个不同方向上的合力Fx和Fy,然后再求Fx、Fy的合力。具体步骤如下:
①建立坐标系,以共点力的作用点为坐标原点建立直角坐标系,坐标轴x和y轴的选择应使尽量多的力落在坐标轴上;②正交分解各力,即将每一个不在坐标轴上的力分解到x和y坐标轴上,并求出各分力的大小,如图3-5-9所示;图3-5-9③分别求x轴和y轴上各力的合力,即Fx=F1x+F2x+…,
Fy=F1y+F2y+…;
④求Fx与Fy的合力即为共点力的合力。合力的大小:F= ,合力F的方向与x轴的夹角?=arctan(Fy/Fx)。 应用正交分解法将各力先分解,再合成,在建立坐标系时尽量使各力与坐标轴的夹角为特殊角。
以F2方向为x轴的正方向,如图3-5-11所示,则F1、F3、F4向两坐标轴上分解得
F1x=F1cos60°=20×1/2 N=10 N,
F1y=F1sin60°=20× /3 N=10 N;
F2x=20 N,F2y=0;【例3】如图3-5-10所示,力F1、F2、F3、F4在同一平面内构成共点力,其中F1=20 N、F2=20 N、F3=20 N、F4=
20 N,各力之间的夹角在图中已标出,求这四个共点力的合力大小和方向。图3-5-10图3-5-1120 N,与F3方向一致F3x=F3cos45°=20 × /2 N=20 N,
F3y=-F3cos45°=-20 × /2 N=-20 N,
F4x=-F4sin60°=-20 × /2 N=-30 N,
F4y=-F4cos60°=-20 ×1/2 N=-10 N。
四个力在x轴上合力为Fx=F1x+F2x+F3x+F4x=20 N,
在y轴上合力为Fy=F1y+F2y+F3y+F4y=-20 N,
四个力的合力F= =20 N。
合力方向与F3方向一致。1.如图3-5-12所示,将力F分解为F1、F2两个分力,则以下说法中正确的是( )
A.F1、F2的合力就是F
B.由F求F1、F2叫力的分解,由F1、F2求F叫力的合成
C.力的合成和分解都遵守平行四边形定则
D.F1、F2、F的大小关系应满足|F1-F2|≤F≤F1+F22.在倾角?=30°的斜面上有一块竖直可旋转的挡板,在挡板和斜面之间放有一个重为G=20 N的光滑圆球,如图3-5-13所示,试求这个球对斜面的压力和对挡板的压力。ABCD40 /3 N;20 /3 N图3-5-12图3-5-13
①首先是要根据这个力的实际作用效果确定两个实际
分力的方向。
②再根据两个实际分力方向作平行四边形,已知力为
对角线,实际分力为邻边。
③然后根据平行四边形知识和相关的数学知识,求出
两分力的大小和方向。图3-5-1 (4)如果没有其他限制,对于一条对角线,可以作出无数个不同的平行四边形,如图3-5-1所示。即同一个力F可以分解成无数对大小、方向不同的分力。 (1)定义:作用在物体上的一个力的作用效果,与几个力的作用效果相同,则这几个力叫做该力的分力。已知合力求分力叫做力的分解。
(2)力的分解是力的合成的逆运算。
(3)力的分解遵循平行四边形定则:把一个已知力作为平行四边形的对角线,则与已知力共点的平行四边形的两个邻边就表示已知力的两个分力。(6)按力的作用效果分解力的六个实例 物体的重力产生两个效果:拉紧绳子和挤压墙壁。所以将重力沿着这两个方向进行分解,其受力如图3-5-3所示。
通过解三角形可以求得F2=Gtan?=mgtan?。 F1=G/cos?=mg/cos?。
足球对绳的拉力大小等于绳对足球的拉力,即F1′=F1=mg/cos?,足球对墙壁的压力大小等于F2′=F2=mgtan?。【例1】沿光滑的墙壁用网兜把一个足球挂在A点,如图3-5-2所示,足球的质量为m,网兜的质量不计,足球与墙壁的接触点为B,悬绳与墙壁的夹角为?。求足球对绳的拉力和对墙壁的压力的大小。mg/cos? mgtan?图3-5-3图3-5-21.一根长为L的易断的均匀细绳,两端固定在天花板上的A、B两点。若在细绳的C处悬一重物,已知AC>CB,如图3-5-4所示,则下列说法正确的是( )
A.增加重物的重力,BC段先断
B.增加重物的重力,AC段先断
C.将A端往左移时绳子容易断
D.将A端往右移时绳子容易断AC图3-5-4学点2 矢量运算的法则 (1)三角形定则
如图3-5-5甲所示,两力F1、F2合力为F的
平行四边形,可演变为如图3-5-5乙的三角形,
我们将图3-5-5乙称为三角形定则合成图,即将
两力F1、F2首尾相接(有箭头的叫尾,无箭头的
叫首),则F就是由F1的首端指向F2的尾端的有
向线段所表示的力。
①三角形定则和平行四边形定则在实质上是相同的。(2)矢量和标量
①矢量:既有大小又有方向,相加时遵循平行四边形定则(或三角形定则)的物理量。如:力、位移、速度等。
②标量:只有大小,没有方向,求和时按照算术法则运算的物理量。如:质量、长度、温度等。②如果是多个力合成,则由三角形定则合成推广可得到多边形定则,如图3-5-6所示为三个力F1、F2、F3的合成图,F为其合力。图3-5-6图3-5-5 根据题意,作出矢量三角形,如图3-5-7所示,因为 /3F>F2,从图上可以看出,F1的大小有两个可能值。
由直角三角形OAD,可知OA= 。
由直角三角形ABD,可知AB= 。
由图的对称性可知AC=AB= /6F。
则分力F1= /2F- /6F= /3F,
F′1= /2F+ /6F=(2/3) F。【例2】已知力F的一个分力F1跟F成30°角,大小未知,另一分力F2的大小为 /3F,方向未知,则F1的大小可能是( )
A. F/3 B. F/2 C.2 F/3 D. FAC图3-5-72.一架质量为4 000 kg的歼击机,在5.0×105 N推力作用下由静止开始起飞,飞行方向与水平方向成30°角,飞行加速度为10 m/s2,如图3-5-8所示,求:
(1)起飞20 s后,飞机距离地面的高度;
(2)起飞20 s后,飞机在水平方向的分速
度vx和竖直方向的分速度vy;(1)1 000 m (2) vy=100 m/s图3-5-8学点3 力的正交分解法在力的分解中,除按力的实际作用效果分解外,有时根据解决问题的需要,进行正交分解。
(1)正交分解法:把力沿着两个选定的相互垂直的方向分解的方法。
(2)正交分解法求多个力的合力
当物体受到多个力的作用,并且这几个力只共面不共线时,用平行四边形定则求其合力困难较大。为此,可以建立一个直角坐标系,先将各力正交分解在两条互相垂直的坐标轴下,分别求出两个不同方向上的合力Fx和Fy,然后再求Fx、Fy的合力。具体步骤如下:
①建立坐标系,以共点力的作用点为坐标原点建立直角坐标系,坐标轴x和y轴的选择应使尽量多的力落在坐标轴上;②正交分解各力,即将每一个不在坐标轴上的力分解到x和y坐标轴上,并求出各分力的大小,如图3-5-9所示;图3-5-9③分别求x轴和y轴上各力的合力,即Fx=F1x+F2x+…,
Fy=F1y+F2y+…;
④求Fx与Fy的合力即为共点力的合力。合力的大小:F= ,合力F的方向与x轴的夹角?=arctan(Fy/Fx)。 应用正交分解法将各力先分解,再合成,在建立坐标系时尽量使各力与坐标轴的夹角为特殊角。
以F2方向为x轴的正方向,如图3-5-11所示,则F1、F3、F4向两坐标轴上分解得
F1x=F1cos60°=20×1/2 N=10 N,
F1y=F1sin60°=20× /3 N=10 N;
F2x=20 N,F2y=0;【例3】如图3-5-10所示,力F1、F2、F3、F4在同一平面内构成共点力,其中F1=20 N、F2=20 N、F3=20 N、F4=
20 N,各力之间的夹角在图中已标出,求这四个共点力的合力大小和方向。图3-5-10图3-5-1120 N,与F3方向一致F3x=F3cos45°=20 × /2 N=20 N,
F3y=-F3cos45°=-20 × /2 N=-20 N,
F4x=-F4sin60°=-20 × /2 N=-30 N,
F4y=-F4cos60°=-20 ×1/2 N=-10 N。
四个力在x轴上合力为Fx=F1x+F2x+F3x+F4x=20 N,
在y轴上合力为Fy=F1y+F2y+F3y+F4y=-20 N,
四个力的合力F= =20 N。
合力方向与F3方向一致。1.如图3-5-12所示,将力F分解为F1、F2两个分力,则以下说法中正确的是( )
A.F1、F2的合力就是F
B.由F求F1、F2叫力的分解,由F1、F2求F叫力的合成
C.力的合成和分解都遵守平行四边形定则
D.F1、F2、F的大小关系应满足|F1-F2|≤F≤F1+F22.在倾角?=30°的斜面上有一块竖直可旋转的挡板,在挡板和斜面之间放有一个重为G=20 N的光滑圆球,如图3-5-13所示,试求这个球对斜面的压力和对挡板的压力。ABCD40 /3 N;20 /3 N图3-5-12图3-5-13
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
