3.5圆柱和圆锥回顾整理(课件)人教版 数学六年级下册(共26张PPT)
文档属性
| 名称 | 3.5圆柱和圆锥回顾整理(课件)人教版 数学六年级下册(共26张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 13:10:54 | ||
图片预览


文档简介
(共26张PPT)
六年级下册
2.5 圆柱和圆锥回顾整理
学习目标
1、了解圆柱、圆锥各部分名称, 掌握圆柱、圆锥的特征。
2、掌握侧面积和表面积的计算方法,能正确运用公式计算圆柱的侧面积和表面积。
3、会用圆柱的体积计算圆柱形物体的体积和容积,运用公式解决一些简单的问题。
4、会运用公式计算圆锥的体积。
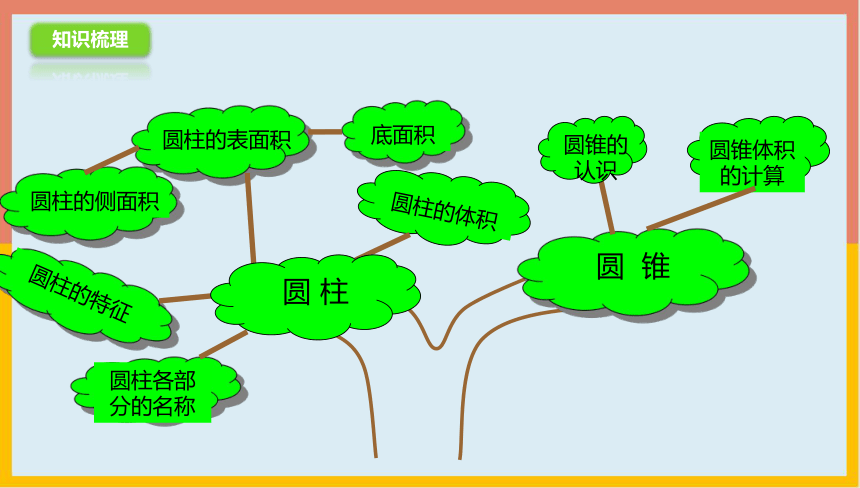
圆 锥
圆锥体积的计算
圆锥的认识
底面积
圆柱各部分的名称
圆柱的表面积
圆柱的体积
圆柱的侧面积
圆柱的特征
圆 柱
知识梳理
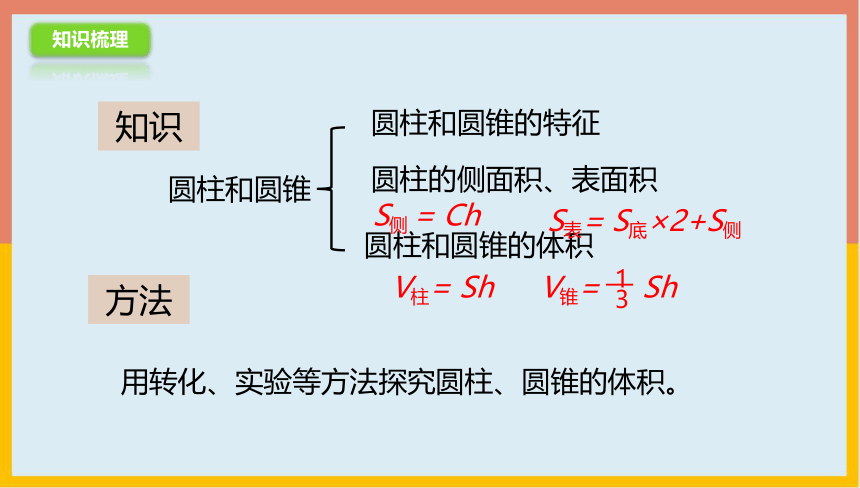
圆柱和圆锥
圆柱的侧面积、表面积
圆柱和圆锥的特征
圆柱和圆锥的体积
S侧 = Ch
V柱= Sh
S表= S底×2+S侧
1
3
V锥= Sh
知识
方法
用转化、实验等方法探究圆柱、圆锥的体积。
知识梳理
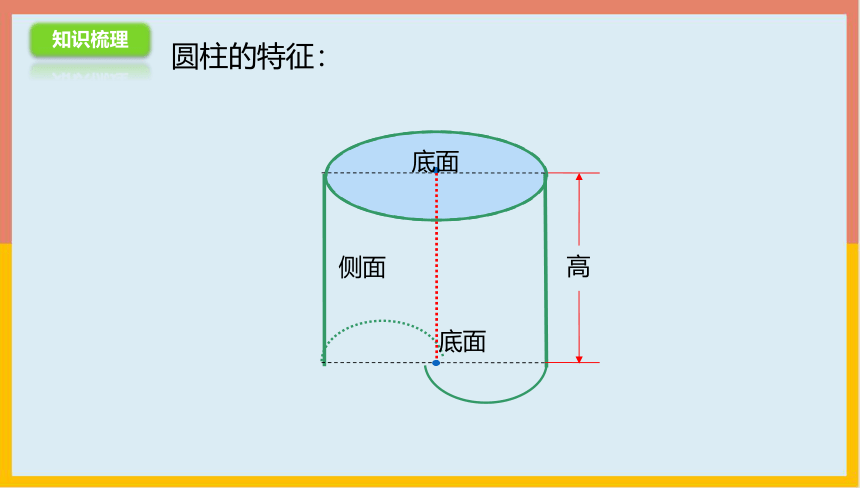
底面
底面
高
侧面
圆柱的特征:
知识梳理
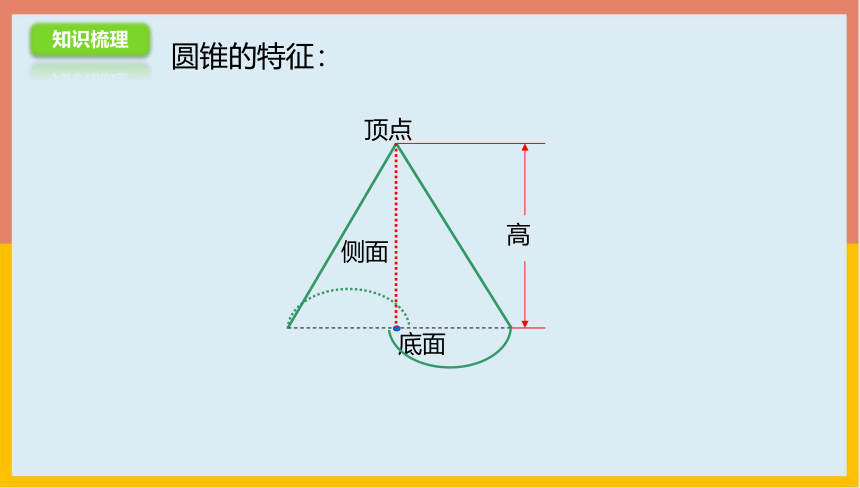
高
底面
侧面
顶点
圆锥的特征:
知识梳理
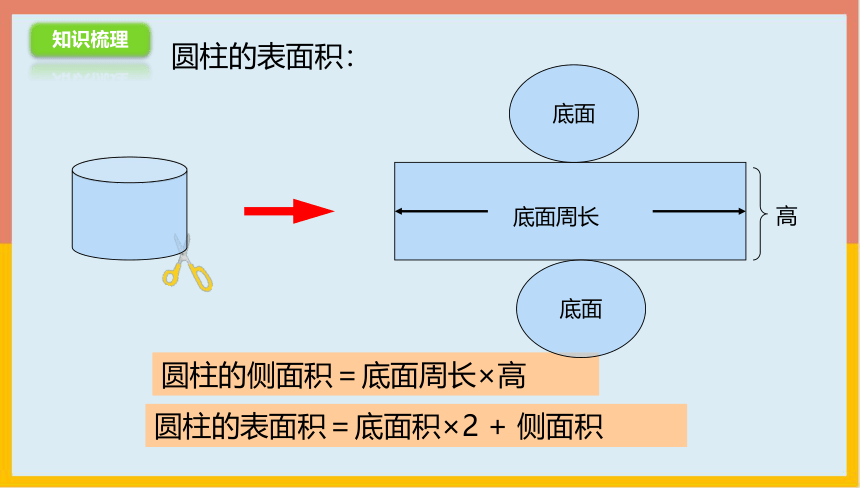
圆柱的侧面积=底面周长×高
底面
底面
高
底面周长
圆柱的表面积=底面积×2 + 侧面积
圆柱的表面积:
知识梳理
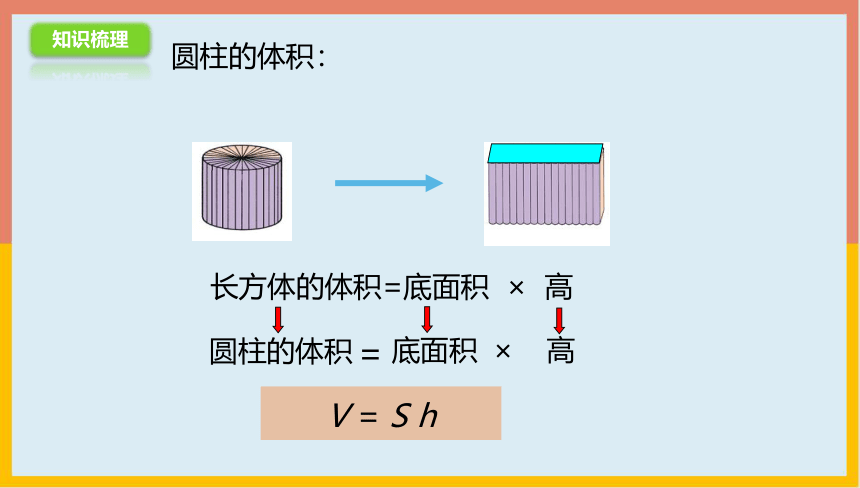
圆柱的体积:
V = S h
底面积
高
圆柱的体积
=
×
长方体的体积=底面积 × 高
知识梳理
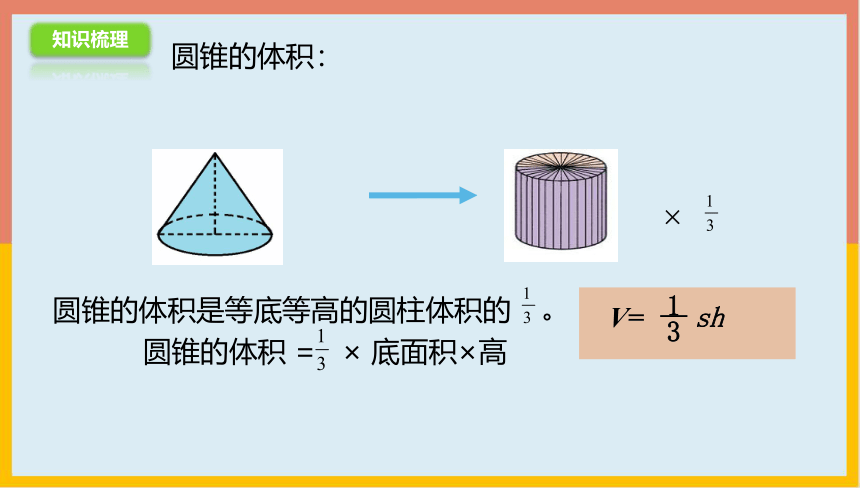
圆锥的体积 = × 底面积×高
Ⅴ= sh
1
3
圆锥的体积是等底等高的圆柱体积的 。
圆锥的体积:
×
知识梳理
图形 特征 侧面积、
表面积公式 体积公式
圆柱
圆锥 -----
两个同样大小的
底面,一个侧面,
有无数条高。
一个底面,一个
侧面,一个顶点,
只能画一条高。
V柱=Sh
V锥= Sh
1
3
S侧=Ch
S表=S底×2+S侧
知识梳理
长方体、正方体体积公式的推导过程:
现实问题
数学问题
联想已有
知识经验
知识梳理
寻找方法
知识梳理
归纳结论
解决问题
解释应用
知识梳理
方法整理:
现实问题
怎样求圆柱形包装盒的体积?
数学问题
联想已有知识经验
归纳结论
解决问题、解释应用
产生新问题
怎样求圆柱体的体积?
推导圆面积公式时,是把圆转化成近似的长方形,推导圆柱体体积计算公式时,可否把它转化成长方体来研究呢?
猜想、验证、总结体积公式:V=Sh
运用公式求出圆柱体的体积,解决求冰淇淋包装盒的问题。
在解决问题的过程中产生新问题。
寻找方法
分一分,
切一切,
拼一拼。
知识梳理
圆柱的体积:
(60÷2)2×3.14×60
= 900 ×3.14×60
= 169560(立方厘米)
169560立方厘米=169.56立方分米
60厘米
60厘米
难点突破
李老师做一件冰雕作品,要将两个棱长为60厘米的正方体冰块分别雕成最大的圆柱和圆锥。它们的体积各是多少立方分米?
难点突破
169.56 ×
圆锥的体积:
1
3
答:圆柱和圆锥的体积分别是
169.56立方分米和56.52立方分米。
60厘米
60厘米
=56.52(立方分米)
李老师做一件冰雕作品,要将两个棱长为60厘米的正方体冰块分别雕成最大的圆柱和圆锥。它们的体积各是多少立方分米?
2.1米
10米
6米
(1)这个粮仓的占地面积有多大?
(2)它的容积是多少立方米?
(墙壁的厚度忽略不计。)
(1)(10÷2)2×3.14=78.5(平方米)
答:粮仓的占地面积是78.5平方米。
= 471+54.95
= 525.95(立方米)
答:它的容积是525.95立方米。
(2)78.5×6+78.5×2.1×
难点突破
圆柱的认识
圆 柱
圆柱的表面积
圆柱的侧面积
底面积
圆柱的体积
圆 锥
圆锥的认识
圆锥体积的计算
回顾整理
本课小结
3dm
8cm
6m
10dm
50.24cm2
4m
28.26dm2
12.56m2
226.08cm2
244.92dm2
113.04m2
251.2cm3
37.68m3
150.72m3
填一填。
随堂检测
一个圆柱形的水池,从里面量得底面直径是16米,深为1.5米。 它的容积是多少立方米?它的四周和底面抹有水泥,至少用了多少千克水泥?(每平方米用水泥10千克。)
水池的容积:
(16÷2)2×3.14×1.5
= 82 ×3.14×1.5
= 301.44(立方米)
答:水池的容积是301.44立方米。
水泥的重量:
(16÷2)2×3.14+16×3.14×1.5
= 82 ×3.14+50.24×1.5
= 276.32(平方米)
答:至少用了2763.2千克水泥。
276.32×10 = 2763.2(千克)
随堂检测
一根竹筒从里面量直径为4厘米,长为10厘米。把大米装至竹筒长的 处做米饭,如果每立方厘米大米约重3克,这根竹筒里的大米大约重多少克?
(只列式不计算。)
3
5
3×3.14×(4÷2)2×10×
3
5
随堂检测
孔庙大成殿前檐有10根石雕龙柱,高6米,直径为0.8米。已知每立方米石料约重2.7吨,这些柱子大约重多少吨?(只列式不计算。)
(0.8÷2)2×3.14×6×10×2.7
随堂检测
30cm
2m
结合圆柱和圆锥的知识,联系实际,展开想象的翅膀,看看你能提出什么问题,你能列出算式吗?
(1)圆柱的表面积是多少平方厘米?
(2)圆柱的体积是多少立方厘米?
(3)如果把它削成一个最大圆锥体,圆锥体的体积是多少立方厘米?
3.14×(30÷2)2 ×200
3.14×30×200+3.14×(30÷2)2 ×2
1
3
×3.14×(30÷2)2 ×200
随堂检测
随堂检测
如果每人每天刷牙要用2厘米长的牙膏,那么1个月(30)天要用多少立方厘米的牙膏?如果管口的直径减少1毫米,那么1个月(30)大约节省多少立方厘米的牙膏?(得数保留整数)
6mm=0.3cm
3.14 × (0.6 ÷ 2)2 × 2 × 30
=3.14 × 0.32 × 2 × 30
=16.956(cm2)
≈17 (cm2 )
答:1个月大约要用17cm2 的牙膏。
6-1=5(mm)5mm=0.5cm
3.14 × (0.5 ÷ 2)2 × 2 × 30
=3.14 × 0.252 × 2 × 30
=11.775(cm2)
≈12(cm2 )
17 – 12 = 5cm2
答:1个月大约节约5cm2 的牙膏。
作业布置
(1)做一个雨量器的外壳(无盖),至少需要多少平方厘米材料?(可以用计算器计算)
(2)储水瓶里一共接了多少毫升雨水?
空白演示
单击输入您的封面副标题
谢 谢 聆 听
六年级下册
2.5 圆柱和圆锥回顾整理
学习目标
1、了解圆柱、圆锥各部分名称, 掌握圆柱、圆锥的特征。
2、掌握侧面积和表面积的计算方法,能正确运用公式计算圆柱的侧面积和表面积。
3、会用圆柱的体积计算圆柱形物体的体积和容积,运用公式解决一些简单的问题。
4、会运用公式计算圆锥的体积。
圆 锥
圆锥体积的计算
圆锥的认识
底面积
圆柱各部分的名称
圆柱的表面积
圆柱的体积
圆柱的侧面积
圆柱的特征
圆 柱
知识梳理
圆柱和圆锥
圆柱的侧面积、表面积
圆柱和圆锥的特征
圆柱和圆锥的体积
S侧 = Ch
V柱= Sh
S表= S底×2+S侧
1
3
V锥= Sh
知识
方法
用转化、实验等方法探究圆柱、圆锥的体积。
知识梳理
底面
底面
高
侧面
圆柱的特征:
知识梳理
高
底面
侧面
顶点
圆锥的特征:
知识梳理
圆柱的侧面积=底面周长×高
底面
底面
高
底面周长
圆柱的表面积=底面积×2 + 侧面积
圆柱的表面积:
知识梳理
圆柱的体积:
V = S h
底面积
高
圆柱的体积
=
×
长方体的体积=底面积 × 高
知识梳理
圆锥的体积 = × 底面积×高
Ⅴ= sh
1
3
圆锥的体积是等底等高的圆柱体积的 。
圆锥的体积:
×
知识梳理
图形 特征 侧面积、
表面积公式 体积公式
圆柱
圆锥 -----
两个同样大小的
底面,一个侧面,
有无数条高。
一个底面,一个
侧面,一个顶点,
只能画一条高。
V柱=Sh
V锥= Sh
1
3
S侧=Ch
S表=S底×2+S侧
知识梳理
长方体、正方体体积公式的推导过程:
现实问题
数学问题
联想已有
知识经验
知识梳理
寻找方法
知识梳理
归纳结论
解决问题
解释应用
知识梳理
方法整理:
现实问题
怎样求圆柱形包装盒的体积?
数学问题
联想已有知识经验
归纳结论
解决问题、解释应用
产生新问题
怎样求圆柱体的体积?
推导圆面积公式时,是把圆转化成近似的长方形,推导圆柱体体积计算公式时,可否把它转化成长方体来研究呢?
猜想、验证、总结体积公式:V=Sh
运用公式求出圆柱体的体积,解决求冰淇淋包装盒的问题。
在解决问题的过程中产生新问题。
寻找方法
分一分,
切一切,
拼一拼。
知识梳理
圆柱的体积:
(60÷2)2×3.14×60
= 900 ×3.14×60
= 169560(立方厘米)
169560立方厘米=169.56立方分米
60厘米
60厘米
难点突破
李老师做一件冰雕作品,要将两个棱长为60厘米的正方体冰块分别雕成最大的圆柱和圆锥。它们的体积各是多少立方分米?
难点突破
169.56 ×
圆锥的体积:
1
3
答:圆柱和圆锥的体积分别是
169.56立方分米和56.52立方分米。
60厘米
60厘米
=56.52(立方分米)
李老师做一件冰雕作品,要将两个棱长为60厘米的正方体冰块分别雕成最大的圆柱和圆锥。它们的体积各是多少立方分米?
2.1米
10米
6米
(1)这个粮仓的占地面积有多大?
(2)它的容积是多少立方米?
(墙壁的厚度忽略不计。)
(1)(10÷2)2×3.14=78.5(平方米)
答:粮仓的占地面积是78.5平方米。
= 471+54.95
= 525.95(立方米)
答:它的容积是525.95立方米。
(2)78.5×6+78.5×2.1×
难点突破
圆柱的认识
圆 柱
圆柱的表面积
圆柱的侧面积
底面积
圆柱的体积
圆 锥
圆锥的认识
圆锥体积的计算
回顾整理
本课小结
3dm
8cm
6m
10dm
50.24cm2
4m
28.26dm2
12.56m2
226.08cm2
244.92dm2
113.04m2
251.2cm3
37.68m3
150.72m3
填一填。
随堂检测
一个圆柱形的水池,从里面量得底面直径是16米,深为1.5米。 它的容积是多少立方米?它的四周和底面抹有水泥,至少用了多少千克水泥?(每平方米用水泥10千克。)
水池的容积:
(16÷2)2×3.14×1.5
= 82 ×3.14×1.5
= 301.44(立方米)
答:水池的容积是301.44立方米。
水泥的重量:
(16÷2)2×3.14+16×3.14×1.5
= 82 ×3.14+50.24×1.5
= 276.32(平方米)
答:至少用了2763.2千克水泥。
276.32×10 = 2763.2(千克)
随堂检测
一根竹筒从里面量直径为4厘米,长为10厘米。把大米装至竹筒长的 处做米饭,如果每立方厘米大米约重3克,这根竹筒里的大米大约重多少克?
(只列式不计算。)
3
5
3×3.14×(4÷2)2×10×
3
5
随堂检测
孔庙大成殿前檐有10根石雕龙柱,高6米,直径为0.8米。已知每立方米石料约重2.7吨,这些柱子大约重多少吨?(只列式不计算。)
(0.8÷2)2×3.14×6×10×2.7
随堂检测
30cm
2m
结合圆柱和圆锥的知识,联系实际,展开想象的翅膀,看看你能提出什么问题,你能列出算式吗?
(1)圆柱的表面积是多少平方厘米?
(2)圆柱的体积是多少立方厘米?
(3)如果把它削成一个最大圆锥体,圆锥体的体积是多少立方厘米?
3.14×(30÷2)2 ×200
3.14×30×200+3.14×(30÷2)2 ×2
1
3
×3.14×(30÷2)2 ×200
随堂检测
随堂检测
如果每人每天刷牙要用2厘米长的牙膏,那么1个月(30)天要用多少立方厘米的牙膏?如果管口的直径减少1毫米,那么1个月(30)大约节省多少立方厘米的牙膏?(得数保留整数)
6mm=0.3cm
3.14 × (0.6 ÷ 2)2 × 2 × 30
=3.14 × 0.32 × 2 × 30
=16.956(cm2)
≈17 (cm2 )
答:1个月大约要用17cm2 的牙膏。
6-1=5(mm)5mm=0.5cm
3.14 × (0.5 ÷ 2)2 × 2 × 30
=3.14 × 0.252 × 2 × 30
=11.775(cm2)
≈12(cm2 )
17 – 12 = 5cm2
答:1个月大约节约5cm2 的牙膏。
作业布置
(1)做一个雨量器的外壳(无盖),至少需要多少平方厘米材料?(可以用计算器计算)
(2)储水瓶里一共接了多少毫升雨水?
空白演示
单击输入您的封面副标题
谢 谢 聆 听
