2021-2022学年华师大版七年级数学上册期末综合复习训练1 第5章相交线与平行线(Word版含解析)
文档属性
| 名称 | 2021-2022学年华师大版七年级数学上册期末综合复习训练1 第5章相交线与平行线(Word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 268.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 16:35:17 | ||
图片预览



文档简介
2021-2022学年华师大版七年级数学上册《第5章相交线与平行线》
期末综合复习训练1(附答案)
1.平面内有两两相交的4条直线,如果最多有m个交点,最少有n个交点,那么m+n=( )
A.9 B.8 C.7 D.6
2.下列四个选项的图形中,结论“∠1=∠2”一定成立的是( )
A.B.C.D.
3.下列语句中,正确的是( )
A.相等的角是对顶角 B.三个锐角的和一定大于直角
C.过一点,有且只有一条直线与已知直线垂直
D.如果∠1与∠2互余,∠1与∠3互余,那么一定有∠2=∠3
4.如图所示,在三角形ABC中,AC⊥BC,CD⊥AB,垂足分别是C,D,那么以下线段大小的比较必定成立的是( )
A.CD>AD B.AC<BC C.BC>BD D.CD<BD
5.如图,点P是直线l外的一点,点A、B、C在直线l上,且PB⊥l,垂足是B,PA⊥PC,则下列判断不正确的是( )
A.线段PB的长是点P到直线l的距离 B.PA、PB、PC三条线段中,PB最短
C.线段AC的长是点A到直线PC的距离 D.线段PC的长是点C到直线PA的距离
6.如图,下列各角与∠A是同位角的是( )
A.∠1 B.∠2 C.∠3 D.∠4
7.下列说法:
①在同一平面内,不相交的两条线段叫做平行线;②过一点,有且只有一条直线平行于已知直线;③两条平行直线被第三条直线所截,同位角相等;
④同旁内角相等,两直线平行.正确的个数有( )个.
A.1 B.2 C.3 D.4
8.下列说法正确的是( )
A.两点之间的距离是两点间的线段
B.与同一条直线垂直的两条直线也垂直
C.同一平面内,过一点有且只有一条直线与已知直线平行
D.同一平面内,过一点有且只有一条直线与已知直线垂直
9.如图所示,下列推理正确的是( )
A.∵∠1=∠4(已知)∴AB∥CD(内错角相等,两直线平行)
B.∵∠2=∠3(已知)∴AE∥DF(内错角相等,两直线平行)
C.∵∠1=∠3(已知)∴AB∥DF(内错角相等,两直线平行)
D.∵∠2=∠3(已知)∴AE∥DC(内错角相等,两直线平行)
10.将一把直尺和一块含30°角的直角三角板按如图所示方式摆放,其中∠CBD=90°,∠BDC=30°,若∠1=78°,则∠2的度数为( )
A.19° B.18° C.17° D.16°
11.将一副三角板按如图放置,则下列结论:①∠1=∠3;②∠CAD+∠2=180°;③若∠1=45°,则有BC∥AD;④如果∠2=30°,必有∠4=∠C,其中正确的有( )
A.①②③ B.①②④ C.③④ D.①②③④
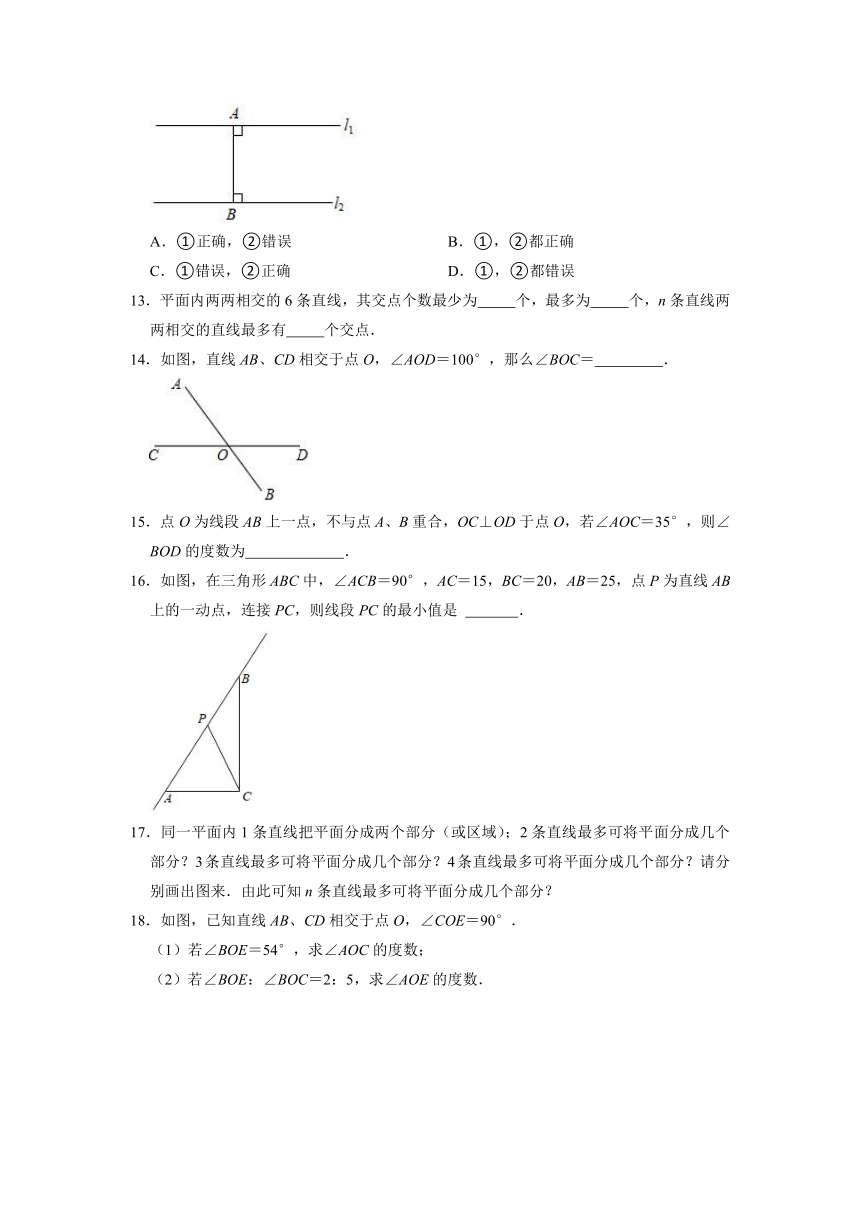
12.如图,点A,B分别在直线l1,l2上,且l1∥l2,AB⊥l1.有两种说法:
①线段AB的长是A,B两点之间的距离;
②线段AB的长是平行线l1,l2之间的距离.
关于这两种说法,正确的是( )
A.①正确,②错误 B.①,②都正确
C.①错误,②正确 D.①,②都错误
13.平面内两两相交的6条直线,其交点个数最少为 个,最多为 个,n条直线两两相交的直线最多有 个交点.
14.如图,直线AB、CD相交于点O,∠AOD=100°,那么∠BOC= .
15.点O为线段AB上一点,不与点A、B重合,OC⊥OD于点O,若∠AOC=35°,则∠BOD的度数为 .
16.如图,在三角形ABC中,∠ACB=90°,AC=15,BC=20,AB=25,点P为直线AB上的一动点,连接PC,则线段PC的最小值是 .
17.同一平面内1条直线把平面分成两个部分(或区域);2条直线最多可将平面分成几个部分?3条直线最多可将平面分成几个部分?4条直线最多可将平面分成几个部分?请分别画出图来.由此可知n条直线最多可将平面分成几个部分?
18.如图,已知直线AB、CD相交于点O,∠COE=90°.
(1)若∠BOE=54°,求∠AOC的度数;
(2)若∠BOE:∠BOC=2:5,求∠AOE的度数.
19.已知:如图,直线l和l外一点A.求作:直线AE,使得AE⊥l于点E.
20.如图所示,在△ABC中,AC=5,BC=6,BC边上高AD=4,若点P在边AC上(不含端点)移动,求BP最短时的值.
21.在三角形ABC中,回答相应的问题(要求自己画出三角形ABC):
已知:BC⊥AC,CB=8cm,AC=6cm,AB=10cm,那么点B到AC的距离是 ;点A到BC的距离是 ;点C到AB的距离是 .
22.如图所示,已知∠1=115°,∠2=65°,∠3=100°.
(1)图中所有角中(包含没有标数字的角),共有几对内错角?
(2)求∠4的大小.
23.(1)补全下面图形,使之成为长方体ABCD﹣A1B1C1D1的直观图;
(2)写出既与棱AB异面又与棱DD1平行的棱: ;
(3)长方体ABCD﹣A1B1C1D1的长、宽、高的比是3:2:1,它的所有棱长和是24厘米,那么这个长方体的体积是 立方厘米.
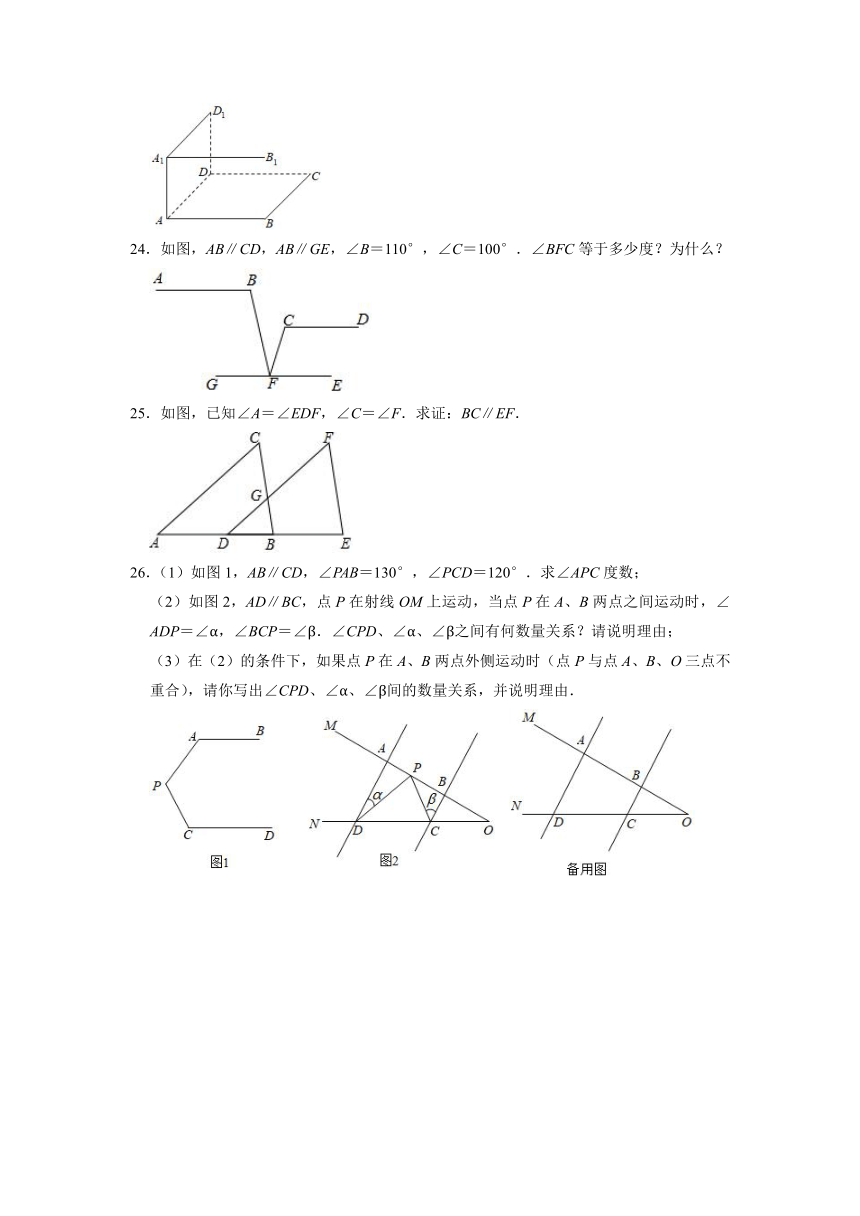
24.如图,AB∥CD,AB∥GE,∠B=110°,∠C=100°.∠BFC等于多少度?为什么?
25.如图,已知∠A=∠EDF,∠C=∠F.求证:BC∥EF.
26.(1)如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC度数;
(2)如图2,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.∠CPD、∠α、∠β之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你写出∠CPD、∠α、∠β间的数量关系,并说明理由.
参考答案
1.解:如图所示:
4条直线两两相交,有3种情况:4条直线经过同一点,有一个交点;3条直线经过同一点,被第4条直线所截,有4个交点;4条直线不经过同一点,有6个交点.
故平面内两两相交的4条直线,最多有6个交点,最少有1个交点;即m=6,n=1,则m+n=7.
故选:C.
2.解:A、∠1与∠2是邻补角,和为180°,不一定相等,不符合题意;
B、∠2是三角形的外角,∠2>∠1,不符合题意;
C、∠1与∠2是对顶角,相等,符合题意;
D、∠1与∠2是同旁内角,不一定相等,不符合题意;
故选:C.
3.解:A、相等的角不一定是对顶角,原说法错误,故此选项不符合题意;
B、三个锐角的和不一定大于直角,如三个锐角分别是10°、20°、30°,它们的和就不大于直角,原说法错误,故此选项不符合题意;
C、在平面内,过一点有且只有一条直线与已知直线垂直,原说法错误,故此选项不符合题意;
D、如果∠1与∠2互余,∠1与∠3互余,那么一定有∠2=∠3,根据是同角的余角相等,原说法正确,故此选项符合题意.
故选:D.
4.解:A、CD与AD互相垂直,没有明确的大小关系,故本选项不符合题意;
B、AC与BC互相垂直,没有明确的大小关系,故本选项不符合题意;
C、BD是从直线CD外一点B所作的垂线段,根据垂线段最短定理,BC>BD,故本选项符合题意;
D、CD与BD互相垂直,没有明确的大小关系,故本选项不符合题意;
故选:C.
5.解:A、线段PB的长度叫做点P到直线l的距离,原说法正确,故此选项不符合题意;
B、PA、PB、PC三条线段中,依据垂线段最短可知PB最短,原说法正确,故此选项不符合题意;
C、线段PA的长度叫做点A到直线PC的距离,原说法不正确,故此选项符合题意;
D、线段PC的长是点C到直线PA的距离,原说法正确,故此选项不符合题意;
故选:C.
6.解:直线AB,DE被直线AC所截而成的角中,∠A与∠3在两直线的同侧,并且在截线的同旁,所以∠A的同位角是∠3.
故选:C.
7.解:①在同一平面内,不相交的两条直线叫做平行线,故原命题错误;
②过直线外一点,有且只有一条直线平行于已知直线,故原命题错误;
③两条平行直线被第三条直线所截,同位角相等,故原命题正确;
④同旁内角互补,两直线平行,故原命题错误.
故选:A.
8.解:A、两点之间的距离是指两点间的线段长度,而不是线段本身,错误;
B、在同一平面内,与同一条直线垂直的两条直线平行,错误;
C、同一平面内,过直线外一点有且只有一条直线与已知直线平行,应强调“直线外”,错误;
D、这是垂线的性质,正确.
故选:D.
9.解:A、错误.∠1和∠4不是内错角,推不出AB∥CD;
B、正确.内错角相等,两直线平行;
C、错误.∠1和∠3不是内错角,推不出AB∥DF;
D、错误.由∠2=∠3推出AE∥DF.
故选:B.
10.解:∵∠CBD=90°,∠1=78°,
∴∠DBE=180°﹣∠CBD﹣∠1=180°﹣90°﹣78°=12°,
∵直尺的两边平行,即EA∥GH,
∴∠BDF=∠DBE=12°,
∵∠BDC=30°,
∴∠2=∠BDC﹣∠BDF=30°﹣12°=18°,
故选:B.
11.解:∵∠1+∠2=90°,∠3+∠2=90°,
∴∠1=∠3,
故①正确;
∵∠CAD+∠2=∠1+∠2+∠3+∠2=90°+90°=180°,
故②正确;
∵∠1=45°,
∴∠3=∠B=45°,
∴BC∥AD.
故③正确;
∵∠2=30°,
∴∠1=∠E=60°,
∴AC∥DE,
∴∠4=∠C,
故④正确.
故选:D.
12.解:①线段AB的长是A,B两点之间的距离,原说法正确;
②线段AB的长是平行线l1,l2之间的距离,原说法正确.
故选:B.
13.解:根据题意可得:6条直线相交于一点时交点最少,此时交点为1个;
若平面内有相交的2条直线,则最多有1个交点;(即:1==1);
若平面内有两两相交的3条直线,则最多有3个交点;(即:1+2==3);
若平面内有两两相交的4条直线,则最多有6个交点;(即:1+2+3==6);
若平面内有两两相交的5条直线,则最多有10个交点;(即:1+2+3+4==10);
则平面内两两相交的6条直线,其交点个数最多有15个交点;(即1+2+3+4+5==15);
若平面内有n条直线两两相交,则最多有个交点;
故答案为:1,15,.
14.解:∵∠AOD=100°,∠BOC与∠AOD是对顶角,
∴∠BOC=∠AOD=100°,
故答案为:100°.
15.解:当OC和OD在AB同一侧时,如图:
∵OC⊥OD,
∴∠COD=90°,
∴∠AOC+∠BOD=90°,
∵∠AOC=35°,
∴∠BOD=90°﹣∠AOC=90°﹣35°=55°,
当OC和OD在AB同异侧时,如图:
∵OC⊥OD,
∴∠COD=90°,
∵∠AOC=35°,
∴∠AOD=55°,
∴∠BOD=180°﹣∠AOD=180°﹣55°=125°.
∴∠BOD的度数为55°或125°.
故答案为:55°或125°.
16.解:在Rt△ABC中,∠ACB=90°,AC=15,BC=20,AB=25,
∵当PC⊥AB时,PC的值最小,
此时:△ABC的面积= AB PC= AC BC,
∴25PC=15×20,
∴PC=12,
故答案为:12.
17.解:2条直线最多可将平面分成4个部分,如图:;
三条直线最多分成可将平面分成7个部分,如图:;
四条直线最多分成可将平面分成11个部分,如图:;
n条直线最多分成可将平面分成2+2+3+4+…+n=个部分.
18.解:(1)∵∠COE=90°,
∴∠DOE=90°,
∵∠BOE=54°,
∴∠BOD=∠DOE﹣∠BOE=90°﹣54°=36°,
∴∠AOC=∠BOD=36°;
(2)设∠BOE=2x,∠BOC=5x,则∠COE=3x,
∵∠COE=90°,
∴3x=90°,
解得x=30°,
∴∠BOE=2×30°=60°,
∴∠AOE=180°﹣∠BOE=180°﹣60°=120°.
19.解:已知:直线l和l外一点A.
求作:直线l的垂线AE,垂足为点E.
作法:(1)任意取一点K,使K与A在直线l的两旁;
(2)以点A为圆心,AK长为半径作弧,交l于点D和M.
(3)分别以D和M为圆心,大于DM的长为半径作弧,两弧交于点F.
(4)连接AF,交直线l为点E.
所以直线AE就是所求作的垂线.
20.解:根据垂线段最短可知,当BP⊥AC时,BP最短,
∵S△ABC=×BC×AD=×AC×BP,
∴6×4=5BP,
∴PB=,
即BP最短时的值为:.
21.解:△ABC如图:
过点C作CD⊥AB于点D,则线段CD的长即为点C到AB的距离,
∵BC⊥AC,CB=8cm,AB=10cm,AC=6cm,
∴CD=6×8÷10=4.8(cm),
点A到BC的距离是6cm,
点B到AC的距离是8cm.
故答案为:8cm,6cm,4.8cm.
22.解:如图所示:
(1)直线c和d被直线b所截,有两对内错角,
即∠2和∠6,∠5和∠7,
同理还有六对内错角,
共有8对内错角;
(2)∵∠2+∠5=180°,∠2=65°,
∴∠5=180°﹣65°=115°,
∵∠1=115°,
∴∠1=∠5,
∴a∥b,
∴∠3=∠6,
又∵∠3=100°,
∴∠6=100°,
∴∠4=∠6=100°.
23.解:(1)画出图形如图:
(2)既与棱AB异面又与棱DD1平行的棱是CC1;
(3)24÷4=6(厘米),
6×=3(厘米);
6×=2(厘米);
6×=1(厘米).
3×2×1=6(立方厘米).
所以长方体的体积是6立方厘米.
故答案为:CC1,6.
24.解:∠BFC等于30度,理由如下:
∵AB∥GE,
∴∠B+∠BFG=180°,
∵∠B=110°,
∴∠BFG=180°﹣110°=70°,
∵AB∥CD,AB∥GE,
∴CD∥GE,
∴∠C+∠CFE=180°,
∵∠C=100°.
∴∠CFE=180°﹣100°=80°,
∴∠BFC=180°﹣∠BFG﹣∠CFE=180°﹣70°﹣80°=30°.
25.证明:∵∠A=∠EDF(已知),
∴AC∥DF(同位角相等,两直线平行),
∴∠C=∠CGF(两直线平行,内错角相等).
又∵∠C=∠F(已知),
∴∠CGF=∠F(等量代换),
∴BC∥EF(内错角相等,两直线平行).
26.解:(1)如图1,过点P作GH∥AB.
∴∠BAP+∠APH=180°.
∴∠APH=180°﹣∠BAP=180°﹣130°=50°
∵AB∥CD,GH∥AB.
∴CD∥GH.
∴∠PCD+∠HPC=180°.
∴∠HPC=180°﹣∠PCD=180°﹣120°=60°.
∴∠APC=∠HPC+∠APH=60°+50°=110°.
(2)如图2,过点P作EF∥AD.
∴∠ADP=∠DPF,即∠α=∠DPF.
∵EF∥AD,AD∥BC,
∴EF∥BC.
∴∠FPC=∠PCB,即∠FPC=∠β.
∴∠CPD=∠DPF+∠CPF=∠α+∠β.
∴∠CPD=∠α+∠β.
(3)当P在A的左侧,如图3.
∵AD∥BC,
∴∠DKC=∠BCP=∠β.
又∵∠DKC=∠CPD+∠ADP,
∴∠β=∠CPD+∠α,即∠CPD=∠β﹣∠α.
当P在B的右侧,如图4.
∵AD∥BC,
∴∠ADP=∠DQC=∠α.
又∵∠DQC=∠CPD+∠BCP,
∴∠α=∠CPD+∠β.
∴∠CPD=∠α﹣∠β.
期末综合复习训练1(附答案)
1.平面内有两两相交的4条直线,如果最多有m个交点,最少有n个交点,那么m+n=( )
A.9 B.8 C.7 D.6
2.下列四个选项的图形中,结论“∠1=∠2”一定成立的是( )
A.B.C.D.
3.下列语句中,正确的是( )
A.相等的角是对顶角 B.三个锐角的和一定大于直角
C.过一点,有且只有一条直线与已知直线垂直
D.如果∠1与∠2互余,∠1与∠3互余,那么一定有∠2=∠3
4.如图所示,在三角形ABC中,AC⊥BC,CD⊥AB,垂足分别是C,D,那么以下线段大小的比较必定成立的是( )
A.CD>AD B.AC<BC C.BC>BD D.CD<BD
5.如图,点P是直线l外的一点,点A、B、C在直线l上,且PB⊥l,垂足是B,PA⊥PC,则下列判断不正确的是( )
A.线段PB的长是点P到直线l的距离 B.PA、PB、PC三条线段中,PB最短
C.线段AC的长是点A到直线PC的距离 D.线段PC的长是点C到直线PA的距离
6.如图,下列各角与∠A是同位角的是( )
A.∠1 B.∠2 C.∠3 D.∠4
7.下列说法:
①在同一平面内,不相交的两条线段叫做平行线;②过一点,有且只有一条直线平行于已知直线;③两条平行直线被第三条直线所截,同位角相等;
④同旁内角相等,两直线平行.正确的个数有( )个.
A.1 B.2 C.3 D.4
8.下列说法正确的是( )
A.两点之间的距离是两点间的线段
B.与同一条直线垂直的两条直线也垂直
C.同一平面内,过一点有且只有一条直线与已知直线平行
D.同一平面内,过一点有且只有一条直线与已知直线垂直
9.如图所示,下列推理正确的是( )
A.∵∠1=∠4(已知)∴AB∥CD(内错角相等,两直线平行)
B.∵∠2=∠3(已知)∴AE∥DF(内错角相等,两直线平行)
C.∵∠1=∠3(已知)∴AB∥DF(内错角相等,两直线平行)
D.∵∠2=∠3(已知)∴AE∥DC(内错角相等,两直线平行)
10.将一把直尺和一块含30°角的直角三角板按如图所示方式摆放,其中∠CBD=90°,∠BDC=30°,若∠1=78°,则∠2的度数为( )
A.19° B.18° C.17° D.16°
11.将一副三角板按如图放置,则下列结论:①∠1=∠3;②∠CAD+∠2=180°;③若∠1=45°,则有BC∥AD;④如果∠2=30°,必有∠4=∠C,其中正确的有( )
A.①②③ B.①②④ C.③④ D.①②③④
12.如图,点A,B分别在直线l1,l2上,且l1∥l2,AB⊥l1.有两种说法:
①线段AB的长是A,B两点之间的距离;
②线段AB的长是平行线l1,l2之间的距离.
关于这两种说法,正确的是( )
A.①正确,②错误 B.①,②都正确
C.①错误,②正确 D.①,②都错误
13.平面内两两相交的6条直线,其交点个数最少为 个,最多为 个,n条直线两两相交的直线最多有 个交点.
14.如图,直线AB、CD相交于点O,∠AOD=100°,那么∠BOC= .
15.点O为线段AB上一点,不与点A、B重合,OC⊥OD于点O,若∠AOC=35°,则∠BOD的度数为 .
16.如图,在三角形ABC中,∠ACB=90°,AC=15,BC=20,AB=25,点P为直线AB上的一动点,连接PC,则线段PC的最小值是 .
17.同一平面内1条直线把平面分成两个部分(或区域);2条直线最多可将平面分成几个部分?3条直线最多可将平面分成几个部分?4条直线最多可将平面分成几个部分?请分别画出图来.由此可知n条直线最多可将平面分成几个部分?
18.如图,已知直线AB、CD相交于点O,∠COE=90°.
(1)若∠BOE=54°,求∠AOC的度数;
(2)若∠BOE:∠BOC=2:5,求∠AOE的度数.
19.已知:如图,直线l和l外一点A.求作:直线AE,使得AE⊥l于点E.
20.如图所示,在△ABC中,AC=5,BC=6,BC边上高AD=4,若点P在边AC上(不含端点)移动,求BP最短时的值.
21.在三角形ABC中,回答相应的问题(要求自己画出三角形ABC):
已知:BC⊥AC,CB=8cm,AC=6cm,AB=10cm,那么点B到AC的距离是 ;点A到BC的距离是 ;点C到AB的距离是 .
22.如图所示,已知∠1=115°,∠2=65°,∠3=100°.
(1)图中所有角中(包含没有标数字的角),共有几对内错角?
(2)求∠4的大小.
23.(1)补全下面图形,使之成为长方体ABCD﹣A1B1C1D1的直观图;
(2)写出既与棱AB异面又与棱DD1平行的棱: ;
(3)长方体ABCD﹣A1B1C1D1的长、宽、高的比是3:2:1,它的所有棱长和是24厘米,那么这个长方体的体积是 立方厘米.
24.如图,AB∥CD,AB∥GE,∠B=110°,∠C=100°.∠BFC等于多少度?为什么?
25.如图,已知∠A=∠EDF,∠C=∠F.求证:BC∥EF.
26.(1)如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC度数;
(2)如图2,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.∠CPD、∠α、∠β之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你写出∠CPD、∠α、∠β间的数量关系,并说明理由.
参考答案
1.解:如图所示:
4条直线两两相交,有3种情况:4条直线经过同一点,有一个交点;3条直线经过同一点,被第4条直线所截,有4个交点;4条直线不经过同一点,有6个交点.
故平面内两两相交的4条直线,最多有6个交点,最少有1个交点;即m=6,n=1,则m+n=7.
故选:C.
2.解:A、∠1与∠2是邻补角,和为180°,不一定相等,不符合题意;
B、∠2是三角形的外角,∠2>∠1,不符合题意;
C、∠1与∠2是对顶角,相等,符合题意;
D、∠1与∠2是同旁内角,不一定相等,不符合题意;
故选:C.
3.解:A、相等的角不一定是对顶角,原说法错误,故此选项不符合题意;
B、三个锐角的和不一定大于直角,如三个锐角分别是10°、20°、30°,它们的和就不大于直角,原说法错误,故此选项不符合题意;
C、在平面内,过一点有且只有一条直线与已知直线垂直,原说法错误,故此选项不符合题意;
D、如果∠1与∠2互余,∠1与∠3互余,那么一定有∠2=∠3,根据是同角的余角相等,原说法正确,故此选项符合题意.
故选:D.
4.解:A、CD与AD互相垂直,没有明确的大小关系,故本选项不符合题意;
B、AC与BC互相垂直,没有明确的大小关系,故本选项不符合题意;
C、BD是从直线CD外一点B所作的垂线段,根据垂线段最短定理,BC>BD,故本选项符合题意;
D、CD与BD互相垂直,没有明确的大小关系,故本选项不符合题意;
故选:C.
5.解:A、线段PB的长度叫做点P到直线l的距离,原说法正确,故此选项不符合题意;
B、PA、PB、PC三条线段中,依据垂线段最短可知PB最短,原说法正确,故此选项不符合题意;
C、线段PA的长度叫做点A到直线PC的距离,原说法不正确,故此选项符合题意;
D、线段PC的长是点C到直线PA的距离,原说法正确,故此选项不符合题意;
故选:C.
6.解:直线AB,DE被直线AC所截而成的角中,∠A与∠3在两直线的同侧,并且在截线的同旁,所以∠A的同位角是∠3.
故选:C.
7.解:①在同一平面内,不相交的两条直线叫做平行线,故原命题错误;
②过直线外一点,有且只有一条直线平行于已知直线,故原命题错误;
③两条平行直线被第三条直线所截,同位角相等,故原命题正确;
④同旁内角互补,两直线平行,故原命题错误.
故选:A.
8.解:A、两点之间的距离是指两点间的线段长度,而不是线段本身,错误;
B、在同一平面内,与同一条直线垂直的两条直线平行,错误;
C、同一平面内,过直线外一点有且只有一条直线与已知直线平行,应强调“直线外”,错误;
D、这是垂线的性质,正确.
故选:D.
9.解:A、错误.∠1和∠4不是内错角,推不出AB∥CD;
B、正确.内错角相等,两直线平行;
C、错误.∠1和∠3不是内错角,推不出AB∥DF;
D、错误.由∠2=∠3推出AE∥DF.
故选:B.
10.解:∵∠CBD=90°,∠1=78°,
∴∠DBE=180°﹣∠CBD﹣∠1=180°﹣90°﹣78°=12°,
∵直尺的两边平行,即EA∥GH,
∴∠BDF=∠DBE=12°,
∵∠BDC=30°,
∴∠2=∠BDC﹣∠BDF=30°﹣12°=18°,
故选:B.
11.解:∵∠1+∠2=90°,∠3+∠2=90°,
∴∠1=∠3,
故①正确;
∵∠CAD+∠2=∠1+∠2+∠3+∠2=90°+90°=180°,
故②正确;
∵∠1=45°,
∴∠3=∠B=45°,
∴BC∥AD.
故③正确;
∵∠2=30°,
∴∠1=∠E=60°,
∴AC∥DE,
∴∠4=∠C,
故④正确.
故选:D.
12.解:①线段AB的长是A,B两点之间的距离,原说法正确;
②线段AB的长是平行线l1,l2之间的距离,原说法正确.
故选:B.
13.解:根据题意可得:6条直线相交于一点时交点最少,此时交点为1个;
若平面内有相交的2条直线,则最多有1个交点;(即:1==1);
若平面内有两两相交的3条直线,则最多有3个交点;(即:1+2==3);
若平面内有两两相交的4条直线,则最多有6个交点;(即:1+2+3==6);
若平面内有两两相交的5条直线,则最多有10个交点;(即:1+2+3+4==10);
则平面内两两相交的6条直线,其交点个数最多有15个交点;(即1+2+3+4+5==15);
若平面内有n条直线两两相交,则最多有个交点;
故答案为:1,15,.
14.解:∵∠AOD=100°,∠BOC与∠AOD是对顶角,
∴∠BOC=∠AOD=100°,
故答案为:100°.
15.解:当OC和OD在AB同一侧时,如图:
∵OC⊥OD,
∴∠COD=90°,
∴∠AOC+∠BOD=90°,
∵∠AOC=35°,
∴∠BOD=90°﹣∠AOC=90°﹣35°=55°,
当OC和OD在AB同异侧时,如图:
∵OC⊥OD,
∴∠COD=90°,
∵∠AOC=35°,
∴∠AOD=55°,
∴∠BOD=180°﹣∠AOD=180°﹣55°=125°.
∴∠BOD的度数为55°或125°.
故答案为:55°或125°.
16.解:在Rt△ABC中,∠ACB=90°,AC=15,BC=20,AB=25,
∵当PC⊥AB时,PC的值最小,
此时:△ABC的面积= AB PC= AC BC,
∴25PC=15×20,
∴PC=12,
故答案为:12.
17.解:2条直线最多可将平面分成4个部分,如图:;
三条直线最多分成可将平面分成7个部分,如图:;
四条直线最多分成可将平面分成11个部分,如图:;
n条直线最多分成可将平面分成2+2+3+4+…+n=个部分.
18.解:(1)∵∠COE=90°,
∴∠DOE=90°,
∵∠BOE=54°,
∴∠BOD=∠DOE﹣∠BOE=90°﹣54°=36°,
∴∠AOC=∠BOD=36°;
(2)设∠BOE=2x,∠BOC=5x,则∠COE=3x,
∵∠COE=90°,
∴3x=90°,
解得x=30°,
∴∠BOE=2×30°=60°,
∴∠AOE=180°﹣∠BOE=180°﹣60°=120°.
19.解:已知:直线l和l外一点A.
求作:直线l的垂线AE,垂足为点E.
作法:(1)任意取一点K,使K与A在直线l的两旁;
(2)以点A为圆心,AK长为半径作弧,交l于点D和M.
(3)分别以D和M为圆心,大于DM的长为半径作弧,两弧交于点F.
(4)连接AF,交直线l为点E.
所以直线AE就是所求作的垂线.
20.解:根据垂线段最短可知,当BP⊥AC时,BP最短,
∵S△ABC=×BC×AD=×AC×BP,
∴6×4=5BP,
∴PB=,
即BP最短时的值为:.
21.解:△ABC如图:
过点C作CD⊥AB于点D,则线段CD的长即为点C到AB的距离,
∵BC⊥AC,CB=8cm,AB=10cm,AC=6cm,
∴CD=6×8÷10=4.8(cm),
点A到BC的距离是6cm,
点B到AC的距离是8cm.
故答案为:8cm,6cm,4.8cm.
22.解:如图所示:
(1)直线c和d被直线b所截,有两对内错角,
即∠2和∠6,∠5和∠7,
同理还有六对内错角,
共有8对内错角;
(2)∵∠2+∠5=180°,∠2=65°,
∴∠5=180°﹣65°=115°,
∵∠1=115°,
∴∠1=∠5,
∴a∥b,
∴∠3=∠6,
又∵∠3=100°,
∴∠6=100°,
∴∠4=∠6=100°.
23.解:(1)画出图形如图:
(2)既与棱AB异面又与棱DD1平行的棱是CC1;
(3)24÷4=6(厘米),
6×=3(厘米);
6×=2(厘米);
6×=1(厘米).
3×2×1=6(立方厘米).
所以长方体的体积是6立方厘米.
故答案为:CC1,6.
24.解:∠BFC等于30度,理由如下:
∵AB∥GE,
∴∠B+∠BFG=180°,
∵∠B=110°,
∴∠BFG=180°﹣110°=70°,
∵AB∥CD,AB∥GE,
∴CD∥GE,
∴∠C+∠CFE=180°,
∵∠C=100°.
∴∠CFE=180°﹣100°=80°,
∴∠BFC=180°﹣∠BFG﹣∠CFE=180°﹣70°﹣80°=30°.
25.证明:∵∠A=∠EDF(已知),
∴AC∥DF(同位角相等,两直线平行),
∴∠C=∠CGF(两直线平行,内错角相等).
又∵∠C=∠F(已知),
∴∠CGF=∠F(等量代换),
∴BC∥EF(内错角相等,两直线平行).
26.解:(1)如图1,过点P作GH∥AB.
∴∠BAP+∠APH=180°.
∴∠APH=180°﹣∠BAP=180°﹣130°=50°
∵AB∥CD,GH∥AB.
∴CD∥GH.
∴∠PCD+∠HPC=180°.
∴∠HPC=180°﹣∠PCD=180°﹣120°=60°.
∴∠APC=∠HPC+∠APH=60°+50°=110°.
(2)如图2,过点P作EF∥AD.
∴∠ADP=∠DPF,即∠α=∠DPF.
∵EF∥AD,AD∥BC,
∴EF∥BC.
∴∠FPC=∠PCB,即∠FPC=∠β.
∴∠CPD=∠DPF+∠CPF=∠α+∠β.
∴∠CPD=∠α+∠β.
(3)当P在A的左侧,如图3.
∵AD∥BC,
∴∠DKC=∠BCP=∠β.
又∵∠DKC=∠CPD+∠ADP,
∴∠β=∠CPD+∠α,即∠CPD=∠β﹣∠α.
当P在B的右侧,如图4.
∵AD∥BC,
∴∠ADP=∠DQC=∠α.
又∵∠DQC=∠CPD+∠BCP,
∴∠α=∠CPD+∠β.
∴∠CPD=∠α﹣∠β.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
