沪科版数学七年级上册 1.6 有理数的乘方(1) (共13张ppt)
文档属性
| 名称 | 沪科版数学七年级上册 1.6 有理数的乘方(1) (共13张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 895.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-25 07:29:06 | ||
图片预览




文档简介
(共13张PPT)
棋盘上的学问
古时候,在某个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋,为了对聪明的大臣表示感谢,国王答
应满足这个大臣的一个要求。大
臣说:“就在这个棋盘上放一些米
粒吧。第1格放1粒,第2格放2粒,
第3格放4粒,然后是8粒、16粒、
32粒、……一直到第64格。”“你真
傻! 就要这么一些米粒?!”国王哈
哈大笑。大臣说:“就怕你的国库
里没有这么多米!”
你认为国王的国库里有这么多米吗?
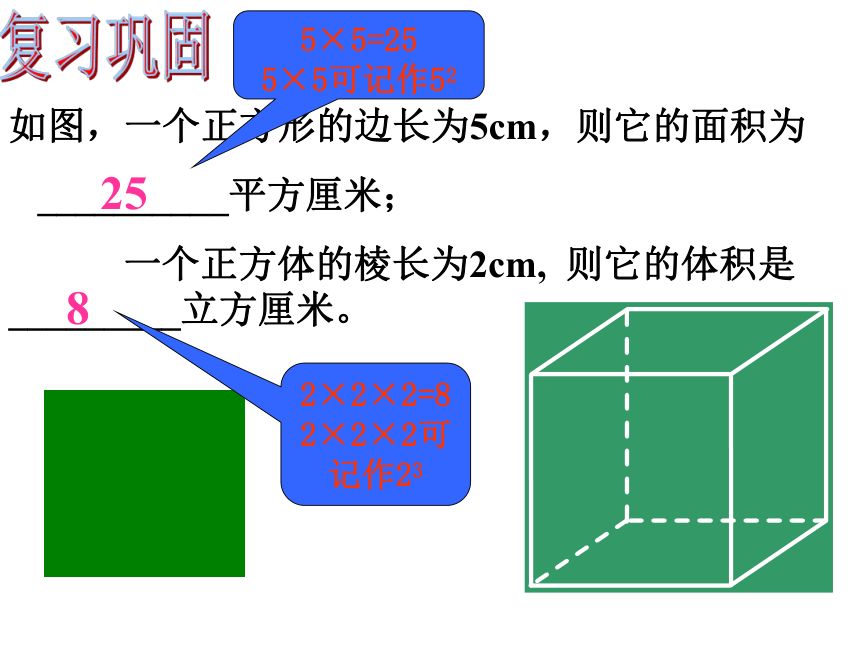
如图,一个正方形的边长为5cm,则它的面积为
__________平方厘米;
一个正方体的棱长为2cm, 则它的体积是_________立方厘米。
8
25
5×5=25
5×5可记作52
2×2×2=8
2×2×2可记作23
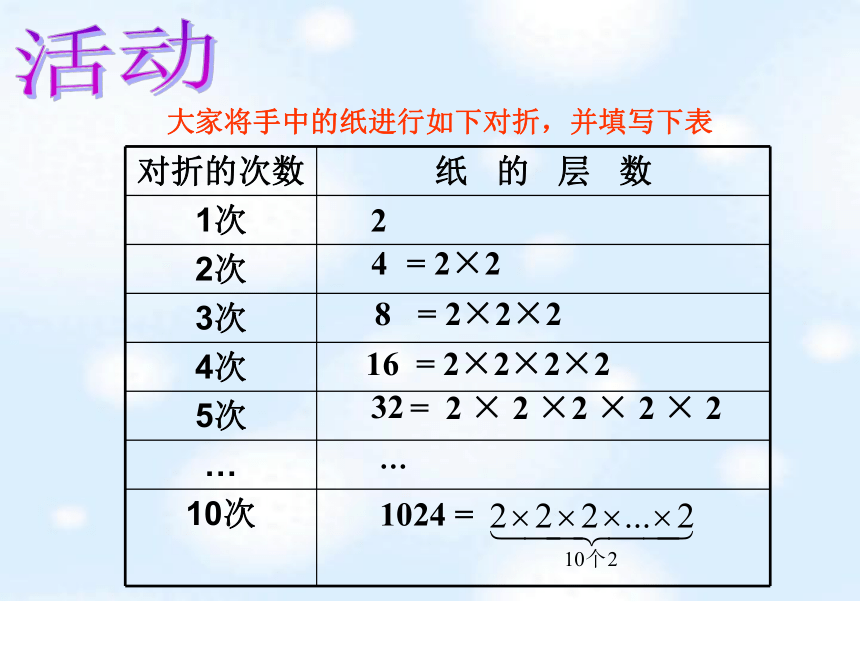
大家将手中的纸进行如下对折,并填写下表
对折的次数 纸 的 层 数
1次
2次
3次
4次
5次
…
10次
= 2 × 2 ×2 × 2 × 2
= 2×2×2×2
= 2×2×2
= 2×2
2
4
8
16
32
1024 =
…
对折100次裁成的张数,可用算式
计算,在这个积中有100个2相乘。这么长的算式有简单的记法吗?
边长为 的正方形的面积可记为:
那么4个 相乘可记为:
棱长为 的正方体的体积可记为:
个 相乘又可记为:
2
a
a
a
=
●
个相同的因数 相乘,即
我们把它记作 ;
即
这种求 个 的积的运算,叫做乘方。
乘方的结果叫做幂。
幂
指数
因数的个数
底数
因数
相同因数
(1次方可省略不写,2次方又叫平方,3次方又叫立方。)
特别规定:
7
7
7
底数
指数
-3
10
-3
-3
10
注:当底数是分数或负数时一定要注意写书方法,要将底数括在括号内。
温馨提示
思考:例1的两个幂,底数都是负数,为什么这两个幂一个是正数而另一个是负数呢?是由什么数来确定它们的正负呢?
当底数是负数时,幂的正负由指数确定,指数是偶数时,幂是正数;指数是奇数时,幂是负数。
如果幂的底数正数,那么这个幂有可能是负数吗?
不可能!正数的任何次幂是都正数
例1:计算
乘方运算的法则:
非零有理数的乘方,将其绝对值乘方,
结果的符号规律是:正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数。
0的正数次方是0,0的零次方没有意义
(1)(-1.5)2;(2)4×(-2)3
(3)-(-2)4;(4)(-2)3×(-2)2
3.计算(先确定符号,再算结果):
课后练习(P41):
1
2
4=
2×2
8=2 ×2 ×2
16= 2 ×2 ×2 ×2
……
=21
=22
=23
=24
第64格
=263
=18446744073709551616
1+2+4+8+16+…+18446744073709551616=______
第1格
第2格
第3格
第4格
第5格
注:一粒米的物理重量约为0.025克 ,1亿粒大米约0.025X100000000=2500000克 2500千克 即2.5吨
通过这节课的学习,我学会了……
1. 乘方概念、及表示方法。
2.乘方的运算法则。
“乘方”精神:虽然是简简单单的重复,但结果却是惊人的。做人也要这样,脚踏实地,一步一个脚印,成功也会令你惊喜的。
今日作业:P43习题1.6 第1题
棋盘上的学问
古时候,在某个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋,为了对聪明的大臣表示感谢,国王答
应满足这个大臣的一个要求。大
臣说:“就在这个棋盘上放一些米
粒吧。第1格放1粒,第2格放2粒,
第3格放4粒,然后是8粒、16粒、
32粒、……一直到第64格。”“你真
傻! 就要这么一些米粒?!”国王哈
哈大笑。大臣说:“就怕你的国库
里没有这么多米!”
你认为国王的国库里有这么多米吗?
如图,一个正方形的边长为5cm,则它的面积为
__________平方厘米;
一个正方体的棱长为2cm, 则它的体积是_________立方厘米。
8
25
5×5=25
5×5可记作52
2×2×2=8
2×2×2可记作23
大家将手中的纸进行如下对折,并填写下表
对折的次数 纸 的 层 数
1次
2次
3次
4次
5次
…
10次
= 2 × 2 ×2 × 2 × 2
= 2×2×2×2
= 2×2×2
= 2×2
2
4
8
16
32
1024 =
…
对折100次裁成的张数,可用算式
计算,在这个积中有100个2相乘。这么长的算式有简单的记法吗?
边长为 的正方形的面积可记为:
那么4个 相乘可记为:
棱长为 的正方体的体积可记为:
个 相乘又可记为:
2
a
a
a
=
●
个相同的因数 相乘,即
我们把它记作 ;
即
这种求 个 的积的运算,叫做乘方。
乘方的结果叫做幂。
幂
指数
因数的个数
底数
因数
相同因数
(1次方可省略不写,2次方又叫平方,3次方又叫立方。)
特别规定:
7
7
7
底数
指数
-3
10
-3
-3
10
注:当底数是分数或负数时一定要注意写书方法,要将底数括在括号内。
温馨提示
思考:例1的两个幂,底数都是负数,为什么这两个幂一个是正数而另一个是负数呢?是由什么数来确定它们的正负呢?
当底数是负数时,幂的正负由指数确定,指数是偶数时,幂是正数;指数是奇数时,幂是负数。
如果幂的底数正数,那么这个幂有可能是负数吗?
不可能!正数的任何次幂是都正数
例1:计算
乘方运算的法则:
非零有理数的乘方,将其绝对值乘方,
结果的符号规律是:正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数。
0的正数次方是0,0的零次方没有意义
(1)(-1.5)2;(2)4×(-2)3
(3)-(-2)4;(4)(-2)3×(-2)2
3.计算(先确定符号,再算结果):
课后练习(P41):
1
2
4=
2×2
8=2 ×2 ×2
16= 2 ×2 ×2 ×2
……
=21
=22
=23
=24
第64格
=263
=18446744073709551616
1+2+4+8+16+…+18446744073709551616=______
第1格
第2格
第3格
第4格
第5格
注:一粒米的物理重量约为0.025克 ,1亿粒大米约0.025X100000000=2500000克 2500千克 即2.5吨
通过这节课的学习,我学会了……
1. 乘方概念、及表示方法。
2.乘方的运算法则。
“乘方”精神:虽然是简简单单的重复,但结果却是惊人的。做人也要这样,脚踏实地,一步一个脚印,成功也会令你惊喜的。
今日作业:P43习题1.6 第1题
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
