3.5乘法分配律(课件)数学四年级下册(共20张PPT)青岛版
文档属性
| 名称 | 3.5乘法分配律(课件)数学四年级下册(共20张PPT)青岛版 |  | |
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 12:00:26 | ||
图片预览





文档简介
(共20张PPT)
四年级下册
3.5乘法分配律
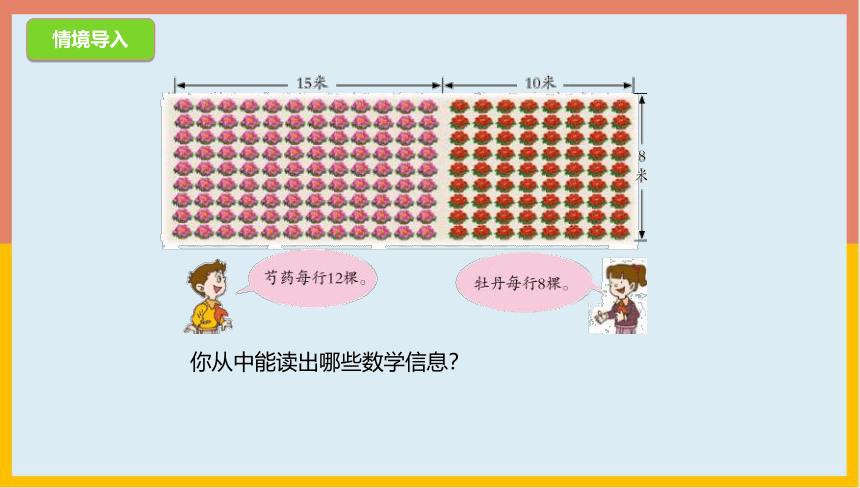
情境导入
你从中能读出哪些数学信息?
本节目标
1、使学生结合具体的实例,理解并掌握乘法交换律和结合律,初步体会应用乘法运算律进行简便计算的过程。
2、使学生经历探索积发现加法运算的过程,积累一些数学活动经验,培养观察、比较、抽象、概括积归纳等能力,发展初步的符合意识。
3、使学生在参与数学活动的过程中,获得学习成功的体验,进一步增强对数学学习的兴趣积信心。
预习反馈
1、在□里填上合适的数或字母。
(80+70)×5=80× □ +70× □
(a+b)×9=a× □ + □ × □
5 5
9 b 9
预习反馈
=357+273
=630
2、算一算,比一比
21×17+21×13 21×(17+13)
=21×30
=630
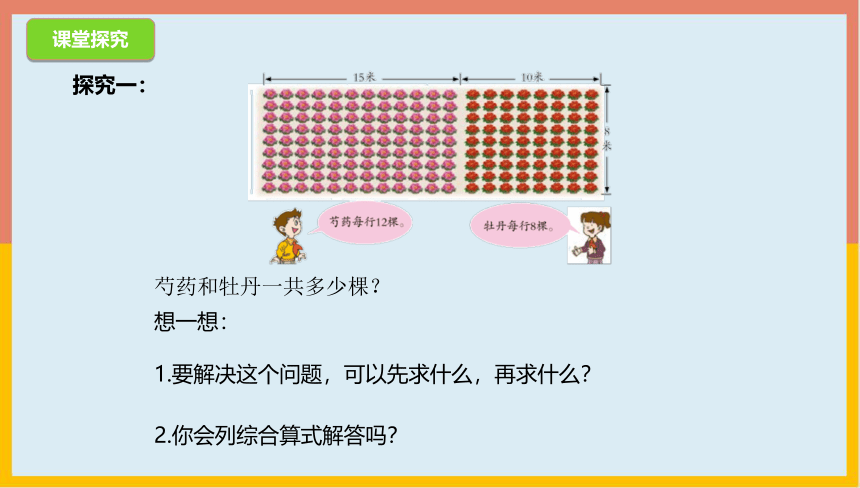
探究一:
课堂探究
想一想:
1.要解决这个问题,可以先求什么,再求什么?
2.你会列综合算式解答吗?
芍药和牡丹一共多少棵?
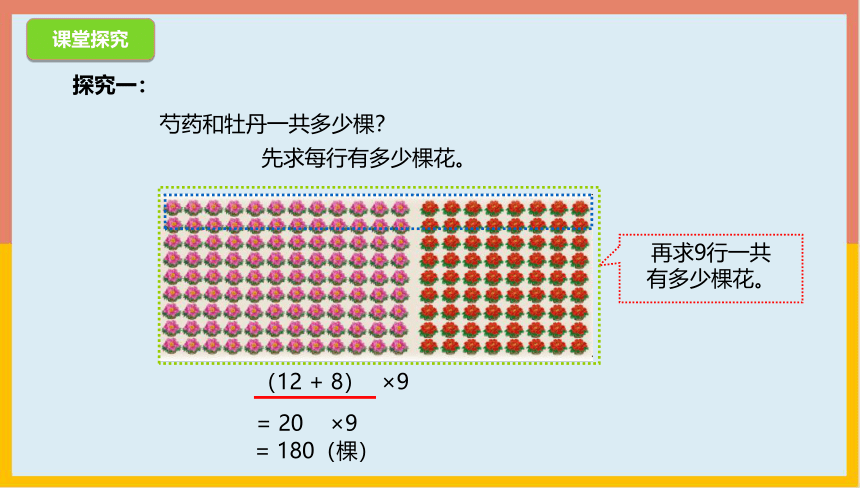
探究一:
课堂探究
(12 + 8)
芍药和牡丹一共多少棵?
= 180(棵)
= 20
先求每行有多少棵花。
再求9行一共
有多少棵花。
×9
×9
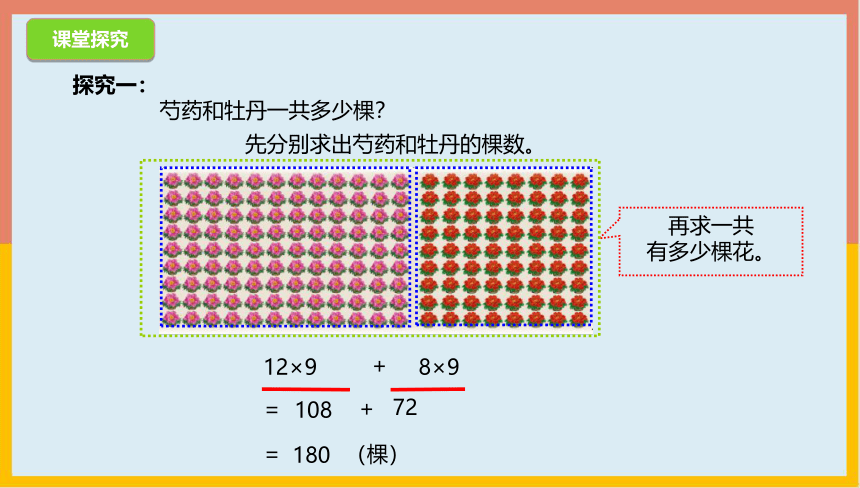
探究一:
课堂探究
芍药和牡丹一共多少棵?
先分别求出芍药和牡丹的棵数。
再求一共
有多少棵花。
8×9
12×9
=
+
72
+
(棵)
180
108
=
探究一:
课堂探究
比较两种解答方法,你发现了什么?
(12 + 8)×9
= 20×9
= 180(棵)
你能把这两道算式写成一个等式吗?
12×9+8×9
(12+8)×9
=
12×9 + 8×9
= 108 + 72
= 180(棵)
探究一:
课堂探究
芍药和牡丹的种植面积一共是多少平方米?
(15 + 10)×8
15×8 + 10×8
15×8+10×8
(15+10)×8
=
你能把这两道算式写成一个等式吗?
= 120 + 80
= 200(平方米)
= 25 ×8
= 200(平方米)
探究一:
课堂探究
两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。
通过验证,你得出了什么结论?
这个规律叫做乘法分配律。
能举例验证一下吗?你想怎样验证?
探索活动要求
3.如果数据较大,计算时可以使用计算器。
2.为确保结论的可靠性,举例验证时,较大数、较小数及特殊数(如1、0等)的例子都要有。
1.在验证卡的横线上写出两组算式。
探究二:
课堂探究
乘法分配律能用字母表示吗?
(12 + 8) ×9 = 12 × 9 + 8 × 9
+
=
你知道为什么可以这样表示吗?
(15 + 10) ×8 = 15× 8 + 10 × 8
ɑ
c
+
b
( )
·
ɑ
·
c
b
·
c
探究一:
课堂探究
(2+4)×3= 2×3 +4×3
3
5
4
(3+5)×4= 3×4 +5×4
行与列各增加1排,你还能用算式表示吗?
你能用算式表示一共有多少个圆片吗?
探究一:
课堂探究
(3+5)×4= 3×4 +5×4
4
6
5
(4+6)×5= 4×5 +6×5
ɑ·c
b·c
+
(ɑ +b )·c
=
① 236×3+ 7×236 =( + )×
② (125 + 60)× = 125×8 + 60×8
随堂检测
8
236
3
7
想一想,做一做。
随堂检测
火眼金睛辨对错。
(1)13×4+13×8=13×(4+8) ( )
(2)4×(12+13)=4×12×4×13 ( )
(3)42×99+42=42×(99+1) ( )
√
×
√
随堂检测
(1)这列火车最多能乘坐多少乘客?
(2)你还能提出什么问题?
102×12+98×12
= 200 ×12
= 2400 (人)
(102+98)×12
= 102×12+ 98×12
= 1224+ 1176
= 2400 (人)
本课小结
两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。这个规律叫做乘法分配律。
乘法分配律能用字母表示:(a+b)·c=a·c+b·c
一位数乘两位数、两位数乘两位数的计算,就是运用的乘法分配律来计算的。
乘法分配律
作业布置
1、在□里填上合适的数或字母。
236×3+236×7= □ ×( □ + □ )
m×153+m×47= □ ×( □ + □ )
2、预习第28、29、30页的有关内容。
空白演示
单击输入您的封面副标题
谢 谢 聆 听
四年级下册
3.5乘法分配律
情境导入
你从中能读出哪些数学信息?
本节目标
1、使学生结合具体的实例,理解并掌握乘法交换律和结合律,初步体会应用乘法运算律进行简便计算的过程。
2、使学生经历探索积发现加法运算的过程,积累一些数学活动经验,培养观察、比较、抽象、概括积归纳等能力,发展初步的符合意识。
3、使学生在参与数学活动的过程中,获得学习成功的体验,进一步增强对数学学习的兴趣积信心。
预习反馈
1、在□里填上合适的数或字母。
(80+70)×5=80× □ +70× □
(a+b)×9=a× □ + □ × □
5 5
9 b 9
预习反馈
=357+273
=630
2、算一算,比一比
21×17+21×13 21×(17+13)
=21×30
=630
探究一:
课堂探究
想一想:
1.要解决这个问题,可以先求什么,再求什么?
2.你会列综合算式解答吗?
芍药和牡丹一共多少棵?
探究一:
课堂探究
(12 + 8)
芍药和牡丹一共多少棵?
= 180(棵)
= 20
先求每行有多少棵花。
再求9行一共
有多少棵花。
×9
×9
探究一:
课堂探究
芍药和牡丹一共多少棵?
先分别求出芍药和牡丹的棵数。
再求一共
有多少棵花。
8×9
12×9
=
+
72
+
(棵)
180
108
=
探究一:
课堂探究
比较两种解答方法,你发现了什么?
(12 + 8)×9
= 20×9
= 180(棵)
你能把这两道算式写成一个等式吗?
12×9+8×9
(12+8)×9
=
12×9 + 8×9
= 108 + 72
= 180(棵)
探究一:
课堂探究
芍药和牡丹的种植面积一共是多少平方米?
(15 + 10)×8
15×8 + 10×8
15×8+10×8
(15+10)×8
=
你能把这两道算式写成一个等式吗?
= 120 + 80
= 200(平方米)
= 25 ×8
= 200(平方米)
探究一:
课堂探究
两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。
通过验证,你得出了什么结论?
这个规律叫做乘法分配律。
能举例验证一下吗?你想怎样验证?
探索活动要求
3.如果数据较大,计算时可以使用计算器。
2.为确保结论的可靠性,举例验证时,较大数、较小数及特殊数(如1、0等)的例子都要有。
1.在验证卡的横线上写出两组算式。
探究二:
课堂探究
乘法分配律能用字母表示吗?
(12 + 8) ×9 = 12 × 9 + 8 × 9
+
=
你知道为什么可以这样表示吗?
(15 + 10) ×8 = 15× 8 + 10 × 8
ɑ
c
+
b
( )
·
ɑ
·
c
b
·
c
探究一:
课堂探究
(2+4)×3= 2×3 +4×3
3
5
4
(3+5)×4= 3×4 +5×4
行与列各增加1排,你还能用算式表示吗?
你能用算式表示一共有多少个圆片吗?
探究一:
课堂探究
(3+5)×4= 3×4 +5×4
4
6
5
(4+6)×5= 4×5 +6×5
ɑ·c
b·c
+
(ɑ +b )·c
=
① 236×3+ 7×236 =( + )×
② (125 + 60)× = 125×8 + 60×8
随堂检测
8
236
3
7
想一想,做一做。
随堂检测
火眼金睛辨对错。
(1)13×4+13×8=13×(4+8) ( )
(2)4×(12+13)=4×12×4×13 ( )
(3)42×99+42=42×(99+1) ( )
√
×
√
随堂检测
(1)这列火车最多能乘坐多少乘客?
(2)你还能提出什么问题?
102×12+98×12
= 200 ×12
= 2400 (人)
(102+98)×12
= 102×12+ 98×12
= 1224+ 1176
= 2400 (人)
本课小结
两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。这个规律叫做乘法分配律。
乘法分配律能用字母表示:(a+b)·c=a·c+b·c
一位数乘两位数、两位数乘两位数的计算,就是运用的乘法分配律来计算的。
乘法分配律
作业布置
1、在□里填上合适的数或字母。
236×3+236×7= □ ×( □ + □ )
m×153+m×47= □ ×( □ + □ )
2、预习第28、29、30页的有关内容。
空白演示
单击输入您的封面副标题
谢 谢 聆 听
