2022中考专题九年级下册第三章 圆 视图与投影 复习课件(共17张PPT)
文档属性
| 名称 | 2022中考专题九年级下册第三章 圆 视图与投影 复习课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-25 08:54:43 | ||
图片预览


文档简介
(共17张PPT)
视图与投影
中考一轮复习
视图与投影
投 影
视 图
中心投影
平行投影
圆柱、球、圆锥、棱柱等三视图
正方体
计 算
展开图
组合体三视图
中考考点梳理
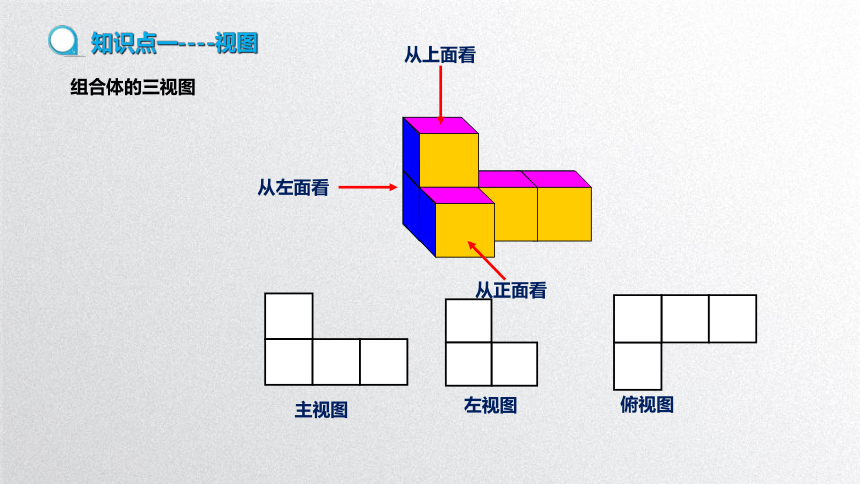
从上面看
从左面看
从正面看
主视图
左视图
俯视图
组合体的三视图
知识点一----视图
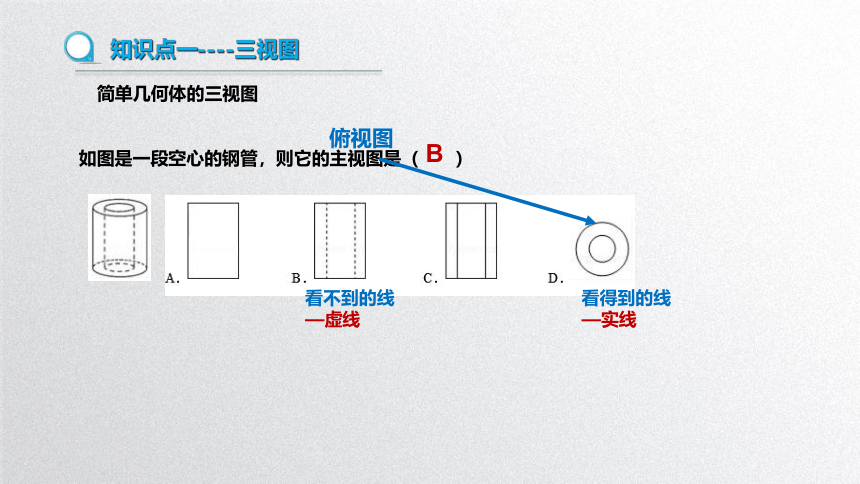
知识点一----三视图
如图是一段空心的钢管,则它的主视图是( )
看不到的线
—虚线
看得到的线
—实线
俯视图
简单几何体的三视图
B
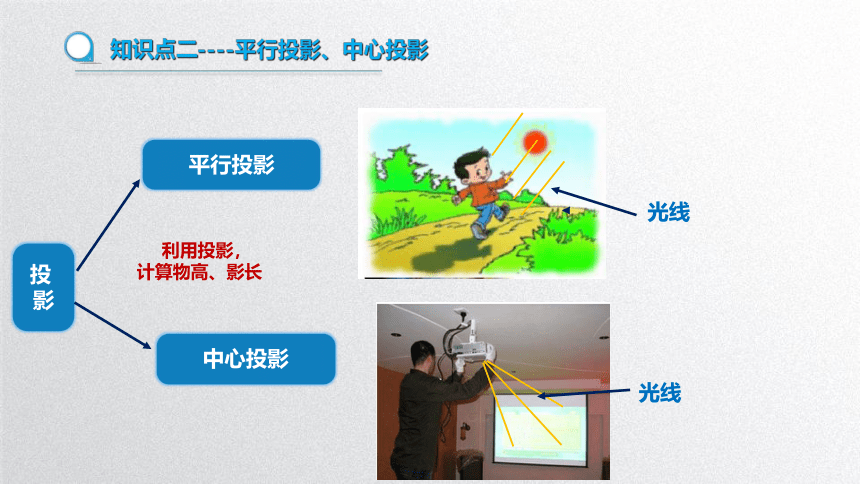
知识点二----平行投影、中心投影
平行投影
中心投影
光线
光线
利用投影,
计算物高、影长
投
影
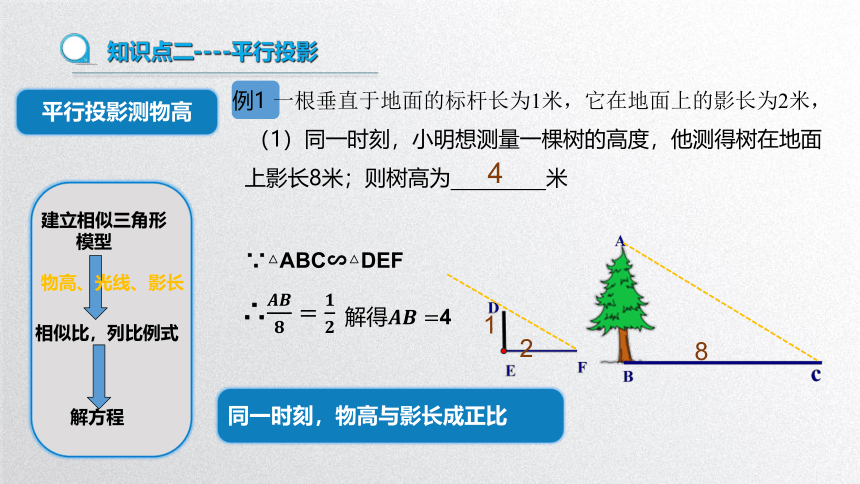
知识点二----平行投影
例1 一根垂直于地面的标杆长为1米,它在地面上的影长为2米,
(1)同一时刻,小明想测量一棵树的高度,他测得树在地面上影长8米;则树高为 米
平行投影测物高
建立相似三角形
模型
相似比,列比例式
解方程
∴
∵△ABC∽△DEF
4
物高、光线、影长
8
1
2
4
同一时刻,物高与影长成正比
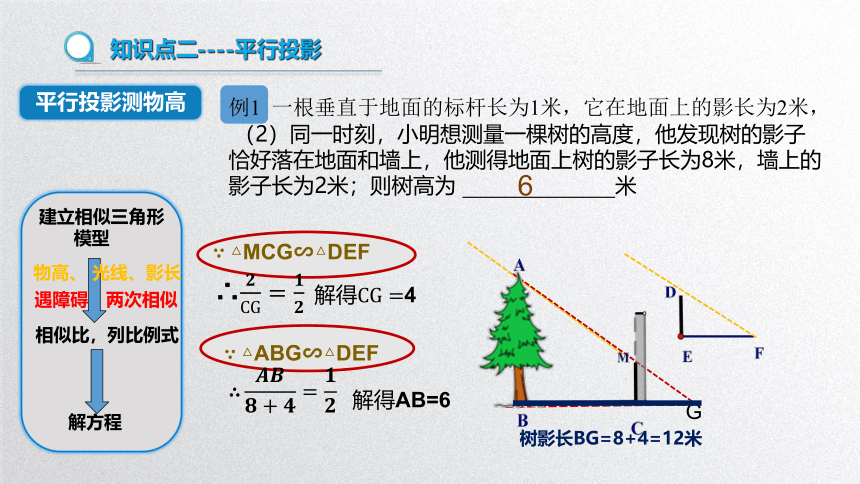
知识点二----平行投影
例1 一根垂直于地面的标杆长为1米,它在地面上的影长为2米,
(2)同一时刻,小明想测量一棵树的高度,他发现树的影子恰好落在地面和墙上,他测得地面上树的影子长为8米,墙上的影子长为2米;则树高为 米
平行投影测物高
G
∴
∵ △ABG∽△DEF
AB=6
∵ △MCG∽△DEF
4
建立相似三角形
模型
相似比,列比例式
解方程
遇障碍,两次相似
6
物高、 光线、影长
树影长BG=8+4=12米
知识点二----平行投影
例1 一根垂直于地面的标杆长为1米,它在地面上的影长为2米,
(2)同一时刻,小明想测量一棵树的高度,他发现树的影子恰好落在地面和墙上,他测得地面上树的影子长为8米,墙上的影子长为2米;则树高为 米
平行投影测物高
G
∵ △AMG∽△DEF
AG=4
建立相似三角形
模型
相似比,列比例式
解方程
遇障碍,分割图形
6
解法2:
过M作MG⊥AB于G,则四边形BCMG是矩形
∴MG=BC=8;BG=MC=2
AB=4+2=6米
解法多样,
本质相同
知识点二----平行投影
例1 一根垂直于地面的标杆长为1米,它在地面上的影长为2米,
(3)同一时刻,小明想测量一棵树的高度,已知树的影子落在地上和斜坡上,如图所示。测得地面上的影长为8米,坡面上的影长为2米.已知斜坡的坡角为30°,则树高为 米
∵△ABG∽△DEF
AB=5+
∵△MHG∽△DEF
2
Rt△MCH中 ∠MCH=30°,M=2
∴MH=1,CH=
建立相似三角形
模型
相似比,列比例式
解方程
平行投影测物高
G
5+
H
树影长BG= 2=(10+ )米
解直角三角形
遇障碍,两次相似
物高、光线、影长
知识点二----平行投影
例1 一根长为1米,垂直于地面的标杆在地面上的影长为2米,
(3)同一时刻,小明想测量一棵树的高度,他发现树的影子落在地上和斜坡上,如图所示。测得地面上的影长为8米,坡面上的影长为2米.已知斜坡的坡角为30°,则树高为 米
∵△AMG∽△DEF
在Rt△MCH中 ∠MCH=30°,M=2
∴MH=1,CH=
建立相似三角形
模型
相似比列比例式
解方程
物高、光线、影长
遇障碍,分割图形
平行投影测物高
5+
H
G
解法2:过点M作MH垂直BC于H,MG垂直AB于G,则四边形BHMG是矩形
∴AB=AG+BG=5+
∴BG=MH=1,MG=
解法多样,
本质相同
平行投影测物高
平行
投影
物高
物高
光线
影长
标杆高、
光线
影长
测
知识点二----中心投影
例2 身高1.6米的小明站在D处,测得他在路灯A下的影长DE=1.5米,小明与路灯距离BD=4.5米,
(1)路灯与地面的距离AB为 米
中心投影测物高
∵△ABE∽△CDE
AB=6.4
相似三角形模型
相似比,列比例式
解方程
6.4
物高、光线、影长
知识点二----中心投影
(2)如图,小明前方5.5米处有棵小树,若测得小树影长FH=4米,且F、H在BE直线上,则树高为 米
∵△ABH∽△GFH
GF=
∴
例2 身高1.6米的小明站在D处,测得他在路灯A下的影长DE=1.5米,小明与路灯距离BD=4.5米,
(1)路灯与地面的距离AB为 米
H
G
建立相似三角形
模型
相似比,列比例式
解方程
中心投影测物高
6.4
物高、光线、影长
知识点二----中心投影
小明前方5.5米处有棵小树,若测得小树影长FH=4米,且F、H在BE直线上,则树高为 米
例2 身高1.6米的小明站在D处,测得他在路灯A下的影长DE=1.5米,小明与路灯距离BD=4.5米,
H
G
中心投影测物高
两次投影,两次相似
中心投影测物高
中心
投影
物高
光线
影长
灯 高
物 高
测
回顾反思,形成知识链
实际问题,建立几何模型,列方程求解
方法一致性
视图与投影
中考一轮复习
视图与投影
投 影
视 图
中心投影
平行投影
圆柱、球、圆锥、棱柱等三视图
正方体
计 算
展开图
组合体三视图
中考考点梳理
从上面看
从左面看
从正面看
主视图
左视图
俯视图
组合体的三视图
知识点一----视图
知识点一----三视图
如图是一段空心的钢管,则它的主视图是( )
看不到的线
—虚线
看得到的线
—实线
俯视图
简单几何体的三视图
B
知识点二----平行投影、中心投影
平行投影
中心投影
光线
光线
利用投影,
计算物高、影长
投
影
知识点二----平行投影
例1 一根垂直于地面的标杆长为1米,它在地面上的影长为2米,
(1)同一时刻,小明想测量一棵树的高度,他测得树在地面上影长8米;则树高为 米
平行投影测物高
建立相似三角形
模型
相似比,列比例式
解方程
∴
∵△ABC∽△DEF
4
物高、光线、影长
8
1
2
4
同一时刻,物高与影长成正比
知识点二----平行投影
例1 一根垂直于地面的标杆长为1米,它在地面上的影长为2米,
(2)同一时刻,小明想测量一棵树的高度,他发现树的影子恰好落在地面和墙上,他测得地面上树的影子长为8米,墙上的影子长为2米;则树高为 米
平行投影测物高
G
∴
∵ △ABG∽△DEF
AB=6
∵ △MCG∽△DEF
4
建立相似三角形
模型
相似比,列比例式
解方程
遇障碍,两次相似
6
物高、 光线、影长
树影长BG=8+4=12米
知识点二----平行投影
例1 一根垂直于地面的标杆长为1米,它在地面上的影长为2米,
(2)同一时刻,小明想测量一棵树的高度,他发现树的影子恰好落在地面和墙上,他测得地面上树的影子长为8米,墙上的影子长为2米;则树高为 米
平行投影测物高
G
∵ △AMG∽△DEF
AG=4
建立相似三角形
模型
相似比,列比例式
解方程
遇障碍,分割图形
6
解法2:
过M作MG⊥AB于G,则四边形BCMG是矩形
∴MG=BC=8;BG=MC=2
AB=4+2=6米
解法多样,
本质相同
知识点二----平行投影
例1 一根垂直于地面的标杆长为1米,它在地面上的影长为2米,
(3)同一时刻,小明想测量一棵树的高度,已知树的影子落在地上和斜坡上,如图所示。测得地面上的影长为8米,坡面上的影长为2米.已知斜坡的坡角为30°,则树高为 米
∵△ABG∽△DEF
AB=5+
∵△MHG∽△DEF
2
Rt△MCH中 ∠MCH=30°,M=2
∴MH=1,CH=
建立相似三角形
模型
相似比,列比例式
解方程
平行投影测物高
G
5+
H
树影长BG= 2=(10+ )米
解直角三角形
遇障碍,两次相似
物高、光线、影长
知识点二----平行投影
例1 一根长为1米,垂直于地面的标杆在地面上的影长为2米,
(3)同一时刻,小明想测量一棵树的高度,他发现树的影子落在地上和斜坡上,如图所示。测得地面上的影长为8米,坡面上的影长为2米.已知斜坡的坡角为30°,则树高为 米
∵△AMG∽△DEF
在Rt△MCH中 ∠MCH=30°,M=2
∴MH=1,CH=
建立相似三角形
模型
相似比列比例式
解方程
物高、光线、影长
遇障碍,分割图形
平行投影测物高
5+
H
G
解法2:过点M作MH垂直BC于H,MG垂直AB于G,则四边形BHMG是矩形
∴AB=AG+BG=5+
∴BG=MH=1,MG=
解法多样,
本质相同
平行投影测物高
平行
投影
物高
物高
光线
影长
标杆高、
光线
影长
测
知识点二----中心投影
例2 身高1.6米的小明站在D处,测得他在路灯A下的影长DE=1.5米,小明与路灯距离BD=4.5米,
(1)路灯与地面的距离AB为 米
中心投影测物高
∵△ABE∽△CDE
AB=6.4
相似三角形模型
相似比,列比例式
解方程
6.4
物高、光线、影长
知识点二----中心投影
(2)如图,小明前方5.5米处有棵小树,若测得小树影长FH=4米,且F、H在BE直线上,则树高为 米
∵△ABH∽△GFH
GF=
∴
例2 身高1.6米的小明站在D处,测得他在路灯A下的影长DE=1.5米,小明与路灯距离BD=4.5米,
(1)路灯与地面的距离AB为 米
H
G
建立相似三角形
模型
相似比,列比例式
解方程
中心投影测物高
6.4
物高、光线、影长
知识点二----中心投影
小明前方5.5米处有棵小树,若测得小树影长FH=4米,且F、H在BE直线上,则树高为 米
例2 身高1.6米的小明站在D处,测得他在路灯A下的影长DE=1.5米,小明与路灯距离BD=4.5米,
H
G
中心投影测物高
两次投影,两次相似
中心投影测物高
中心
投影
物高
光线
影长
灯 高
物 高
测
回顾反思,形成知识链
实际问题,建立几何模型,列方程求解
方法一致性
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
