华东师大版数学八年级上册 13.3.1 等腰三角形的性质课件(共23张PPT)
文档属性
| 名称 | 华东师大版数学八年级上册 13.3.1 等腰三角形的性质课件(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 21:09:49 | ||
图片预览




文档简介
(共23张PPT)
创 设 情 景
如图所示,建筑工人在盖房子时,用一块等腰三角板放在房梁上,从顶点系一重物,如果系重物的绳子正好经过三角板底边中点,就说房梁是水平的,你知道其中反映了什么数学原理
创 设 情 景
提取关键词:等腰三角板,
底边中点,水平
等腰三角形
13.3.1 等腰三角形的性质
华师版数学教材
对于等腰三角形,
我们已经了解了哪些方面的知识?
温 故 而 知 新(1)
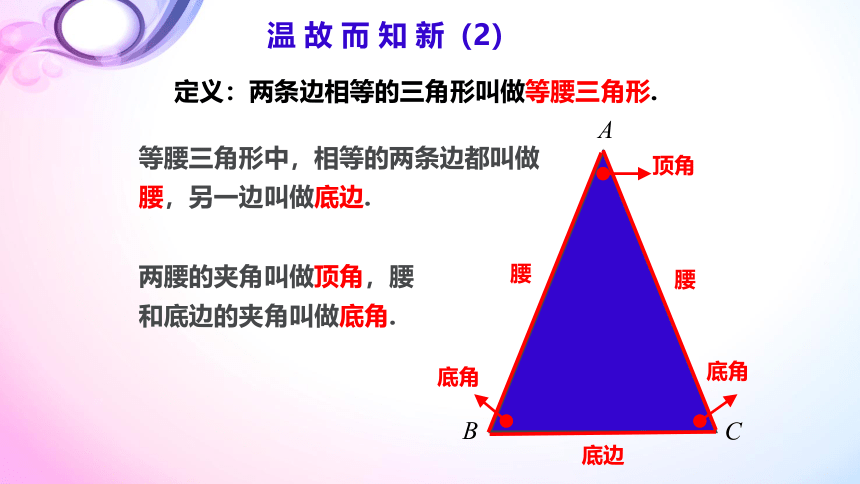
定义:两条边相等的三角形叫做等腰三角形.
等腰三角形中,相等的两条边都叫做腰,另一边叫做底边.
温 故 而 知 新(2)
两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
顶角
腰
腰
底角
底角
底边
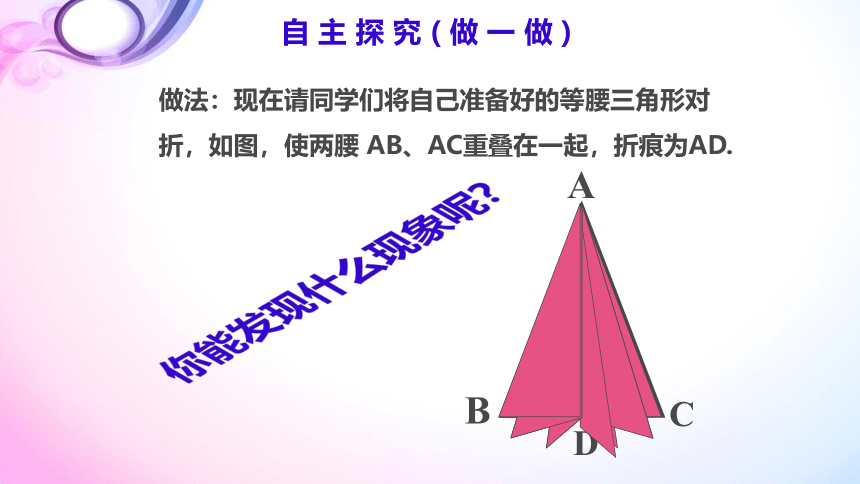
做法:现在请同学们将自己准备好的等腰三角形对折,如图,使两腰 AB、AC重叠在一起,折痕为AD.
D
A
B
C
自 主 探 究 ( 做 一 做 )
等腰三角形是轴对称图形,顶角平分线所在的直线是它的对称轴.
A
B
C
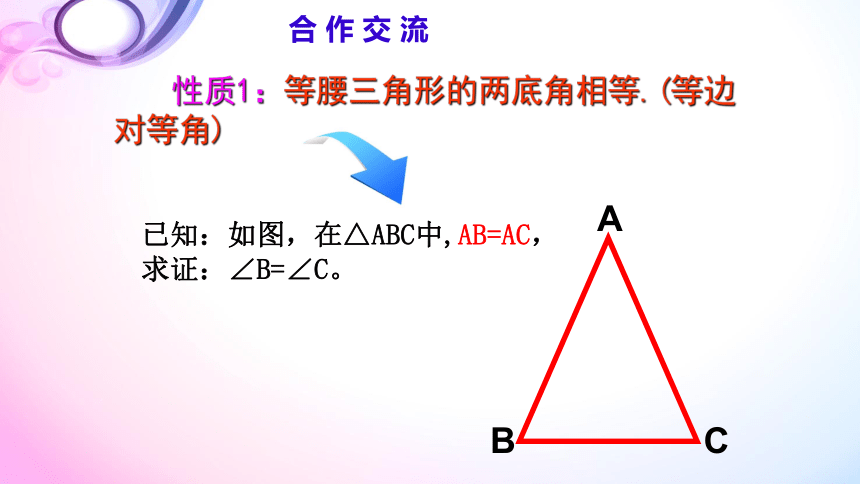
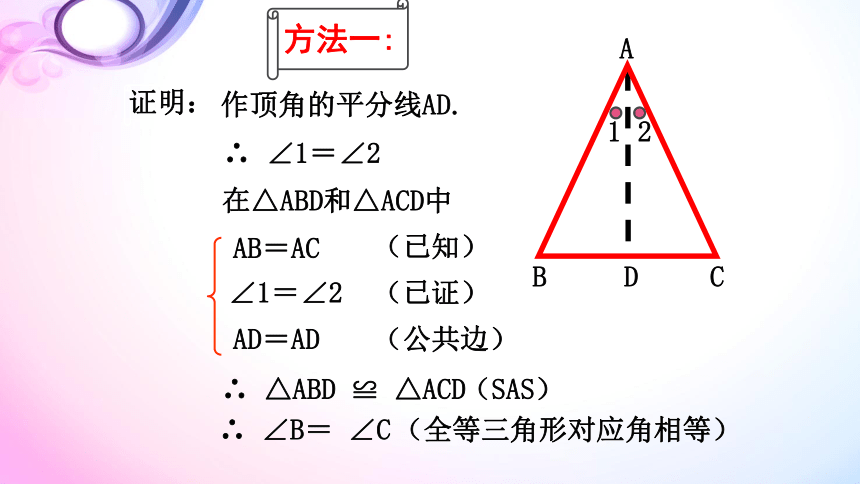
已知:如图,在△ABC中,AB=AC,
求证:∠B=∠C。
性质1:等腰三角形的两底角相等.(等边对等角)
合 作 交 流
A
B
C
证明:
∴ ∠1=∠2
D
1
2
在△ABD和△ACD中
作顶角的平分线AD.
AB=AC
(已知)
∠1=∠2
(已证)
AD=AD
(公共边)
∴ △ABD ≌ △ACD
(SAS)
∴ ∠B= ∠C
(全等三角形对应角相等)
方法一:
作△ABC的BC边上的中线AD.
方法二:
D
A
B
C
例1 已知:在△ABC中,AB=AC,∠B=80o.
求∠C和∠A的大小.
解:∵AB=AC (已知)
∴∠C=∠B=80o (等边对等角),
又∵∠A+∠B+∠C=180o (三角形的内角和等于180o),
∴∠A=180o-∠B-∠C (等式的性质)
=180o-80o-80o=20o
练习1:已知:在△ABC中,AB=AC,∠A=80o,求
∠C和∠B的度数.
∵ AB=AC,
∴ ∠C=∠B( 等边对等角)
∵ ∠A+∠B +∠C=180。(三角形内角
和等于180。)
∠A=80 。
∴ ∠B=∠C=50。
看 我 72 变
解:
要记住哦!!
在等腰三角形中,已知一个角,可以求出另外两个角.
自 主 探 究
想一想:由前面的“做一做”,除了
能得到∠B=∠C外,你还可以发现什
么结论?
A
B
C
D
1
2
作顶角的平分线AD,则AD是
△ABC的角平分线.
证明了△ABD≌ △ACD
除了得到∠B=∠C外,
还可以得到:
BD=CD
即AD是BC边上的中线;
即AD是BC边上的高 .
∠ADB =∠ADC=90°
合 作 交 流
刚才证明:等腰三角形的顶角平分线平分底边并且垂直于底边。
也就是说:
性质2:等腰三角形底边上的高、中线及顶角的平分线互相重合.(三线合一)
合 作 交 流
“三 线 合 一”的 操 作
一、填空(用符号语言表示等腰三角形的性质2)
如图,在△ABC中,AB=AC时,
1、∵∠BAD =∠CAD,∴ ____=___,___⊥___.
2、∵BD=CD,∴ ∠___ = ∠____,___ ⊥___.
3、∵AD⊥BC,∴ ∠____= ∠____,___=___.
C
A
B
D
BAD
CAD
BD
CD
BAD
CAD
AD
BC
BD
CD
AD
BC
展 示 提 升
例2 如图,在△ABC中,AB=AC,D是BC边上的中点,∠B = 36°.求: (1)∠ADC的大小;(2)∠1的大小.
解:(1)∵AB=AC, BD=DC(已知)
A
D
B
C
1
展 示 提 升
∴AD⊥BC(等腰三角形的“三线合一”),
∴∠ADC= ∠ADB=90°.
(2) ∵ ∠1+∠B+∠ADB= 180°(三角形的内角和等于180°),
∠B=36°(已知),
∴∠1=180°-∠B-∠ADB(等式的性质)
=180°-36°-90°=54°.
练习2:如图,AB=AC,∠B= 36°,点D在BC上,且∠DAC=54°.求证:BD=CD.
A
D
C
B
看 我 72 变
建筑工人在盖房子时,用一块等腰三角板放在房梁上,
从顶点系一重物,如果系重物的绳子正好经过三角板底
边中点,就说房梁是水平的,你知道其中反映了
什么数学原理
解 答 情 景
视频对话
问题描述
等腰三角形“三线合一”
2.等腰三角形的两底角相等. (简写成“等边对等角”);
3.等腰三角形底边上的高、中线及顶角的平分线
互相重合.(简称“三线合一”)
1.等腰三角形是轴对称图形;
要记得哦!!
必做题:课本P81,练习1、2、3题;
选做题:课本P81,练习4题.
分 层 作 业
后续:等腰三角形的判定
谢 谢 !
创 设 情 景
如图所示,建筑工人在盖房子时,用一块等腰三角板放在房梁上,从顶点系一重物,如果系重物的绳子正好经过三角板底边中点,就说房梁是水平的,你知道其中反映了什么数学原理
创 设 情 景
提取关键词:等腰三角板,
底边中点,水平
等腰三角形
13.3.1 等腰三角形的性质
华师版数学教材
对于等腰三角形,
我们已经了解了哪些方面的知识?
温 故 而 知 新(1)
定义:两条边相等的三角形叫做等腰三角形.
等腰三角形中,相等的两条边都叫做腰,另一边叫做底边.
温 故 而 知 新(2)
两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
顶角
腰
腰
底角
底角
底边
做法:现在请同学们将自己准备好的等腰三角形对折,如图,使两腰 AB、AC重叠在一起,折痕为AD.
D
A
B
C
自 主 探 究 ( 做 一 做 )
等腰三角形是轴对称图形,顶角平分线所在的直线是它的对称轴.
A
B
C
已知:如图,在△ABC中,AB=AC,
求证:∠B=∠C。
性质1:等腰三角形的两底角相等.(等边对等角)
合 作 交 流
A
B
C
证明:
∴ ∠1=∠2
D
1
2
在△ABD和△ACD中
作顶角的平分线AD.
AB=AC
(已知)
∠1=∠2
(已证)
AD=AD
(公共边)
∴ △ABD ≌ △ACD
(SAS)
∴ ∠B= ∠C
(全等三角形对应角相等)
方法一:
作△ABC的BC边上的中线AD.
方法二:
D
A
B
C
例1 已知:在△ABC中,AB=AC,∠B=80o.
求∠C和∠A的大小.
解:∵AB=AC (已知)
∴∠C=∠B=80o (等边对等角),
又∵∠A+∠B+∠C=180o (三角形的内角和等于180o),
∴∠A=180o-∠B-∠C (等式的性质)
=180o-80o-80o=20o
练习1:已知:在△ABC中,AB=AC,∠A=80o,求
∠C和∠B的度数.
∵ AB=AC,
∴ ∠C=∠B( 等边对等角)
∵ ∠A+∠B +∠C=180。(三角形内角
和等于180。)
∠A=80 。
∴ ∠B=∠C=50。
看 我 72 变
解:
要记住哦!!
在等腰三角形中,已知一个角,可以求出另外两个角.
自 主 探 究
想一想:由前面的“做一做”,除了
能得到∠B=∠C外,你还可以发现什
么结论?
A
B
C
D
1
2
作顶角的平分线AD,则AD是
△ABC的角平分线.
证明了△ABD≌ △ACD
除了得到∠B=∠C外,
还可以得到:
BD=CD
即AD是BC边上的中线;
即AD是BC边上的高 .
∠ADB =∠ADC=90°
合 作 交 流
刚才证明:等腰三角形的顶角平分线平分底边并且垂直于底边。
也就是说:
性质2:等腰三角形底边上的高、中线及顶角的平分线互相重合.(三线合一)
合 作 交 流
“三 线 合 一”的 操 作
一、填空(用符号语言表示等腰三角形的性质2)
如图,在△ABC中,AB=AC时,
1、∵∠BAD =∠CAD,∴ ____=___,___⊥___.
2、∵BD=CD,∴ ∠___ = ∠____,___ ⊥___.
3、∵AD⊥BC,∴ ∠____= ∠____,___=___.
C
A
B
D
BAD
CAD
BD
CD
BAD
CAD
AD
BC
BD
CD
AD
BC
展 示 提 升
例2 如图,在△ABC中,AB=AC,D是BC边上的中点,∠B = 36°.求: (1)∠ADC的大小;(2)∠1的大小.
解:(1)∵AB=AC, BD=DC(已知)
A
D
B
C
1
展 示 提 升
∴AD⊥BC(等腰三角形的“三线合一”),
∴∠ADC= ∠ADB=90°.
(2) ∵ ∠1+∠B+∠ADB= 180°(三角形的内角和等于180°),
∠B=36°(已知),
∴∠1=180°-∠B-∠ADB(等式的性质)
=180°-36°-90°=54°.
练习2:如图,AB=AC,∠B= 36°,点D在BC上,且∠DAC=54°.求证:BD=CD.
A
D
C
B
看 我 72 变
建筑工人在盖房子时,用一块等腰三角板放在房梁上,
从顶点系一重物,如果系重物的绳子正好经过三角板底
边中点,就说房梁是水平的,你知道其中反映了
什么数学原理
解 答 情 景
视频对话
问题描述
等腰三角形“三线合一”
2.等腰三角形的两底角相等. (简写成“等边对等角”);
3.等腰三角形底边上的高、中线及顶角的平分线
互相重合.(简称“三线合一”)
1.等腰三角形是轴对称图形;
要记得哦!!
必做题:课本P81,练习1、2、3题;
选做题:课本P81,练习4题.
分 层 作 业
后续:等腰三角形的判定
谢 谢 !
