华东师大版数学八年级上册 14.1.1 直角三角形三边的关系(1) 课件(共15张)
文档属性
| 名称 | 华东师大版数学八年级上册 14.1.1 直角三角形三边的关系(1) 课件(共15张) |  | |
| 格式 | pptx | ||
| 文件大小 | 747.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-25 09:56:12 | ||
图片预览



文档简介
(共15张PPT)
直角三角形三边的关系
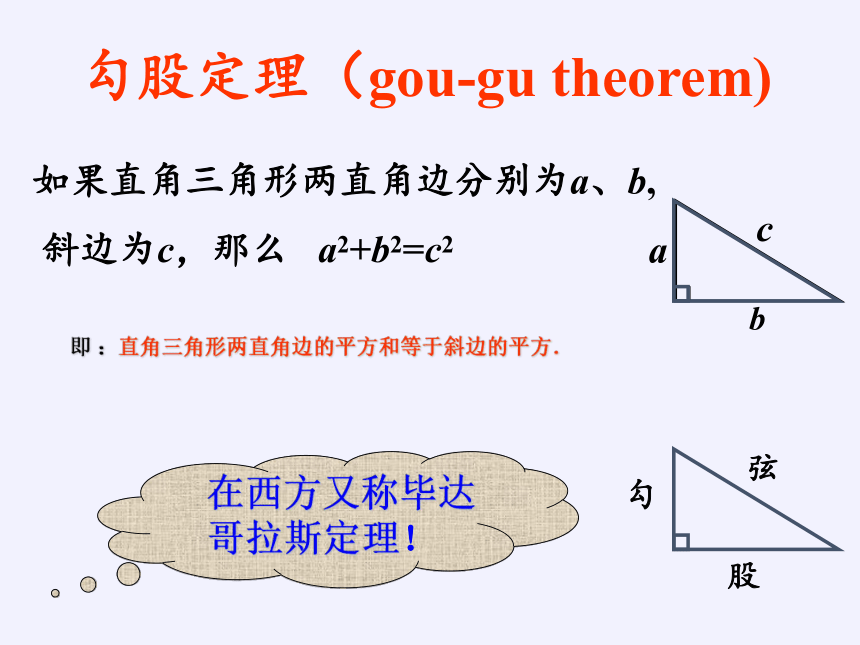
勾股定理(gou-gu theorem)
如果直角三角形两直角边分别为a、b,
斜边为c,那么 a2+b2=c2
即 :直角三角形两直角边的平方和等于斜边的平方.
a
b
c
勾
股
弦
在西方又称毕达哥拉斯定理!
在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
两千多年前,古希腊有个哥拉
斯学派,他们首先发现了勾股定理,因此
在国外人们通常称勾股定理为毕达哥拉斯
年希腊曾经发行了一枚纪念票。
定理。为了纪念毕达哥拉斯学派,1955
勾 股 世 界
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前
两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。
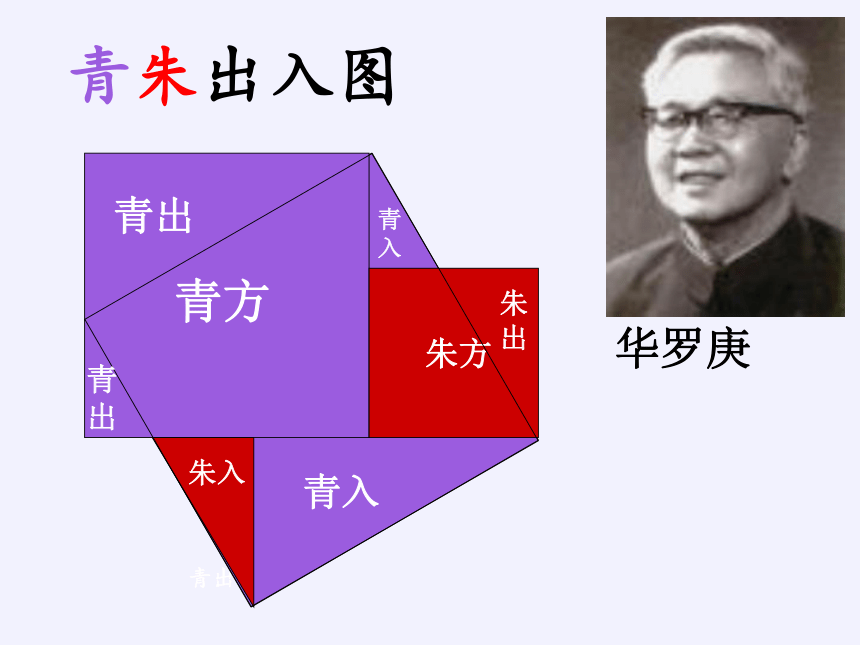
青出
朱入
朱出
朱方
青方
青入
青入
青出
青出
华罗庚
青朱出入图
朱入
朱出
c
a
b
c
a
b
c
a
b
c
a
b
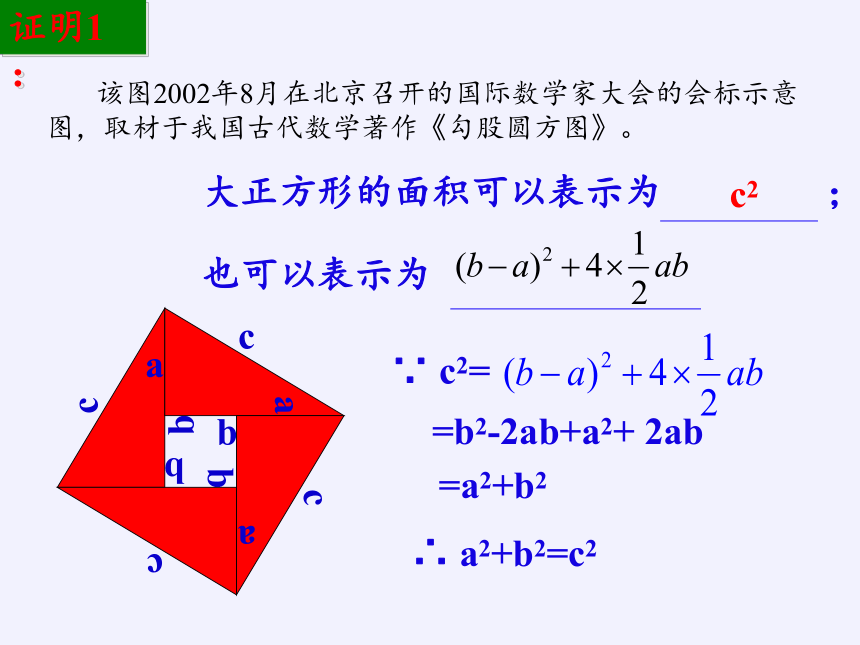
∵ c2=
=b2-2ab+a2+ 2ab
=a2+b2
∴ a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
c2
该图2002年8月在北京召开的国际数学家大会的会标示意图,取材于我国古代数学著作《勾股圆方图》。
证明1:
c
a
b
c
a
b
c
a
b
c
a
b
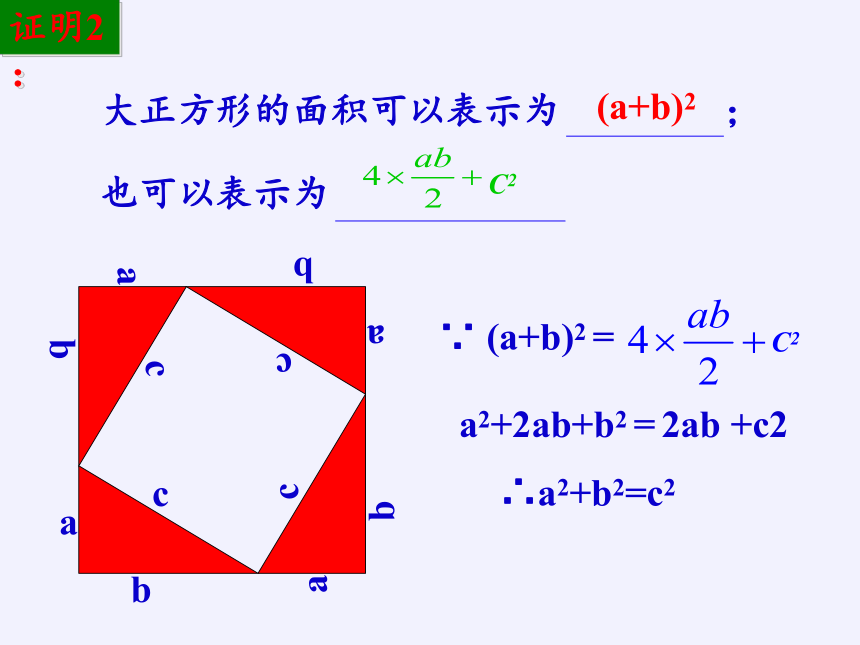
∵ (a+b)2 =
a2+2ab+b2 = 2ab +c2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
(a+b)2
C2
证明2:
C2
1876年4月1日,伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证法。
1881年,伽菲尔德就任美国第20任总统。后来,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统证法”。
勾股定理的证明方法
证法一
证法二
证法三
(邹元治证明)
(赵爽证明) 赵爽:我国古代数学家
走进数学史
勾股定理的证明方法
证法四
证法五
证法六
(加菲尔德证明) 加菲尔德:第二十任总统
(梅文鼎证明) 梅文鼎:清代天文、数学家
(项明达证明) 项明达:清代数学家
走进数学史
比一比看看谁算得快!
2.求下列直角三角形中未知边的长:
可用勾股定理建立方程.
方法小结:
8
x
17
16
20
x
12
5
x
做一做
1
1
美丽的勾股树
1.在等腰△ABC中,AB=AC=13cm,BC=10cm,求△ABC的面积
2.欲做一块矩形展板,将由一小型货车运载(附此货车数据:车厢长3cm,宽1.5m,高2cm,)为防止运送途中展板的损坏,要求展板的一边紧贴车厢侧门底边,问:这块展板的长宽如何设计,才能使它的面积最大?
小结
今天我们
学习了
一个定理——勾股定理
一个思想——以形证数的思想
一次探索——由特殊到一般的探索过程
增添了
一份自豪——中国的自豪
谢 谢
直角三角形三边的关系
勾股定理(gou-gu theorem)
如果直角三角形两直角边分别为a、b,
斜边为c,那么 a2+b2=c2
即 :直角三角形两直角边的平方和等于斜边的平方.
a
b
c
勾
股
弦
在西方又称毕达哥拉斯定理!
在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
两千多年前,古希腊有个哥拉
斯学派,他们首先发现了勾股定理,因此
在国外人们通常称勾股定理为毕达哥拉斯
年希腊曾经发行了一枚纪念票。
定理。为了纪念毕达哥拉斯学派,1955
勾 股 世 界
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前
两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。
青出
朱入
朱出
朱方
青方
青入
青入
青出
青出
华罗庚
青朱出入图
朱入
朱出
c
a
b
c
a
b
c
a
b
c
a
b
∵ c2=
=b2-2ab+a2+ 2ab
=a2+b2
∴ a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
c2
该图2002年8月在北京召开的国际数学家大会的会标示意图,取材于我国古代数学著作《勾股圆方图》。
证明1:
c
a
b
c
a
b
c
a
b
c
a
b
∵ (a+b)2 =
a2+2ab+b2 = 2ab +c2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
(a+b)2
C2
证明2:
C2
1876年4月1日,伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证法。
1881年,伽菲尔德就任美国第20任总统。后来,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统证法”。
勾股定理的证明方法
证法一
证法二
证法三
(邹元治证明)
(赵爽证明) 赵爽:我国古代数学家
走进数学史
勾股定理的证明方法
证法四
证法五
证法六
(加菲尔德证明) 加菲尔德:第二十任总统
(梅文鼎证明) 梅文鼎:清代天文、数学家
(项明达证明) 项明达:清代数学家
走进数学史
比一比看看谁算得快!
2.求下列直角三角形中未知边的长:
可用勾股定理建立方程.
方法小结:
8
x
17
16
20
x
12
5
x
做一做
1
1
美丽的勾股树
1.在等腰△ABC中,AB=AC=13cm,BC=10cm,求△ABC的面积
2.欲做一块矩形展板,将由一小型货车运载(附此货车数据:车厢长3cm,宽1.5m,高2cm,)为防止运送途中展板的损坏,要求展板的一边紧贴车厢侧门底边,问:这块展板的长宽如何设计,才能使它的面积最大?
小结
今天我们
学习了
一个定理——勾股定理
一个思想——以形证数的思想
一次探索——由特殊到一般的探索过程
增添了
一份自豪——中国的自豪
谢 谢
