2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册3.3.1抛物线及其标准方程课件(36张ppt)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册3.3.1抛物线及其标准方程课件(36张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-25 14:06:39 | ||
图片预览










文档简介
(共36张PPT)
F佳
抛物线及其标准方程
赵州桥
喷泉
探照灯
生活中存在着各种形式的抛物线
500米口径球面射电望远镜:天眼
球在空中运动的轨迹是抛物线。
抛物线到底有怎样的几何特征?
抛物线方程又有什么样的形式呢?
y
x
o
二次函数是开口向上或向下的抛物线。
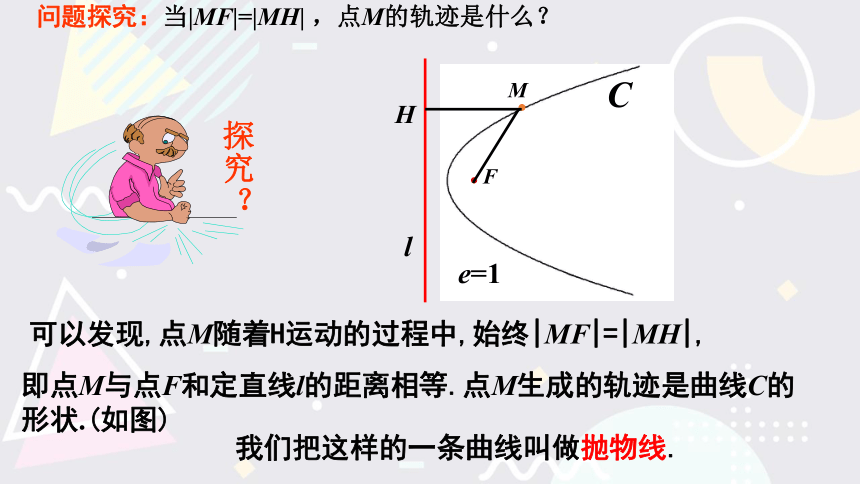
问题探究:当|MF|=|MH| ,点M的轨迹是什么?
探究?
可以发现,点M随着H运动的过程中,始终|MF|=|MH|,
即点M与点F和定直线l的距离相等.点M生成的轨迹是曲线C的形状.(如图)
M
·
F
l
·
e=1
我们把这样的一条曲线叫做抛物线.
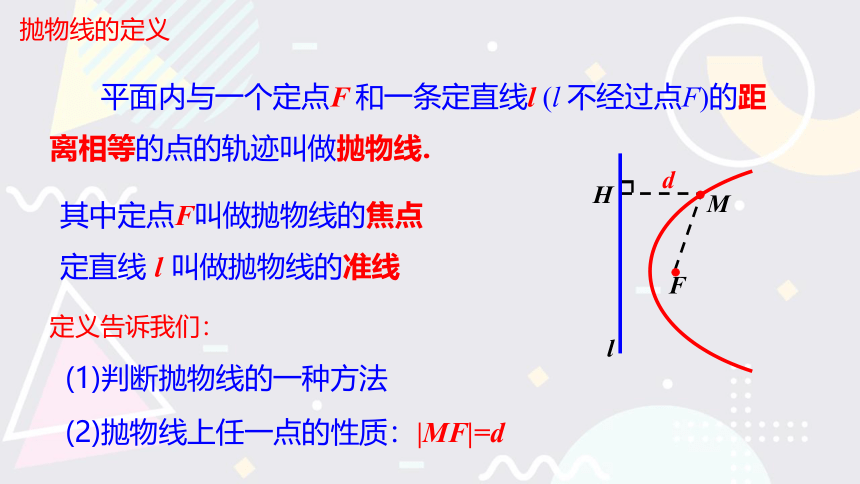
其中定点F叫做抛物线的焦点
定直线 l 叫做抛物线的准线
定义告诉我们:
(1)判断抛物线的一种方法
(2)抛物线上任一点的性质:|MF|=d
抛物线的定义
平面内与一个定点F 和一条定直线l (l 不经过点F)的距离相等的点的轨迹叫做抛物线.
┑
l
F
M
d
H
M
·
F
l
·
e=1
|MF|=d
d 为 M 到 l 的距离
准线
焦点
d
想一想
如果点F在直线l上,满足条件的点的轨迹是抛物线吗?
如何建立直角坐标系?
想一想
探索研究 推出方程
求曲线方程的基本步骤
·
F
L
-1
y
x
O
-2
1
x
y=x2-2x-1
y=x2-2
y=x2
为了给抛物线建立适当的坐标系,看看左边的方程哪一种简单,为什么会简单?启发我们怎样建立坐标系?
┑
l
F
M
d
H
y
O
x
l
F
y
O
M(x, y)
K
H
┑
┑
p
以过F且垂直于l 的直线为x轴,垂足为K.以F,K的中点O为坐标原点建立直角坐标系xOy.
两边平方,整理得
∵ |MF|=d
它表示的抛物线焦点在x轴的正半轴上,焦点坐标是 ,它的准线方程是
其中p为正常数,它的几何意义是:
焦点到准线的距离(焦准距)
方程y2=2px叫做抛物线的标准方程.
抛物线的标准方程:
抛物线的标准方程
抛物线的焦点坐标和准线方程:
关键:确定P的值
反思总结
y
x
o
探究:一条抛物线,由于它在坐标平面内的位置(即:开口方向)不同,方程也不同,所以抛物线的标准方程还有哪些形式?
请你完成课本第131页的表格.
图形 标准方程 焦点坐标 准线方程 焦点位置
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
y2=2px
(p>0)
y2=-2px
(p>0)
x2=2py
(p>0)
x2=-2py
(p>0)
四种抛物线及其标准方程
x轴的
正半轴上
x轴的
负半轴上
y轴的
正半轴上
y轴的
负半轴上
图形 标准方程
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
y2=2px
(p>0)
y2=-2px
(p>0)
x2=2py
(p>0)
x2=-2py
(p>0)
四种抛物线及其标准方程
2.如何根据抛物线的标准方程来判断抛物线的焦点位置及开口方向?
①焦点在一次项字母对应的坐标轴上.
②一次项系数的符号决定了抛物线的开口方向.
1.抛物线的四种标准方程形式上有什么共同特点
左边都是平方项,
右边都是一次项.
+X,x轴正半轴,向右
-X,x轴负半轴,向左
+y,y轴正半轴,向上
-y,y轴负半轴,向下
抛物线焦点位置及开口方向的判断
(以下方程p>0)
▲如何确定各曲线的焦点位置?
抛物线:1.看一次项(X或Y)定焦点
2. 一次项系数正负定开口
椭 圆:看分母大小
双曲线:看符号正负
例1 (1)已知抛物线的标准方程是y2 = 6x,求它的焦点坐标和准线方程;
(2)已知抛物线的焦点坐标是F(0,-2), 求它的标准方程.
解:
课本P133 练习 2
2.求下列抛物线的焦点坐标和准线方程∶
(1)y2=20x; (2)x2=y; (3)2y2+5x=0; (4)x +8y=0.
作业:课本P138 习题3.3 1
全优P116 右边 跟踪训练 4
4.已知抛物线C∶y=mx (m∈R,m≠0))过点P(-1,4),则抛物线C的准线方程为___________________________.
全优P116 右边 跟踪训练 3
3.设抛物线y=2px(p>0)的焦点为F,若F到直线y=x的距离为,则p为( )
A.2 B.4 C.2 D.4
课本P133 练习 1
1.根据下列条件写出抛物线的标准方程∶
(1)焦点是F(3,0);
(2)准线方程是x=;
(3)焦点到准线的距离是2.
作业:课本P138 习题3.3 2
(要写解题过程)
全优P115 右边 预习自测 1
1.抛物线x =y上的一点M到焦点的距离为1,则点M的纵坐标是( )
全优P115 右边 预习自测 2
2.抛物线y2=2px(p>0)上一点M的横坐标为3,且|MF|=2p,则抛物线方程为_________________.
课本P133 练习 3
3.填空.
(1)抛物线y =2px(p>0)上一点M与焦点间的距离是a(),则点 M到准线的距离是____________,点 M 的横坐标是___________________________;
(2)抛物线 y =12x 上与焦点的距离等于9的点的坐标是____________________.
全优P115 左边 预习自测
若点P到直线x=-1的距离比它到点(2,0)的距离小1,则点P的轨迹为( )
A.圆 B.椭圆 C.双曲线 D.抛物线
例2 一种卫星接收天线的轴截面如图所示, 其曲面与轴截面的交线为抛物线. 在轴截面内的卫星波束呈近似平行状态射入形为抛物线的接收天线, 经反射聚集到焦点处. 已知接收天线的口径(直径)为4.8m, 深度为1m. 试建立适当的坐标系, 求抛物线的标准方程和焦点坐标.
y
O
F
x
A
B
y
O
F
x
A
B
例2 一种卫星接收天线的轴截面如图所示, 其曲面与轴截面的交线为抛物线. 在轴截面内的卫星波束呈近似平行状态射入形为抛物线的接收天线, 经反射聚集到焦点处. 已知接收天线的口径(直径)为4.8m, 深度为1m. 试建立适当的坐标系, 求抛物线的标准方程和焦点坐标.
进一步归纳:
本小节结束
F佳
F佳
抛物线及其标准方程
赵州桥
喷泉
探照灯
生活中存在着各种形式的抛物线
500米口径球面射电望远镜:天眼
球在空中运动的轨迹是抛物线。
抛物线到底有怎样的几何特征?
抛物线方程又有什么样的形式呢?
y
x
o
二次函数是开口向上或向下的抛物线。
问题探究:当|MF|=|MH| ,点M的轨迹是什么?
探究?
可以发现,点M随着H运动的过程中,始终|MF|=|MH|,
即点M与点F和定直线l的距离相等.点M生成的轨迹是曲线C的形状.(如图)
M
·
F
l
·
e=1
我们把这样的一条曲线叫做抛物线.
其中定点F叫做抛物线的焦点
定直线 l 叫做抛物线的准线
定义告诉我们:
(1)判断抛物线的一种方法
(2)抛物线上任一点的性质:|MF|=d
抛物线的定义
平面内与一个定点F 和一条定直线l (l 不经过点F)的距离相等的点的轨迹叫做抛物线.
┑
l
F
M
d
H
M
·
F
l
·
e=1
|MF|=d
d 为 M 到 l 的距离
准线
焦点
d
想一想
如果点F在直线l上,满足条件的点的轨迹是抛物线吗?
如何建立直角坐标系?
想一想
探索研究 推出方程
求曲线方程的基本步骤
·
F
L
-1
y
x
O
-2
1
x
y=x2-2x-1
y=x2-2
y=x2
为了给抛物线建立适当的坐标系,看看左边的方程哪一种简单,为什么会简单?启发我们怎样建立坐标系?
┑
l
F
M
d
H
y
O
x
l
F
y
O
M(x, y)
K
H
┑
┑
p
以过F且垂直于l 的直线为x轴,垂足为K.以F,K的中点O为坐标原点建立直角坐标系xOy.
两边平方,整理得
∵ |MF|=d
它表示的抛物线焦点在x轴的正半轴上,焦点坐标是 ,它的准线方程是
其中p为正常数,它的几何意义是:
焦点到准线的距离(焦准距)
方程y2=2px叫做抛物线的标准方程.
抛物线的标准方程:
抛物线的标准方程
抛物线的焦点坐标和准线方程:
关键:确定P的值
反思总结
y
x
o
探究:一条抛物线,由于它在坐标平面内的位置(即:开口方向)不同,方程也不同,所以抛物线的标准方程还有哪些形式?
请你完成课本第131页的表格.
图形 标准方程 焦点坐标 准线方程 焦点位置
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
y2=2px
(p>0)
y2=-2px
(p>0)
x2=2py
(p>0)
x2=-2py
(p>0)
四种抛物线及其标准方程
x轴的
正半轴上
x轴的
负半轴上
y轴的
正半轴上
y轴的
负半轴上
图形 标准方程
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
y2=2px
(p>0)
y2=-2px
(p>0)
x2=2py
(p>0)
x2=-2py
(p>0)
四种抛物线及其标准方程
2.如何根据抛物线的标准方程来判断抛物线的焦点位置及开口方向?
①焦点在一次项字母对应的坐标轴上.
②一次项系数的符号决定了抛物线的开口方向.
1.抛物线的四种标准方程形式上有什么共同特点
左边都是平方项,
右边都是一次项.
+X,x轴正半轴,向右
-X,x轴负半轴,向左
+y,y轴正半轴,向上
-y,y轴负半轴,向下
抛物线焦点位置及开口方向的判断
(以下方程p>0)
▲如何确定各曲线的焦点位置?
抛物线:1.看一次项(X或Y)定焦点
2. 一次项系数正负定开口
椭 圆:看分母大小
双曲线:看符号正负
例1 (1)已知抛物线的标准方程是y2 = 6x,求它的焦点坐标和准线方程;
(2)已知抛物线的焦点坐标是F(0,-2), 求它的标准方程.
解:
课本P133 练习 2
2.求下列抛物线的焦点坐标和准线方程∶
(1)y2=20x; (2)x2=y; (3)2y2+5x=0; (4)x +8y=0.
作业:课本P138 习题3.3 1
全优P116 右边 跟踪训练 4
4.已知抛物线C∶y=mx (m∈R,m≠0))过点P(-1,4),则抛物线C的准线方程为___________________________.
全优P116 右边 跟踪训练 3
3.设抛物线y=2px(p>0)的焦点为F,若F到直线y=x的距离为,则p为( )
A.2 B.4 C.2 D.4
课本P133 练习 1
1.根据下列条件写出抛物线的标准方程∶
(1)焦点是F(3,0);
(2)准线方程是x=;
(3)焦点到准线的距离是2.
作业:课本P138 习题3.3 2
(要写解题过程)
全优P115 右边 预习自测 1
1.抛物线x =y上的一点M到焦点的距离为1,则点M的纵坐标是( )
全优P115 右边 预习自测 2
2.抛物线y2=2px(p>0)上一点M的横坐标为3,且|MF|=2p,则抛物线方程为_________________.
课本P133 练习 3
3.填空.
(1)抛物线y =2px(p>0)上一点M与焦点间的距离是a(),则点 M到准线的距离是____________,点 M 的横坐标是___________________________;
(2)抛物线 y =12x 上与焦点的距离等于9的点的坐标是____________________.
全优P115 左边 预习自测
若点P到直线x=-1的距离比它到点(2,0)的距离小1,则点P的轨迹为( )
A.圆 B.椭圆 C.双曲线 D.抛物线
例2 一种卫星接收天线的轴截面如图所示, 其曲面与轴截面的交线为抛物线. 在轴截面内的卫星波束呈近似平行状态射入形为抛物线的接收天线, 经反射聚集到焦点处. 已知接收天线的口径(直径)为4.8m, 深度为1m. 试建立适当的坐标系, 求抛物线的标准方程和焦点坐标.
y
O
F
x
A
B
y
O
F
x
A
B
例2 一种卫星接收天线的轴截面如图所示, 其曲面与轴截面的交线为抛物线. 在轴截面内的卫星波束呈近似平行状态射入形为抛物线的接收天线, 经反射聚集到焦点处. 已知接收天线的口径(直径)为4.8m, 深度为1m. 试建立适当的坐标系, 求抛物线的标准方程和焦点坐标.
进一步归纳:
本小节结束
F佳
