2021-2022学年京改版八年级上册第十二章 三角形课后培优练习 (word版含答案)
文档属性
| 名称 | 2021-2022学年京改版八年级上册第十二章 三角形课后培优练习 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 338.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-25 17:09:06 | ||
图片预览



文档简介
第十二章 三角形
一、单选题
1.若△ABC的∠A=60°,且∠B:∠C=2:1,那么∠B的度数为 ( )
A.40° B.80° C.60° D.120°
2.如果一个直角三角形的两边分别是6,8,那么斜边上的中线是( )
A.4 B.5 C.4或5 D.3或5
3.下列叙述中错误的是( )
A.能够完全重合的图形称为全等图形
B.全等图形的形状和大小都相同
C.所有正方形都是全等图形
D.形状和大小都相同的两个图形是全等图形
4.国有银行,是指由国家(财政部、中央汇金公司)直接管控的大型银行.下面是我国其中五个国有银行的图标,分别是中国工商银行、交通银行、中国农业银行、中国银行、中国建设银行,其中轴对称图形有( )
A.2个 B.3个 C.4个 D.5个
5.在△ABC中,AB=1,AC=2,BC=,则该三角形为( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰直角三角形
6.如图,已知∠MON及其边上一点A,以点A为圆心,AO长为半径画弧,分别交OM,ON于点B和C,再以点C为圆心,AC长为半径画弧,恰好经过点B,错误的结论是( ).
A. B.∠OCB=90° C.∠MON=30° D.OC=2BC
7.若一个等腰三角形的两边长分别为 4,5,则这个等腰三角形的周长为( )
A.13 B.14 C.13 或 14 D.8或 10
8.如图,,则的长是( )
A. B. C. D.
9.有一个边长为40cm的正方形洞口,要用一个圆盖去盖住这个洞口,那么圆盖的直径至少应为( )
A.40cm B.20cm C.40cm D.40cm
10.已知三条线的比如下,可以组成三角形的是( )
A.5:20:30 B.10:20:30
C.15:15:30 D.20:30:30
11.如图所示,四边形ABCD是凸四边形,AB=2,BC=4,CD=7,则线段AD的取值范围为( )
A.0<AD<7 B.2<AD<7 C.0<AD<13 D.1<AD<13
12.下列条件能组成全等三角形的是 ( )
A.有一个顶角相等的两个等腰三角形
B.有一边相等的两个等边三角形
C.有两腰对应相等的两个等腰三角形
D.底边相等的两个等腰三角形
13.将直角三角形的三条边长同时缩小为原来的一半,所得到的三角形为 ( )
A.直角三角形 B.锐角三角形 C.等腰三角形 D.钝角三角形
14.小华先向东走了16m后,接着向北走了12m,此时小华离出发点的距离是( )
A.28 m B.16 m C.20 m D.12 m
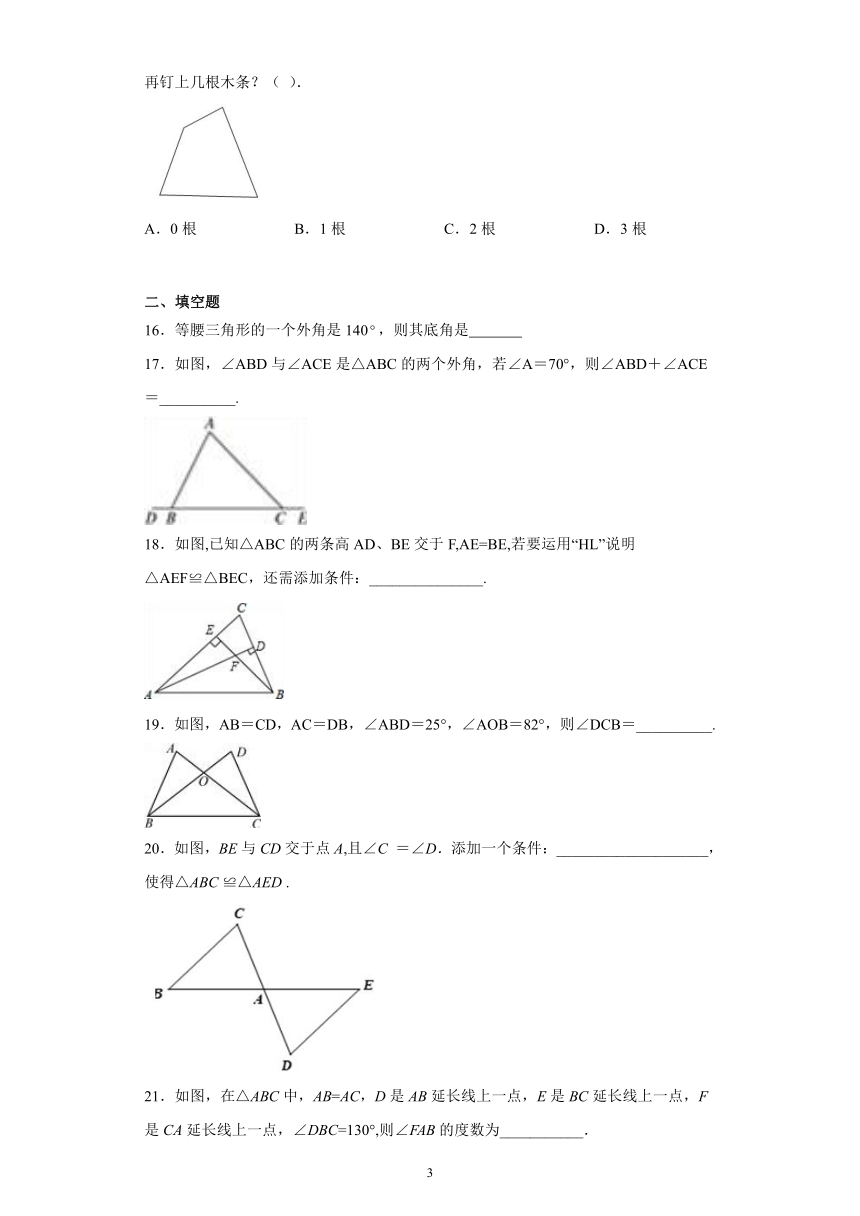
15.王师傅用4根木条钉成一个四边形木架,如图.要使这个木架不变形,他至少还要再钉上几根木条?( ).
A.0根 B.1根 C.2根 D.3根
二、填空题
16.等腰三角形的一个外角是140,则其底角是
17.如图,∠ABD与∠ACE是△ABC的两个外角,若∠A=70°,则∠ABD+∠ACE=__________.
18.如图,已知△ABC的两条高AD、BE交于F,AE=BE,若要运用“HL”说明△AEF≌△BEC,还需添加条件:_______________.
19.如图,AB=CD,AC=DB,∠ABD=25°,∠AOB=82°,则∠DCB=__________.
20.如图,BE与CD交于点A,且∠C =∠D.添加一个条件:____________________,使得△ABC ≌△AED .
21.如图,在△ABC中,AB=AC,D是AB延长线上一点,E是BC延长线上一点,F是CA延长线上一点,∠DBC=130°,则∠FAB的度数为___________.
三、解答题
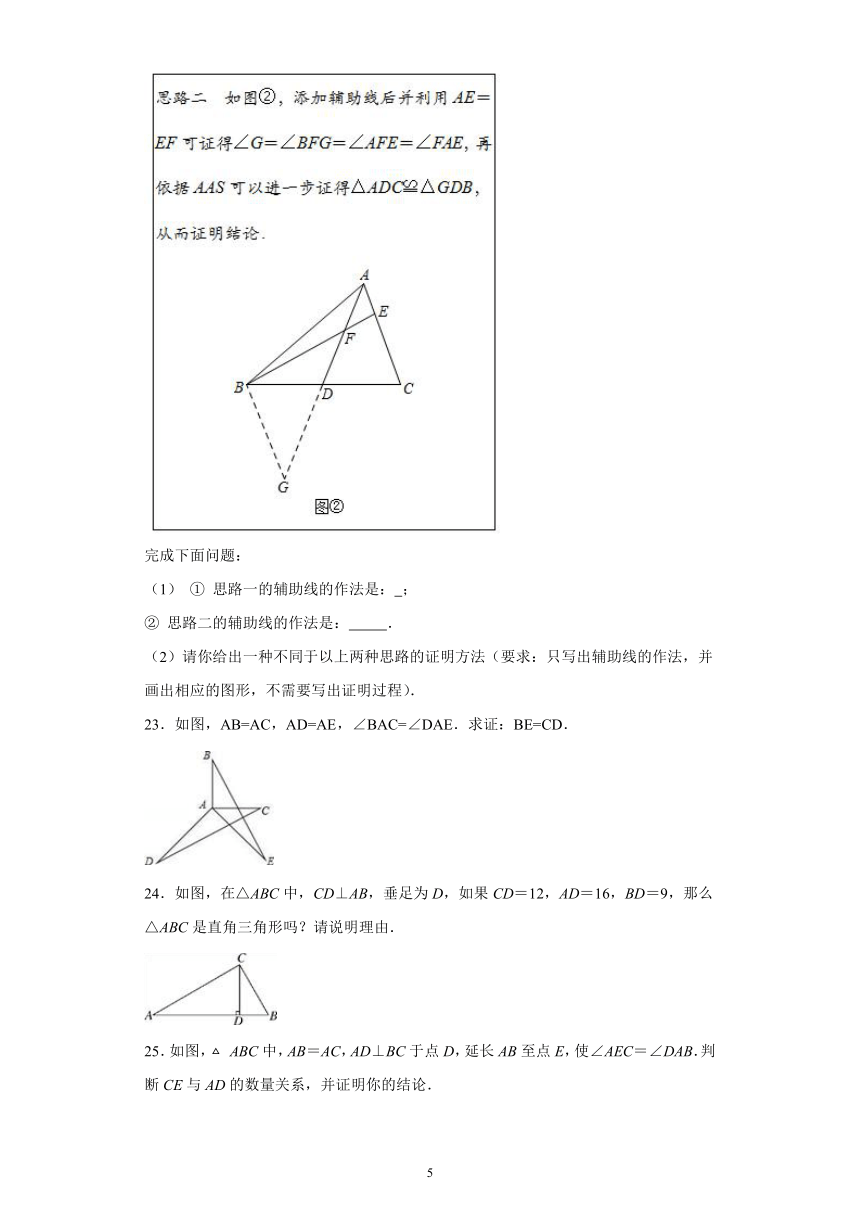
22.阅读下面材料:
数学课上,老师给出了如下问题:
如图,AD为△ABC中线,点E在AC上,BE交AD于点F,AE=EF.求证:AC=BF.
经过讨论,同学们得到以下两种思路:
完成下面问题:
(1) ① 思路一的辅助线的作法是: ;
② 思路二的辅助线的作法是: .
(2)请你给出一种不同于以上两种思路的证明方法(要求:只写出辅助线的作法,并画出相应的图形,不需要写出证明过程).
23.如图,AB=AC,AD=AE,∠BAC=∠DAE.求证:BE=CD.
24.如图,在△ABC中,CD⊥AB,垂足为D,如果CD=12,AD=16,BD=9,那么△ABC是直角三角形吗?请说明理由.
25.如图, ABC中,AB=AC,AD⊥BC于点D,延长AB至点E,使∠AEC=∠DAB.判断CE与AD的数量关系,并证明你的结论.
26.如图,在平面直角坐标系中,O为坐标原点,△ABC的边BC在x轴上,A,C两点的坐标分别为A(0,m),C(n,0),B(﹣5,0),且(n﹣3)2+ =0.一动点P从点B出发,以每秒2单位长度的速度沿射线BO匀速运动,设点P运动的时间为ts.
(1)求A,C两点的坐标;
(2)连接PA,若△PAB为等腰三角形,求点P的坐标;
(3)当点P在线段BO上运动时,在y轴上是否存在点Q,使△POQ与△AOC全等?若存在,请求出t的值并直接写出点Q的坐标;若不存在,请说明理由.
参考答案
1.B
解:∵△ABC的∠A=60°,
∴∠B+∠C=120°,
∵∠B:∠C=2:1,
∴∠B=,
故选:B.
2.C
当一个直角三角形的两直角边分别是6,8时,
由勾股定理得,斜边==10,则斜边上的中线=×10=5,
当8是斜边时,斜边上的中线是4,
故选C.
3.C
解:A.能够重合的图形称为全等图形,说法正确,故本选项错误;
B.全等图形的形状和大小都相同,说法正确,故本选项错误;
C.所有正方形不一定都是全等图形,说法错误,故本选项正确;
D.形状和大小都相同的两个图形是全等图形,说法正确,故本选项错误;
故选C.
4.B
解:图标是轴对称图形有中国工商银行、中国农业银行、中国银行,一共有3个轴对称图形
故选:B.
5.B
解:在△ABC中,AB=1,AC=2,BC=.∵,∴△ABC是直角三角形.
故选B.
6.D
过C作CD⊥OB,垂足为D,如图所示,
∵S△OAC=,S△ABC=,OA=AB,
∴,故选项A正确,不符合题意;
∵OA=AC=AB=BC,
∴BC=OB,
∴△OCB是直角三角形,∠OCB=90°,故选项B正确,不符合题意;
在Rt△OCB中,∠OCB=90°,BC=OB,
∴∠COB=30°,即∠MON=30°,故选项C正确,不符合题意;
∵OB=2BC,OB>OC,
∴OC≠2BC,故选项D错误,符合题意.
故选:D.
7.C
分两种情况讨论:
①若4为腰长,5为底边长.
由于4+4>5,则符合三角形的两边之和大于第三边,周长为:4+4+5=13;
②若5为腰长,4为底边长.
由于5+5>4,则符合三角形的两边之和大于第三边,周长为:5+5+4=14.
综上所述:这个等腰三角形的周长为:13或14.
故选C.
8.D
解:∵△ABC≌△CDA,
∴AD=BC=8cm.
故选D.
9.C
解:根据题意,知圆盖的直径至少应为正方形的对角线的长;再根据勾股定理,得圆盖的直径至少应为:=.故选C.
10.D
设一份为1,根据三角形的三边关系可得:选项A,5+20<30,不能组成三角形;选项B,10+20=30,不能组成三角形;选项C,15+15=30,不能组成三角形;选项D,20+30>30,能组成三角形.故选D.
11.D
连接AC,
∵AB=2,BC=4,
在△ABC中,根据三角形的三边关系,4 2∴ 6< AC< 2,1在△ACD中,根据三角形的三边关系,得CD AC∴1故选:D.
12.B
A选项:两个顶角相等,但两个三角形的腰不一定相等,故不能判断两个三角形全等;
B选项:根据SSS判断两个三角形全等,故能判断两个三角形全等;
C选项:只有两腰相等,但两腰夹角不一定相等,故不能判定两三角形全等;
D选项:底边相等的两个等腰三角形,只已知一条边相等,故不能判定两三角形全等.
13.A
直角三角形的三条边长同时缩小为原来的一半,只是三角形的大小发生改变,三角形的形状不变,故选A.
14.C
根据勾股定理可得小华离出发点的距离是m,故选C.
15.B
三角形具有稳定性,连接一条对角线,即可得到两个三角形,故选B
16.70°或40°
解:当140°外角为顶角的外角时,则其顶角为:40°,则其底角为:(180°-40°)÷2 =70°,当140°外角为底角的外角时,则其底角为:180°﹣140°=40°.故答案为70°或40°.
点睛:本题主要考查等腰三角形的性质和三角形内角和定理的应用,掌握等腰三角形的两底角相等和三角形三个内角的和为180°是解题的关键.
17.250°
试题解析:
故答案为
18.AF=BC
HL指的是斜边、直角边定理,只能添加两条斜边相等,即AF=BC.
19.66°
试题解析:在△ABC和△DCB中,
∴△ABC≌△DCB(SSS),
∴∠ACB=∠DBC,∠ABC=∠DCB,
故答案为
20.AC=AD
∵∠C =∠D,∠BAC=∠EAD,
∴当AC=AD时,依据ASA可得,△ABC≌△AED.
故答案为:AC=AD(答案不唯一).
21.
∵,,
∴,
∵AB=AC,
∴,
∵∠FAB是△ABC的一个外角,
∴,
故答案为:.
22.(1) ①延长AD至点G,使DG=AD,连接BG;②作BG=BF交AD的延长线于点G;(2)见解析
解:(1)①如图①,延长AD至点G,使DG=AD,连接BG,
∵AD为△ABC中线,
∴BD=CD,
在△ADC和△GDB中,
∵AD=GD,∠ADC=∠GDB,CD=BD,
∴△ADC≌△GDB(SAS),
∴AC=BG,
∵AE=EF,
∴∠CAD=∠EFA,
∵∠BFG=∠G,∠G=∠CAD,
∴∠G=∠BFG,
∴BG=BF,
∴AC=BF;
②如图②,作BG=BF交AD的延长线于点G,
∵BG=BF,
∴∠G=∠BFG,
∵AE=EF,
∴∠EAF=∠EFA,
∵∠EFA=∠BFG,
∴∠G=∠EAF,
在△ADC和△GDB中,
∵∠CAD=∠G,∠ADC=∠GDB,CD=BD,
∴△ADC≌△GDB(AAS),
∴AC=BG,
∴AC=BF;
(2)如图,过点B作BG∥AC交AD延长线于点G,
则∠G=∠CAD,
∵AD为△ABC中线,
∴BD=CD,
在△ADC和△GDB中,
∵∠CAD=∠G,∠ADC=∠GDB,CD=BD,
∴△ADC≌△GDB(AAS),
∴AC=BG,
∵AE=EF,
∴∠CAD=∠EFA,
∵∠BFG=∠EFA,∠G=∠CAD,
∴∠G=∠BFG,
∴BG=BF,
∴AC=BF.
23.证明见解析
∵∠BAC=∠DAE,
∴∠BAC+∠CAE=∠DAE+∠CAE,
∴∠BAE=∠CAD,
∵AB=AC,AD=AE,
∴△BAE≌△CAD(SAS),
∴BE=CD.
24.△ABC是直角三角形.
解:是.理由如下:
∵CD⊥AB,CD=12,AD=16,BD=9,∴AC2=CD2+AD2=400.又∵CD⊥AB,AD=16,BD=9,∴BC2=CD2+BD2=225.∵AB=AD+BD=25,∴AB2=625,∴AC2+BC2=625=AB2,∴△ABC是直角三角形.
25.CE=2AD,证明详见解析
解:CE=2AD;
理由:延长AD至点N使DN=AD,AN交CE于点M,连接CN,
∵∠DAB=∠AEC,
∴MA=ME,
∵AB=AC,AD⊥BC,
∴∠CAD=∠DAB,BD=CD,∠1=∠2=90°.
∴ABD≌NCD(AAS),
∴∠N=∠DAB.
∴CN∥AE.
∴∠3=∠AEC.
∴∠3=∠N.
∴MC=MN,
∴CE=MC+ME
=MN+MA
=AN
=2AD.
26.(1)A(0,4),C(3,0);(2)(﹣0.9,0)或(5,0);( ﹣5,0);(3)存在,当t=1秒,点Q的坐标为(0,4)或(0,﹣4);当t=秒,点Q的坐标为(0,3)或(0,﹣3)
(1)∵(n﹣3)2+=0,
∴n﹣3=0,3m﹣12=0,
解得,n=3,m=4,
∴点A的坐标为(0,4),点C的坐标为(3,0);
(2)由勾股定理得,AB==,
当BA=BP时,点P的坐标为(﹣5,0);
当AB=AP时,点P的坐标(5,0);
当PA=PB时,设PA=x,则OP=5﹣x,
在Rt△AOP中,AP2=OP2+OA2,即x2=(5﹣x)2+42,
解得,x=4.1,
则OP=0.9,
∴点P的坐标(﹣0.9,0);
综上所述,△PAB为等腰三角形,点P的坐标为(﹣0.9,0)或(5,0);( ﹣5,0);
(3)当△QOP≌△AOC时,OP=OC=3,OQ=OA=4,
∴BP=2,
则t=1秒,点Q的坐标为(0,4)或(0,﹣4);
当△POQ≌△AOC时,OP=OA=4,OQ=OC=3,
则t=秒,点Q的坐标为(0,3)或(0,﹣3).
一、单选题
1.若△ABC的∠A=60°,且∠B:∠C=2:1,那么∠B的度数为 ( )
A.40° B.80° C.60° D.120°
2.如果一个直角三角形的两边分别是6,8,那么斜边上的中线是( )
A.4 B.5 C.4或5 D.3或5
3.下列叙述中错误的是( )
A.能够完全重合的图形称为全等图形
B.全等图形的形状和大小都相同
C.所有正方形都是全等图形
D.形状和大小都相同的两个图形是全等图形
4.国有银行,是指由国家(财政部、中央汇金公司)直接管控的大型银行.下面是我国其中五个国有银行的图标,分别是中国工商银行、交通银行、中国农业银行、中国银行、中国建设银行,其中轴对称图形有( )
A.2个 B.3个 C.4个 D.5个
5.在△ABC中,AB=1,AC=2,BC=,则该三角形为( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰直角三角形
6.如图,已知∠MON及其边上一点A,以点A为圆心,AO长为半径画弧,分别交OM,ON于点B和C,再以点C为圆心,AC长为半径画弧,恰好经过点B,错误的结论是( ).
A. B.∠OCB=90° C.∠MON=30° D.OC=2BC
7.若一个等腰三角形的两边长分别为 4,5,则这个等腰三角形的周长为( )
A.13 B.14 C.13 或 14 D.8或 10
8.如图,,则的长是( )
A. B. C. D.
9.有一个边长为40cm的正方形洞口,要用一个圆盖去盖住这个洞口,那么圆盖的直径至少应为( )
A.40cm B.20cm C.40cm D.40cm
10.已知三条线的比如下,可以组成三角形的是( )
A.5:20:30 B.10:20:30
C.15:15:30 D.20:30:30
11.如图所示,四边形ABCD是凸四边形,AB=2,BC=4,CD=7,则线段AD的取值范围为( )
A.0<AD<7 B.2<AD<7 C.0<AD<13 D.1<AD<13
12.下列条件能组成全等三角形的是 ( )
A.有一个顶角相等的两个等腰三角形
B.有一边相等的两个等边三角形
C.有两腰对应相等的两个等腰三角形
D.底边相等的两个等腰三角形
13.将直角三角形的三条边长同时缩小为原来的一半,所得到的三角形为 ( )
A.直角三角形 B.锐角三角形 C.等腰三角形 D.钝角三角形
14.小华先向东走了16m后,接着向北走了12m,此时小华离出发点的距离是( )
A.28 m B.16 m C.20 m D.12 m
15.王师傅用4根木条钉成一个四边形木架,如图.要使这个木架不变形,他至少还要再钉上几根木条?( ).
A.0根 B.1根 C.2根 D.3根
二、填空题
16.等腰三角形的一个外角是140,则其底角是
17.如图,∠ABD与∠ACE是△ABC的两个外角,若∠A=70°,则∠ABD+∠ACE=__________.
18.如图,已知△ABC的两条高AD、BE交于F,AE=BE,若要运用“HL”说明△AEF≌△BEC,还需添加条件:_______________.
19.如图,AB=CD,AC=DB,∠ABD=25°,∠AOB=82°,则∠DCB=__________.
20.如图,BE与CD交于点A,且∠C =∠D.添加一个条件:____________________,使得△ABC ≌△AED .
21.如图,在△ABC中,AB=AC,D是AB延长线上一点,E是BC延长线上一点,F是CA延长线上一点,∠DBC=130°,则∠FAB的度数为___________.
三、解答题
22.阅读下面材料:
数学课上,老师给出了如下问题:
如图,AD为△ABC中线,点E在AC上,BE交AD于点F,AE=EF.求证:AC=BF.
经过讨论,同学们得到以下两种思路:
完成下面问题:
(1) ① 思路一的辅助线的作法是: ;
② 思路二的辅助线的作法是: .
(2)请你给出一种不同于以上两种思路的证明方法(要求:只写出辅助线的作法,并画出相应的图形,不需要写出证明过程).
23.如图,AB=AC,AD=AE,∠BAC=∠DAE.求证:BE=CD.
24.如图,在△ABC中,CD⊥AB,垂足为D,如果CD=12,AD=16,BD=9,那么△ABC是直角三角形吗?请说明理由.
25.如图, ABC中,AB=AC,AD⊥BC于点D,延长AB至点E,使∠AEC=∠DAB.判断CE与AD的数量关系,并证明你的结论.
26.如图,在平面直角坐标系中,O为坐标原点,△ABC的边BC在x轴上,A,C两点的坐标分别为A(0,m),C(n,0),B(﹣5,0),且(n﹣3)2+ =0.一动点P从点B出发,以每秒2单位长度的速度沿射线BO匀速运动,设点P运动的时间为ts.
(1)求A,C两点的坐标;
(2)连接PA,若△PAB为等腰三角形,求点P的坐标;
(3)当点P在线段BO上运动时,在y轴上是否存在点Q,使△POQ与△AOC全等?若存在,请求出t的值并直接写出点Q的坐标;若不存在,请说明理由.
参考答案
1.B
解:∵△ABC的∠A=60°,
∴∠B+∠C=120°,
∵∠B:∠C=2:1,
∴∠B=,
故选:B.
2.C
当一个直角三角形的两直角边分别是6,8时,
由勾股定理得,斜边==10,则斜边上的中线=×10=5,
当8是斜边时,斜边上的中线是4,
故选C.
3.C
解:A.能够重合的图形称为全等图形,说法正确,故本选项错误;
B.全等图形的形状和大小都相同,说法正确,故本选项错误;
C.所有正方形不一定都是全等图形,说法错误,故本选项正确;
D.形状和大小都相同的两个图形是全等图形,说法正确,故本选项错误;
故选C.
4.B
解:图标是轴对称图形有中国工商银行、中国农业银行、中国银行,一共有3个轴对称图形
故选:B.
5.B
解:在△ABC中,AB=1,AC=2,BC=.∵,∴△ABC是直角三角形.
故选B.
6.D
过C作CD⊥OB,垂足为D,如图所示,
∵S△OAC=,S△ABC=,OA=AB,
∴,故选项A正确,不符合题意;
∵OA=AC=AB=BC,
∴BC=OB,
∴△OCB是直角三角形,∠OCB=90°,故选项B正确,不符合题意;
在Rt△OCB中,∠OCB=90°,BC=OB,
∴∠COB=30°,即∠MON=30°,故选项C正确,不符合题意;
∵OB=2BC,OB>OC,
∴OC≠2BC,故选项D错误,符合题意.
故选:D.
7.C
分两种情况讨论:
①若4为腰长,5为底边长.
由于4+4>5,则符合三角形的两边之和大于第三边,周长为:4+4+5=13;
②若5为腰长,4为底边长.
由于5+5>4,则符合三角形的两边之和大于第三边,周长为:5+5+4=14.
综上所述:这个等腰三角形的周长为:13或14.
故选C.
8.D
解:∵△ABC≌△CDA,
∴AD=BC=8cm.
故选D.
9.C
解:根据题意,知圆盖的直径至少应为正方形的对角线的长;再根据勾股定理,得圆盖的直径至少应为:=.故选C.
10.D
设一份为1,根据三角形的三边关系可得:选项A,5+20<30,不能组成三角形;选项B,10+20=30,不能组成三角形;选项C,15+15=30,不能组成三角形;选项D,20+30>30,能组成三角形.故选D.
11.D
连接AC,
∵AB=2,BC=4,
在△ABC中,根据三角形的三边关系,4 2
12.B
A选项:两个顶角相等,但两个三角形的腰不一定相等,故不能判断两个三角形全等;
B选项:根据SSS判断两个三角形全等,故能判断两个三角形全等;
C选项:只有两腰相等,但两腰夹角不一定相等,故不能判定两三角形全等;
D选项:底边相等的两个等腰三角形,只已知一条边相等,故不能判定两三角形全等.
13.A
直角三角形的三条边长同时缩小为原来的一半,只是三角形的大小发生改变,三角形的形状不变,故选A.
14.C
根据勾股定理可得小华离出发点的距离是m,故选C.
15.B
三角形具有稳定性,连接一条对角线,即可得到两个三角形,故选B
16.70°或40°
解:当140°外角为顶角的外角时,则其顶角为:40°,则其底角为:(180°-40°)÷2 =70°,当140°外角为底角的外角时,则其底角为:180°﹣140°=40°.故答案为70°或40°.
点睛:本题主要考查等腰三角形的性质和三角形内角和定理的应用,掌握等腰三角形的两底角相等和三角形三个内角的和为180°是解题的关键.
17.250°
试题解析:
故答案为
18.AF=BC
HL指的是斜边、直角边定理,只能添加两条斜边相等,即AF=BC.
19.66°
试题解析:在△ABC和△DCB中,
∴△ABC≌△DCB(SSS),
∴∠ACB=∠DBC,∠ABC=∠DCB,
故答案为
20.AC=AD
∵∠C =∠D,∠BAC=∠EAD,
∴当AC=AD时,依据ASA可得,△ABC≌△AED.
故答案为:AC=AD(答案不唯一).
21.
∵,,
∴,
∵AB=AC,
∴,
∵∠FAB是△ABC的一个外角,
∴,
故答案为:.
22.(1) ①延长AD至点G,使DG=AD,连接BG;②作BG=BF交AD的延长线于点G;(2)见解析
解:(1)①如图①,延长AD至点G,使DG=AD,连接BG,
∵AD为△ABC中线,
∴BD=CD,
在△ADC和△GDB中,
∵AD=GD,∠ADC=∠GDB,CD=BD,
∴△ADC≌△GDB(SAS),
∴AC=BG,
∵AE=EF,
∴∠CAD=∠EFA,
∵∠BFG=∠G,∠G=∠CAD,
∴∠G=∠BFG,
∴BG=BF,
∴AC=BF;
②如图②,作BG=BF交AD的延长线于点G,
∵BG=BF,
∴∠G=∠BFG,
∵AE=EF,
∴∠EAF=∠EFA,
∵∠EFA=∠BFG,
∴∠G=∠EAF,
在△ADC和△GDB中,
∵∠CAD=∠G,∠ADC=∠GDB,CD=BD,
∴△ADC≌△GDB(AAS),
∴AC=BG,
∴AC=BF;
(2)如图,过点B作BG∥AC交AD延长线于点G,
则∠G=∠CAD,
∵AD为△ABC中线,
∴BD=CD,
在△ADC和△GDB中,
∵∠CAD=∠G,∠ADC=∠GDB,CD=BD,
∴△ADC≌△GDB(AAS),
∴AC=BG,
∵AE=EF,
∴∠CAD=∠EFA,
∵∠BFG=∠EFA,∠G=∠CAD,
∴∠G=∠BFG,
∴BG=BF,
∴AC=BF.
23.证明见解析
∵∠BAC=∠DAE,
∴∠BAC+∠CAE=∠DAE+∠CAE,
∴∠BAE=∠CAD,
∵AB=AC,AD=AE,
∴△BAE≌△CAD(SAS),
∴BE=CD.
24.△ABC是直角三角形.
解:是.理由如下:
∵CD⊥AB,CD=12,AD=16,BD=9,∴AC2=CD2+AD2=400.又∵CD⊥AB,AD=16,BD=9,∴BC2=CD2+BD2=225.∵AB=AD+BD=25,∴AB2=625,∴AC2+BC2=625=AB2,∴△ABC是直角三角形.
25.CE=2AD,证明详见解析
解:CE=2AD;
理由:延长AD至点N使DN=AD,AN交CE于点M,连接CN,
∵∠DAB=∠AEC,
∴MA=ME,
∵AB=AC,AD⊥BC,
∴∠CAD=∠DAB,BD=CD,∠1=∠2=90°.
∴ABD≌NCD(AAS),
∴∠N=∠DAB.
∴CN∥AE.
∴∠3=∠AEC.
∴∠3=∠N.
∴MC=MN,
∴CE=MC+ME
=MN+MA
=AN
=2AD.
26.(1)A(0,4),C(3,0);(2)(﹣0.9,0)或(5,0);( ﹣5,0);(3)存在,当t=1秒,点Q的坐标为(0,4)或(0,﹣4);当t=秒,点Q的坐标为(0,3)或(0,﹣3)
(1)∵(n﹣3)2+=0,
∴n﹣3=0,3m﹣12=0,
解得,n=3,m=4,
∴点A的坐标为(0,4),点C的坐标为(3,0);
(2)由勾股定理得,AB==,
当BA=BP时,点P的坐标为(﹣5,0);
当AB=AP时,点P的坐标(5,0);
当PA=PB时,设PA=x,则OP=5﹣x,
在Rt△AOP中,AP2=OP2+OA2,即x2=(5﹣x)2+42,
解得,x=4.1,
则OP=0.9,
∴点P的坐标(﹣0.9,0);
综上所述,△PAB为等腰三角形,点P的坐标为(﹣0.9,0)或(5,0);( ﹣5,0);
(3)当△QOP≌△AOC时,OP=OC=3,OQ=OA=4,
∴BP=2,
则t=1秒,点Q的坐标为(0,4)或(0,﹣4);
当△POQ≌△AOC时,OP=OA=4,OQ=OC=3,
则t=秒,点Q的坐标为(0,3)或(0,﹣3).
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
