课件--函数的奇偶性

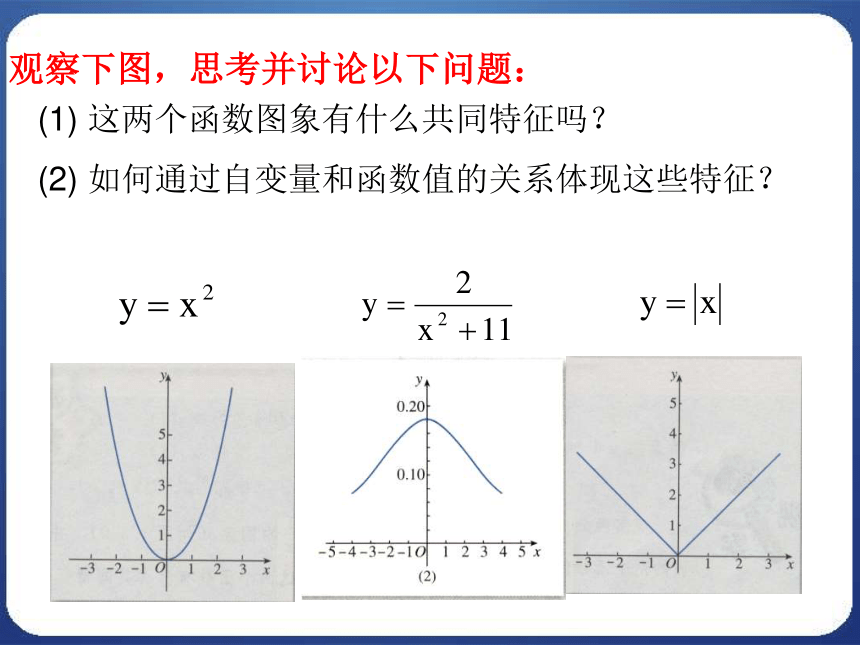
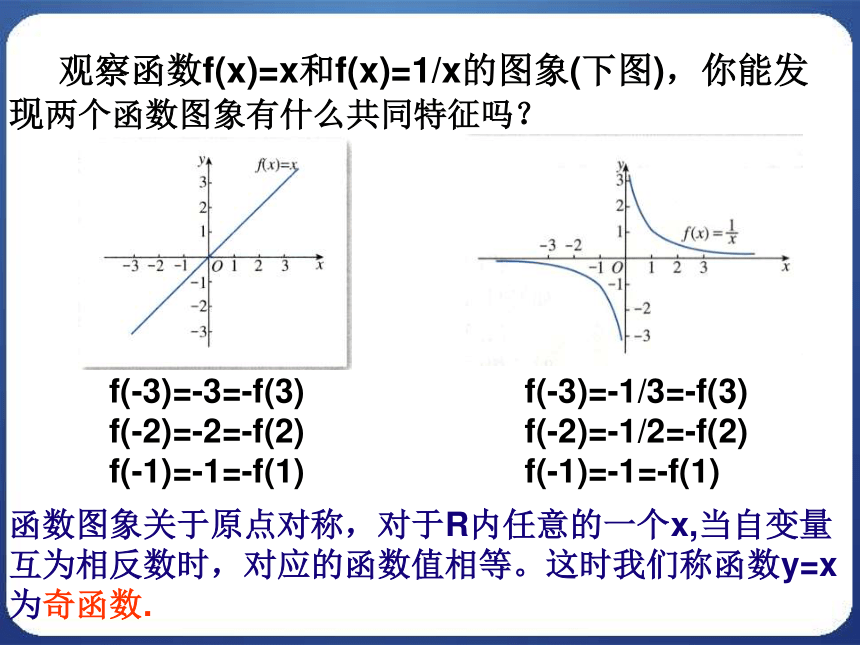
课件13张PPT。1.3.2函数的奇偶性偶函数的定义 一般地，对于函数f(x)的定义域内的任意一个x，都有f(－x)=f(x)，那么f(x)就叫做偶函数． 偶函数的图像关于y轴对称 观察函数f(x)=x和f(x)=1/x的图象(下图)，你能发现两个函数图象有什么共同特征吗？f(-3)=-3=-f(3) f(-2)=-2=-f(2) f(-1)=-1=-f(1)函数图象关于原点对称，对于R内任意的一个x,当自变量互为相反数时，对应的函数值相等。这时我们称函数y=x为奇函数.f(-3)=-1/3=-f(3) f(-2)=-1/2=-f(2) f(-1)=-1=-f(1)奇函数的定义 一般地，对于函数f(x)的定义域内的任意一个x，都有f(-x)=-f(x)，那么f(x)就叫做奇函数． 如果一个函数f(x)是奇函数或偶函数，那么我们就说函数f(x)具有奇偶性.
奇函数的图像关于原点对称思考讨论题：
思考一：奇偶函数的图像有什么特点？如果函数满足该特点，能否说明函数具有奇偶性？
思考二：函数 是偶函数吗？说明奇偶函数的定义域应该满足什么条件？
思考三：如何判断函数的奇偶性，步骤如何？
思考四：若 为偶函数， 为偶函数，则函数 也是偶函数吗？反之成立吗？思考一：奇偶函数的图像有什么特点？如果函数满足该特点，能否说明函数具有奇偶性？ 注意：
一个函数为奇函数 它的图象关于原点对称
一个函数为偶函数 它的图象关于y轴对称思考二：函数 是偶函数吗？说明奇偶函数的定义域应该满足什么条件？练习1、判断下列定义域区间是否关于原点对称
（1）
（2）
（3）
（4） 或
（5） 且思考三：如何判断函数的奇偶性，步骤如何？判断或证明函数单调性的步骤：1、判断函数的定义域是否关于原点对称2、判断 和 的关系3、写出结论练习2、判断下列函数的奇偶性（1）
（2）
（3）
（4）
（5）思考四：若 为偶函数， 为偶函数，则函数 也是偶函数吗？反之成立吗？课堂练习判断下列函数的奇偶性：本课小结1、两个定义：对于f(x)定义域内的任意一个x,
如果都有f(－x)=-f(x) f(x)为奇函数
如果都有f(－x)=f(x) f(x)为偶函数 2、两个性质：
一个函数为奇函数 它的图象关于原点对称
一个函数为偶函数 它的图象关于y轴对称