2022年广东省普通高中学业水平考试数学模拟卷五(Word含答案解析)
文档属性
| 名称 | 2022年广东省普通高中学业水平考试数学模拟卷五(Word含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 386.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 17:00:17 | ||
图片预览




文档简介
2022年广东高中数学学业水平考试模拟卷五
班级:___________姓名:___________座号:___________成绩:___________
一、单选题
1.若全集,集合,则( )
A. B. C. D.
2.已知是定义在上的奇函数,且当时,,则的值为
A. B. C. D.
3.设,,,则( )
A. B.
C. D.
4.下列等式成立的是( )
A. B.
C. D.
5.用一段长为36米的篱笆围成一个一边靠墙的矩形菜园.已知墙长20米,则菜园面积的最大值是( )
A.144 B.160 C.162 D.180
6.函数的零点所在的区间为( )
A. B.
C. D.
7.已知球的表面积为,则该球的体积为
A. B. C. D.
8.对于不同的直线l、、及平面,下列命题中错误的是
A.若,,则 B.若,,则
C.若,,则 D.若,,则
9.已知直线,与互相垂直,则的值是
A. B.或 C. D.或
10.已知点在圆的内部,则( )
A. B.
C. D.
11.某班有学生40人,现用系统抽样的方法,从中抽取一个容量为4的样本,已知样本中学生的座位号分别为4,,24,34,那么的值应是( )
A.12 B.13 C.14 D.15
12.我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为( )
A.134石 B.169石 C.338石 D.1365石
13.某人连续投篮两次,事件“至少投中一次”的互斥事件是( )
A.恰有一次投中 B.至多投中一次 C.两次都中 D.两次都不中
14.将函数的图象上所有点的横坐标缩短到原来的(纵坐标不变),所得图象对应的表达式为( )
A. B.
C. D.
15.已知向量,若∥,则的值等于( )
A. B. C.1 D.
二、填空题
16.,则的等比中项为_________.
17.不等式的解集是,则______.
18.给出下列四个命题:
①若a>b>0,则; ②若a>b>0,则; ③若a>b>0,则;
④若a>0,b>0,且a+b=1,则的最小值为4
其中正确命题的序号是____.(把你认为正确命题的序号都填上)
19.对于函数(),给出下列判断:
①当时,函数为奇函数;
②函数的图象关于点对称;
③当,时,函数的最小值为1.
其中正确的判断是_______.
三、解答题
20.某商店以6元千克的价格购进某种干果1140千克,并对其进行筛选分成甲级干果与乙级干果后同时开始销售.这批干果销售结束后,店主从销售统计中发现:甲级干果与乙级干果在销售过程中每天都有销量,且在同一天卖完;甲级干果从开始销售至销售的第天的总销量(千克)与的关系为;乙级干果从开始销售至销售的第天的总销量(千克)与的关系为,且乙级干果的前三天的销售量的情况见下表:
1 2 3
21 44 69
(1)求、的值;
(2)若甲级干果与乙级干果分别以8元千克和6元千克的零售价出售,则卖完这批干果获得的毛利润是多少元?
(3)问从第几天起乙级干果每天的销量比甲级干果每天的销量至少多6千克?
(说明:毛利润销售总金额进货总金额.这批干果进货至卖完的过程中的损耗忽略不计)
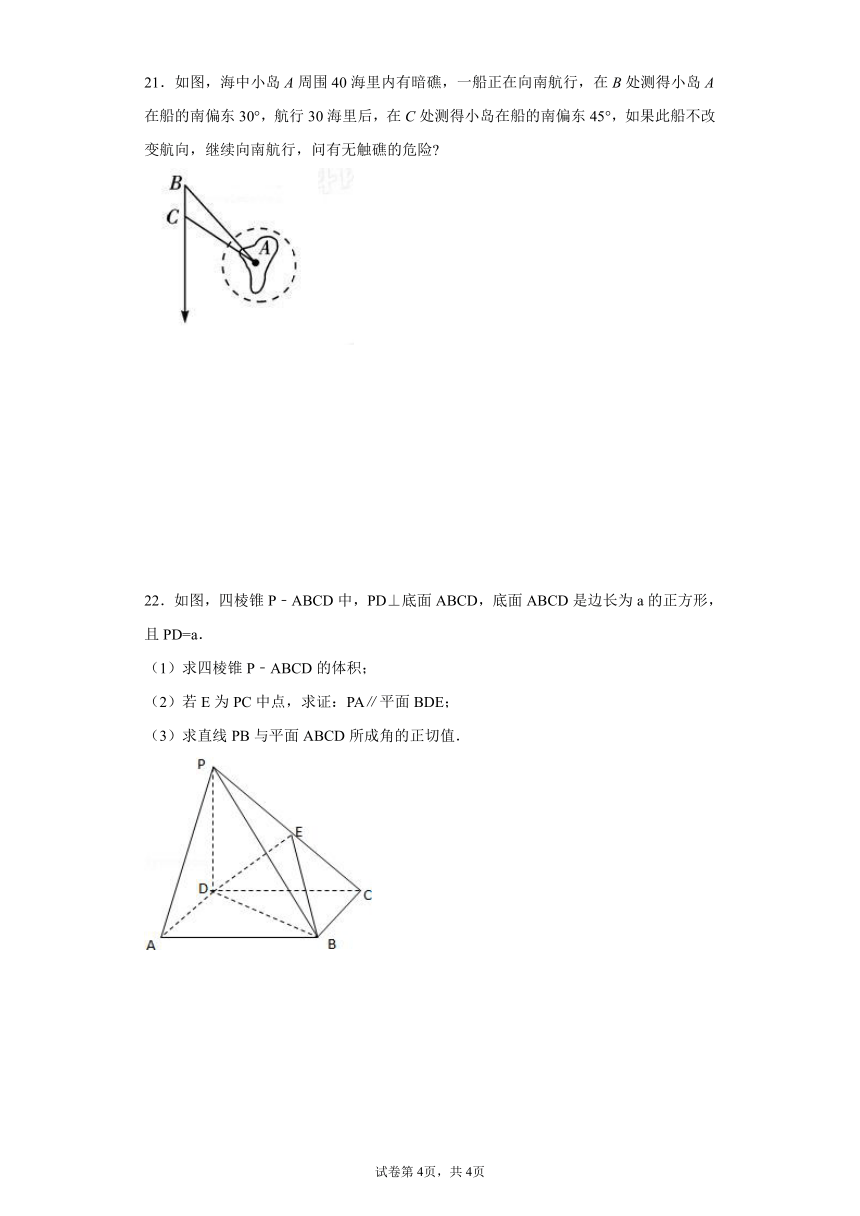
21.如图,海中小岛A周围40海里内有暗礁,一船正在向南航行,在B处测得小岛A在船的南偏东30°,航行30海里后,在C处测得小岛在船的南偏东45°,如果此船不改变航向,继续向南航行,问有无触礁的危险
22.如图,四棱锥P﹣ABCD中,PD⊥底面ABCD,底面ABCD是边长为a的正方形,且PD=a.
(1)求四棱锥P﹣ABCD的体积;
(2)若E为PC中点,求证:PA∥平面BDE;
(3)求直线PB与平面ABCD所成角的正切值.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.D
【详解】
因为全集,集合
,
,故选D.
2.B
【详解】
试题分析:由题意得,,故选B.
考点:指数幂运算及对数的运算性质.
3.D
【详解】
,,,
根据在上是增函数,所以,即.
故选:D.
4.C
【分析】
根据对数的运算法则逐一判断可得选项.
【详解】
对于A:,故A不正确;
对于B:,故B不正确;
对于C:∵,∴,故C正确,
对于D:,故D不正确,
故选: C.
5.C
【分析】
设菜园靠墙一边的长为米,则矩形菜园的宽为米,且,根据矩形的面积公式得到矩形的面积,再根据基本不等式求出最大值即可得解.
【详解】
设菜园靠墙一边的长为米,则矩形菜园的宽为米,且,
则菜园面积.当且仅当即时等号成立,
故选:C.
【点睛】
本题考查了函数的应用,考查了利用基本不等式求最值,属于基础题.
6.B
【分析】
先判断函数的单调性,然后利用零点存在性定理求解即可
【详解】
解:因为函数在上均为减函数,
所以函数在上为减函数,
因为,
所以函数的零点所在的区间为,
故选:B
【点睛】
此题考查零点存在性定理的应用,属于基础题
7.D
【解析】
【分析】
设出球的半径,由表面积求得半径,再由体积公式求解.
【详解】
解:设球的半径为R,则,可得.
该球的体积为.
故选:D.
【点睛】
本题考查球的表面积与体积公式,是基础的计算题.
8.C
【分析】
由平面的基本性质及其推论得:对于选项C,可能l∥n或l与n相交或l与n异面,即选项C错误,得解.
【详解】
由平行公理4可得选项A正确,由线面垂直的性质可得选项B正确,
由异面直线所成角的定义可得选项D正确,
对于选项C,若l∥α,n∥α,则l∥n或l与n相交或l与n异面,
即选项C错误,
故选C.
【点睛】
本题考查了平面中线线、线面的关系及性质定理与推论的应用,属简单题.
9.B
【分析】
根据直线垂直公式得到答案.
【详解】
已知直线,与互相垂直
或
故答案选B
【点睛】
本题考查了直线垂直的关系,意在考查学生的计算能力.
10.D
【分析】
由点与圆的位置关系可得出关于实数的不等式,由此可求得实数的取值范围.
【详解】
因为点在圆的内部,则,
解得.
故选:D.
11.C
【分析】
计算抽样间隔为,得到答案.
【详解】
学生40人,现用系统抽样的方法,从中抽取一个容量为4的样本,则抽样间隔为.
故.
故选:.
【点睛】
本题考查了系统抽样,意在考查学生对于系统抽样的理解和掌握.
12.B
【详解】
设夹谷石,则,
所以,
所以这批米内夹谷约为石,故选B.
考点:用样本的数据特征估计总体.
13.D
【分析】
表示投篮两次的所有基本事件情况,观察可得答案.
【详解】
某人连续投篮两次,共会发生:第一次中第二次不中,第一次不中第二次中,第一次中第二次中,第一次不中第二次不中,共4种情况
事件“至少投中一次”包含:第一次中第二次不中,第一次不中第二次中,第一次中第二次中,
所以与之互斥的就是“两次都不中”
故选:D
【点睛】
本题考查事件间的互斥关系,属于基础题.
14.C
【分析】
根据函数的图象变换规律,可得结论.
【详解】
将函数的图象上所有点的横坐标缩短到原来的(纵坐标不变),
所得图象对应的表达式为,
故选:C.
【点睛】
本题主要考查函数的图象变换规律,属于基础题.
15.D
【分析】
根据,且∥,由平面向量共线的坐标表示结合商数关系求解.
【详解】
因为,且∥,
所以,
即,
所以.
故选:D
【点睛】
本题主要考查平面向量共线的坐标表示以及同角三角函数基本关系式,还考查了运算求解的能力,属于中档题.
16.
【分析】
设的等比中项为,利用可得结果.
【详解】
因为
设的等比中项为,
所以,
可得,故答案为.
【点睛】
本题主要考查等比中项的性质与应用,意在考查求基础知识的掌握情况,属于简单题.
17.
【分析】
由一元二次不等式的解集可得求a、b,即可确定目标式的结果.
【详解】
由题设,,可得,
∴.
故答案为:
18.②④
【分析】
根据不等式性质判断前三个命题正确与否,第四个利用基本不等式求最值.
【详解】
当时,,①错,②对
当时,,③错
当时,,当且仅当时取等号,④对
【点睛】
本题考查不等式性质以及利用基本不等式求最值,考查基本分析判断与求解能力,属基础题.
19.①②
【分析】
利用奇偶性的定义判断①是否正确;利用函数图象的平移变换判断②是否正确;再分析函数的单调性判断③是否正确.
【详解】
对于①,当时,,则,所以为奇函数,故①正确;
对于②,由①可知函数为奇函数,图象关于原点对称,而看作是由的图象向上或向下平移个单位而得到,故图象关于对称,②正确;
对于③,当时,因为函数在上递减,所以,最大值为,故③错.
故答案为:①②.
20.(1)、的值分别是1、20;(2)798元;(3)第7天起.
【分析】
(1)根据表中的数据代入后,得到关于,的二元一次方程组,从而可求出解.
(2)设干果用天卖完,根据两个关系式和干果共有1140千克可列方程求解.然后用售价进价,得到利润.
(3)设第天乙级干果每天的销量比甲级干果每天的销量至少多6千克,从而可列出不等式求解.
【详解】
(1)根据表中的数据可得
.
答:、的值分别是1、20;
(2)甲级干果和乙级干果天售完这批货.
,解得,
当时,,,
毛利润(元,
答:卖完这批干果获得的毛利润是798元.
(3)设从第天起乙级干果每天的销量比甲级干果每天的销量至少多6千克,则甲、乙级干果的销售量为天的销售量减去天的销售量,
即甲级水果第天所卖出的干果数量:.
乙级水果第天所卖出的干果数量:,
,
解得:,
答:第7天起乙级干果每天的销量比甲级干果每天的销量至少多6千克.
【点睛】
本题考查理解题意的能力,关键是根据表格代入数列出二元一次方程组求出和,确定函数式,然后根据等量关系和不等量关系分别列方程和不等式求解.
21.无触礁的危险
【分析】
在中,由正弦定理可得,再利用直角三角形的性质可得A到BC所在直线的距离,与40比较大小,从而可得结果.
【详解】
在中, ,
∴,
由正弦定理知:,
∴,
∴A到BC所在直线的距离为
∴不改变航向,继续向南航行,无触礁的危险.
【点睛】
本题考查解三角形问题在生产实际中的运用,综合性强,是高考的重点,易错点是知识体系不牢固.解题时要认真审题,注意正弦定理和数形结合思想在解题中的合理运用.
22.见解析
【详解】
解:(1)四棱锥P﹣ABCD中,PD⊥底面ABCD,底面ABCD是边长为a的正方形,且PD=a.
所以:
=
证明:(2)在正方形ABCD中,连接AC和BD交与点O,连接OE,
所以:O是AC的中点,
由于E是PC的中点,
所以:OE是△PAC的中位线,
则:OE∥PA
OE 平面BDE
PA 平面BDE,
所以:PA∥平面BDE.
解:(3)PD⊥底面ABCD,底面ABCD是边长为a的正方形,且PD=a.
则:BD=
所以:∠PBD就是PB与平面ABCD所成角.
则:
所以:直线PB与平面ABCD所成角的正切值为
【点评】本题考查的知识要点:锥体的体积公式的应用,线面平行的判定,线面夹角的应用,属于基础题型.答案第1页,共2页
答案第1页,共2页
班级:___________姓名:___________座号:___________成绩:___________
一、单选题
1.若全集,集合,则( )
A. B. C. D.
2.已知是定义在上的奇函数,且当时,,则的值为
A. B. C. D.
3.设,,,则( )
A. B.
C. D.
4.下列等式成立的是( )
A. B.
C. D.
5.用一段长为36米的篱笆围成一个一边靠墙的矩形菜园.已知墙长20米,则菜园面积的最大值是( )
A.144 B.160 C.162 D.180
6.函数的零点所在的区间为( )
A. B.
C. D.
7.已知球的表面积为,则该球的体积为
A. B. C. D.
8.对于不同的直线l、、及平面,下列命题中错误的是
A.若,,则 B.若,,则
C.若,,则 D.若,,则
9.已知直线,与互相垂直,则的值是
A. B.或 C. D.或
10.已知点在圆的内部,则( )
A. B.
C. D.
11.某班有学生40人,现用系统抽样的方法,从中抽取一个容量为4的样本,已知样本中学生的座位号分别为4,,24,34,那么的值应是( )
A.12 B.13 C.14 D.15
12.我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为( )
A.134石 B.169石 C.338石 D.1365石
13.某人连续投篮两次,事件“至少投中一次”的互斥事件是( )
A.恰有一次投中 B.至多投中一次 C.两次都中 D.两次都不中
14.将函数的图象上所有点的横坐标缩短到原来的(纵坐标不变),所得图象对应的表达式为( )
A. B.
C. D.
15.已知向量,若∥,则的值等于( )
A. B. C.1 D.
二、填空题
16.,则的等比中项为_________.
17.不等式的解集是,则______.
18.给出下列四个命题:
①若a>b>0,则; ②若a>b>0,则; ③若a>b>0,则;
④若a>0,b>0,且a+b=1,则的最小值为4
其中正确命题的序号是____.(把你认为正确命题的序号都填上)
19.对于函数(),给出下列判断:
①当时,函数为奇函数;
②函数的图象关于点对称;
③当,时,函数的最小值为1.
其中正确的判断是_______.
三、解答题
20.某商店以6元千克的价格购进某种干果1140千克,并对其进行筛选分成甲级干果与乙级干果后同时开始销售.这批干果销售结束后,店主从销售统计中发现:甲级干果与乙级干果在销售过程中每天都有销量,且在同一天卖完;甲级干果从开始销售至销售的第天的总销量(千克)与的关系为;乙级干果从开始销售至销售的第天的总销量(千克)与的关系为,且乙级干果的前三天的销售量的情况见下表:
1 2 3
21 44 69
(1)求、的值;
(2)若甲级干果与乙级干果分别以8元千克和6元千克的零售价出售,则卖完这批干果获得的毛利润是多少元?
(3)问从第几天起乙级干果每天的销量比甲级干果每天的销量至少多6千克?
(说明:毛利润销售总金额进货总金额.这批干果进货至卖完的过程中的损耗忽略不计)
21.如图,海中小岛A周围40海里内有暗礁,一船正在向南航行,在B处测得小岛A在船的南偏东30°,航行30海里后,在C处测得小岛在船的南偏东45°,如果此船不改变航向,继续向南航行,问有无触礁的危险
22.如图,四棱锥P﹣ABCD中,PD⊥底面ABCD,底面ABCD是边长为a的正方形,且PD=a.
(1)求四棱锥P﹣ABCD的体积;
(2)若E为PC中点,求证:PA∥平面BDE;
(3)求直线PB与平面ABCD所成角的正切值.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.D
【详解】
因为全集,集合
,
,故选D.
2.B
【详解】
试题分析:由题意得,,故选B.
考点:指数幂运算及对数的运算性质.
3.D
【详解】
,,,
根据在上是增函数,所以,即.
故选:D.
4.C
【分析】
根据对数的运算法则逐一判断可得选项.
【详解】
对于A:,故A不正确;
对于B:,故B不正确;
对于C:∵,∴,故C正确,
对于D:,故D不正确,
故选: C.
5.C
【分析】
设菜园靠墙一边的长为米,则矩形菜园的宽为米,且,根据矩形的面积公式得到矩形的面积,再根据基本不等式求出最大值即可得解.
【详解】
设菜园靠墙一边的长为米,则矩形菜园的宽为米,且,
则菜园面积.当且仅当即时等号成立,
故选:C.
【点睛】
本题考查了函数的应用,考查了利用基本不等式求最值,属于基础题.
6.B
【分析】
先判断函数的单调性,然后利用零点存在性定理求解即可
【详解】
解:因为函数在上均为减函数,
所以函数在上为减函数,
因为,
所以函数的零点所在的区间为,
故选:B
【点睛】
此题考查零点存在性定理的应用,属于基础题
7.D
【解析】
【分析】
设出球的半径,由表面积求得半径,再由体积公式求解.
【详解】
解:设球的半径为R,则,可得.
该球的体积为.
故选:D.
【点睛】
本题考查球的表面积与体积公式,是基础的计算题.
8.C
【分析】
由平面的基本性质及其推论得:对于选项C,可能l∥n或l与n相交或l与n异面,即选项C错误,得解.
【详解】
由平行公理4可得选项A正确,由线面垂直的性质可得选项B正确,
由异面直线所成角的定义可得选项D正确,
对于选项C,若l∥α,n∥α,则l∥n或l与n相交或l与n异面,
即选项C错误,
故选C.
【点睛】
本题考查了平面中线线、线面的关系及性质定理与推论的应用,属简单题.
9.B
【分析】
根据直线垂直公式得到答案.
【详解】
已知直线,与互相垂直
或
故答案选B
【点睛】
本题考查了直线垂直的关系,意在考查学生的计算能力.
10.D
【分析】
由点与圆的位置关系可得出关于实数的不等式,由此可求得实数的取值范围.
【详解】
因为点在圆的内部,则,
解得.
故选:D.
11.C
【分析】
计算抽样间隔为,得到答案.
【详解】
学生40人,现用系统抽样的方法,从中抽取一个容量为4的样本,则抽样间隔为.
故.
故选:.
【点睛】
本题考查了系统抽样,意在考查学生对于系统抽样的理解和掌握.
12.B
【详解】
设夹谷石,则,
所以,
所以这批米内夹谷约为石,故选B.
考点:用样本的数据特征估计总体.
13.D
【分析】
表示投篮两次的所有基本事件情况,观察可得答案.
【详解】
某人连续投篮两次,共会发生:第一次中第二次不中,第一次不中第二次中,第一次中第二次中,第一次不中第二次不中,共4种情况
事件“至少投中一次”包含:第一次中第二次不中,第一次不中第二次中,第一次中第二次中,
所以与之互斥的就是“两次都不中”
故选:D
【点睛】
本题考查事件间的互斥关系,属于基础题.
14.C
【分析】
根据函数的图象变换规律,可得结论.
【详解】
将函数的图象上所有点的横坐标缩短到原来的(纵坐标不变),
所得图象对应的表达式为,
故选:C.
【点睛】
本题主要考查函数的图象变换规律,属于基础题.
15.D
【分析】
根据,且∥,由平面向量共线的坐标表示结合商数关系求解.
【详解】
因为,且∥,
所以,
即,
所以.
故选:D
【点睛】
本题主要考查平面向量共线的坐标表示以及同角三角函数基本关系式,还考查了运算求解的能力,属于中档题.
16.
【分析】
设的等比中项为,利用可得结果.
【详解】
因为
设的等比中项为,
所以,
可得,故答案为.
【点睛】
本题主要考查等比中项的性质与应用,意在考查求基础知识的掌握情况,属于简单题.
17.
【分析】
由一元二次不等式的解集可得求a、b,即可确定目标式的结果.
【详解】
由题设,,可得,
∴.
故答案为:
18.②④
【分析】
根据不等式性质判断前三个命题正确与否,第四个利用基本不等式求最值.
【详解】
当时,,①错,②对
当时,,③错
当时,,当且仅当时取等号,④对
【点睛】
本题考查不等式性质以及利用基本不等式求最值,考查基本分析判断与求解能力,属基础题.
19.①②
【分析】
利用奇偶性的定义判断①是否正确;利用函数图象的平移变换判断②是否正确;再分析函数的单调性判断③是否正确.
【详解】
对于①,当时,,则,所以为奇函数,故①正确;
对于②,由①可知函数为奇函数,图象关于原点对称,而看作是由的图象向上或向下平移个单位而得到,故图象关于对称,②正确;
对于③,当时,因为函数在上递减,所以,最大值为,故③错.
故答案为:①②.
20.(1)、的值分别是1、20;(2)798元;(3)第7天起.
【分析】
(1)根据表中的数据代入后,得到关于,的二元一次方程组,从而可求出解.
(2)设干果用天卖完,根据两个关系式和干果共有1140千克可列方程求解.然后用售价进价,得到利润.
(3)设第天乙级干果每天的销量比甲级干果每天的销量至少多6千克,从而可列出不等式求解.
【详解】
(1)根据表中的数据可得
.
答:、的值分别是1、20;
(2)甲级干果和乙级干果天售完这批货.
,解得,
当时,,,
毛利润(元,
答:卖完这批干果获得的毛利润是798元.
(3)设从第天起乙级干果每天的销量比甲级干果每天的销量至少多6千克,则甲、乙级干果的销售量为天的销售量减去天的销售量,
即甲级水果第天所卖出的干果数量:.
乙级水果第天所卖出的干果数量:,
,
解得:,
答:第7天起乙级干果每天的销量比甲级干果每天的销量至少多6千克.
【点睛】
本题考查理解题意的能力,关键是根据表格代入数列出二元一次方程组求出和,确定函数式,然后根据等量关系和不等量关系分别列方程和不等式求解.
21.无触礁的危险
【分析】
在中,由正弦定理可得,再利用直角三角形的性质可得A到BC所在直线的距离,与40比较大小,从而可得结果.
【详解】
在中, ,
∴,
由正弦定理知:,
∴,
∴A到BC所在直线的距离为
∴不改变航向,继续向南航行,无触礁的危险.
【点睛】
本题考查解三角形问题在生产实际中的运用,综合性强,是高考的重点,易错点是知识体系不牢固.解题时要认真审题,注意正弦定理和数形结合思想在解题中的合理运用.
22.见解析
【详解】
解:(1)四棱锥P﹣ABCD中,PD⊥底面ABCD,底面ABCD是边长为a的正方形,且PD=a.
所以:
=
证明:(2)在正方形ABCD中,连接AC和BD交与点O,连接OE,
所以:O是AC的中点,
由于E是PC的中点,
所以:OE是△PAC的中位线,
则:OE∥PA
OE 平面BDE
PA 平面BDE,
所以:PA∥平面BDE.
解:(3)PD⊥底面ABCD,底面ABCD是边长为a的正方形,且PD=a.
则:BD=
所以:∠PBD就是PB与平面ABCD所成角.
则:
所以:直线PB与平面ABCD所成角的正切值为
【点评】本题考查的知识要点:锥体的体积公式的应用,线面平行的判定,线面夹角的应用,属于基础题型.答案第1页,共2页
答案第1页,共2页
同课章节目录
