2021--2022学年人教版九年级数学下册27.2.1三边成比例的三角形相似课件(共18张PPT)
文档属性
| 名称 | 2021--2022学年人教版九年级数学下册27.2.1三边成比例的三角形相似课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 548.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-25 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
27.2.1 相似三角形的判定
第2课时 三边成比例的两个三角形相似
1. 复习已经学过的三角形相似的判定定理.
2. 掌握利用三边来判定两个三角形相似的方法,并能进
行相关计算. (重点、难点)
学习目标
复习引入
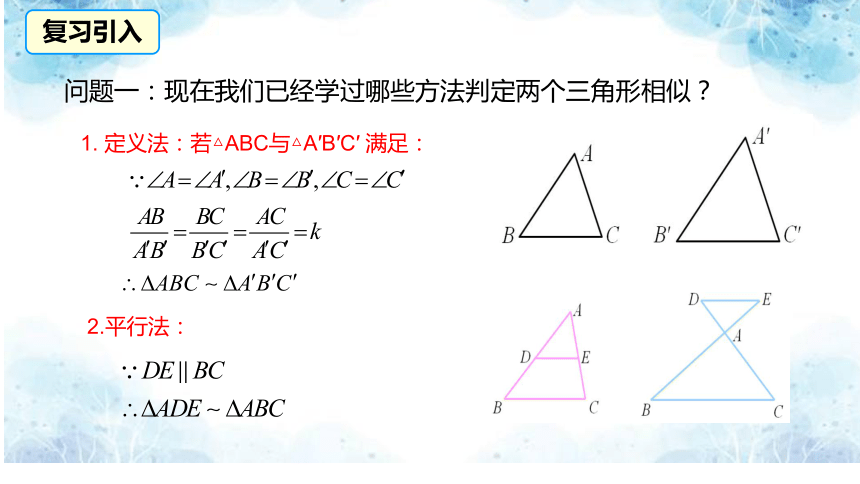
问题一:现在我们已经学过哪些方法判定两个三角形相似?
1. 定义法:若△ABC与△A′B′C′ 满足:
2.平行法:
合作探究
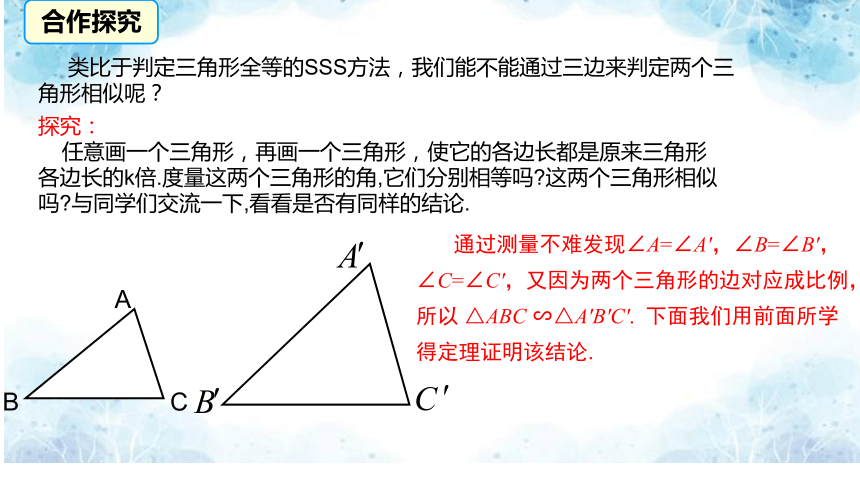
类比于判定三角形全等的SSS方法,我们能不能通过三边来判定两个三角形相似呢?
探究:
任意画一个三角形,再画一个三角形,使它的各边长都是原来三角形
各边长的k倍.度量这两个三角形的角,它们分别相等吗 这两个三角形相似
吗 与同学们交流一下,看看是否有同样的结论.
A
B
C
通过测量不难发现∠A=∠A',∠B=∠B',∠C=∠C',又因为两个三角形的边对应成比例,所以 △ABC ∽△A′B′C′. 下面我们用前面所学得定理证明该结论.
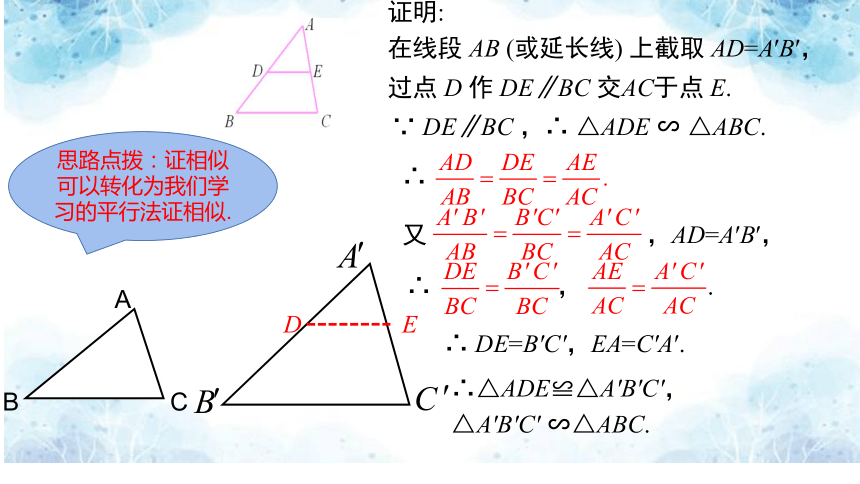
思路点拨:证相似可以转化为我们学行法证相似.
证明:
在线段 AB (或延长线) 上截取 AD=A′B′,
过点 D 作 DE∥BC 交AC于点 E.
A
B
C
D
E
∵ DE∥BC ,∴ △ADE ∽ △ABC.
∴
又 ,AD=A′B′,
∴ , .
∴ DE=B′C′,EA=C′A′.
∴△ADE≌△A′B′C′,
△A′B′C′ ∽△ABC.
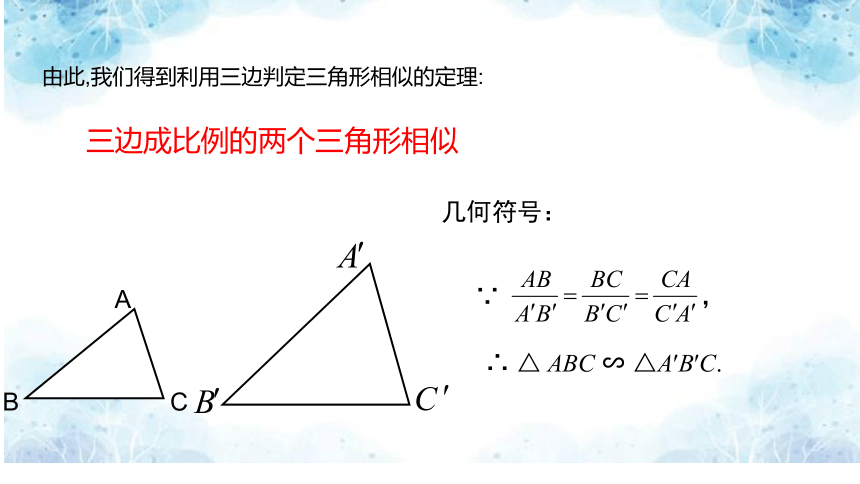
由此,我们得到利用三边判定三角形相似的定理:
A
B
C
三边成比例的两个三角形相似
∵ ,
∴ △ ABC ∽ △A′B′C.
几何符号:
例题讲解
例1.根据下列条件,判断
∴ △ ABC ∽ △A′B′C.
利用三边判断两个三角形相似的三个步骤:
(1)先三边大小顺序排列;
(2)分别计算边长的比值:
(3)通过比值是否相等判断相似.
变式训练1:
如图,网格图中每个方格都是边长为1的正方形,若A,B,C,D,E,F都是格点.求证:△ ABC ∽ △DEF.
思考:如何在网格中求格点三角形的边长
变式训练2:
如图,A(1,0),B(3,0),C(0,3),D(2,-1),P(2,2).
(1)
(2)在图中标出点D关于y轴的对称点D,连接AD,CD,判断ACD
的形状,并说明理由.
(3)求 的度数
思考: 可以转化为哪个角
当堂练习
1.图中的两个三角形是否相似 为什么
2.如图所示,已知
3. 如图,△ABC中,点 D,E,F 分别是 AB,BC,CA的中点,求证:△ABC∽△EFD.
∴ △ABC∽△EFD.
证明:∵△ABC中,点D,E,F分别是AB,BC,
CA的中点,
∴
∴
4. 如图,∠APD=90°,AP=PB=BC=CD,下列结论正确的是 ( )
A. △PAB∽△PCA B. △PAB∽△PDA
C. △ABC∽△DBA D. △ABC∽△DCA
A
C
B
P
D
C
∵ AB : BC = BD : AB = AD : AC,∴△ABC∽△DBA,故选C.
解析:设AP=PB=BC=CD=1,∵∠APD=90°,∴AB= ,AC= ,AD= .
拓展提升
5.如图,四边形ABCD、四边形CDEF和四边形EFGH是边长相等的正方形.
(1)
(2)求
1
2
6. 如图,某地四个乡镇 A,B,C,D 之间建有公路,
已知 AB = 14 千米,AD = 28 千米,BD = 21 千米,
DC = 31.5 千米,公路 AB 与 CD 平行吗?说出你
的理由.
A
C
B
D
28
14
21
42
31.5
解:公路 AB 与 CD 平行.
∴
∴ △ABD∽△BDC,
∴∠ABD=∠BDC,
∴AB∥DC.
课堂小结
本节课你的收获
1.相似的判定方法:
三边成比例的两个三角形相似
2.数学思想和方法:
转化思想和作辅助线的方法.
作业布置
教材第42页第1,2,3题
再见
27.2.1 相似三角形的判定
第2课时 三边成比例的两个三角形相似
1. 复习已经学过的三角形相似的判定定理.
2. 掌握利用三边来判定两个三角形相似的方法,并能进
行相关计算. (重点、难点)
学习目标
复习引入
问题一:现在我们已经学过哪些方法判定两个三角形相似?
1. 定义法:若△ABC与△A′B′C′ 满足:
2.平行法:
合作探究
类比于判定三角形全等的SSS方法,我们能不能通过三边来判定两个三角形相似呢?
探究:
任意画一个三角形,再画一个三角形,使它的各边长都是原来三角形
各边长的k倍.度量这两个三角形的角,它们分别相等吗 这两个三角形相似
吗 与同学们交流一下,看看是否有同样的结论.
A
B
C
通过测量不难发现∠A=∠A',∠B=∠B',∠C=∠C',又因为两个三角形的边对应成比例,所以 △ABC ∽△A′B′C′. 下面我们用前面所学得定理证明该结论.
思路点拨:证相似可以转化为我们学行法证相似.
证明:
在线段 AB (或延长线) 上截取 AD=A′B′,
过点 D 作 DE∥BC 交AC于点 E.
A
B
C
D
E
∵ DE∥BC ,∴ △ADE ∽ △ABC.
∴
又 ,AD=A′B′,
∴ , .
∴ DE=B′C′,EA=C′A′.
∴△ADE≌△A′B′C′,
△A′B′C′ ∽△ABC.
由此,我们得到利用三边判定三角形相似的定理:
A
B
C
三边成比例的两个三角形相似
∵ ,
∴ △ ABC ∽ △A′B′C.
几何符号:
例题讲解
例1.根据下列条件,判断
∴ △ ABC ∽ △A′B′C.
利用三边判断两个三角形相似的三个步骤:
(1)先三边大小顺序排列;
(2)分别计算边长的比值:
(3)通过比值是否相等判断相似.
变式训练1:
如图,网格图中每个方格都是边长为1的正方形,若A,B,C,D,E,F都是格点.求证:△ ABC ∽ △DEF.
思考:如何在网格中求格点三角形的边长
变式训练2:
如图,A(1,0),B(3,0),C(0,3),D(2,-1),P(2,2).
(1)
(2)在图中标出点D关于y轴的对称点D,连接AD,CD,判断ACD
的形状,并说明理由.
(3)求 的度数
思考: 可以转化为哪个角
当堂练习
1.图中的两个三角形是否相似 为什么
2.如图所示,已知
3. 如图,△ABC中,点 D,E,F 分别是 AB,BC,CA的中点,求证:△ABC∽△EFD.
∴ △ABC∽△EFD.
证明:∵△ABC中,点D,E,F分别是AB,BC,
CA的中点,
∴
∴
4. 如图,∠APD=90°,AP=PB=BC=CD,下列结论正确的是 ( )
A. △PAB∽△PCA B. △PAB∽△PDA
C. △ABC∽△DBA D. △ABC∽△DCA
A
C
B
P
D
C
∵ AB : BC = BD : AB = AD : AC,∴△ABC∽△DBA,故选C.
解析:设AP=PB=BC=CD=1,∵∠APD=90°,∴AB= ,AC= ,AD= .
拓展提升
5.如图,四边形ABCD、四边形CDEF和四边形EFGH是边长相等的正方形.
(1)
(2)求
1
2
6. 如图,某地四个乡镇 A,B,C,D 之间建有公路,
已知 AB = 14 千米,AD = 28 千米,BD = 21 千米,
DC = 31.5 千米,公路 AB 与 CD 平行吗?说出你
的理由.
A
C
B
D
28
14
21
42
31.5
解:公路 AB 与 CD 平行.
∴
∴ △ABD∽△BDC,
∴∠ABD=∠BDC,
∴AB∥DC.
课堂小结
本节课你的收获
1.相似的判定方法:
三边成比例的两个三角形相似
2.数学思想和方法:
转化思想和作辅助线的方法.
作业布置
教材第42页第1,2,3题
再见
