2021-2022学年人教版数学九年级上册24.4弧长及扇形面积 课件(共20张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学九年级上册24.4弧长及扇形面积 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 591.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-25 11:24:35 | ||
图片预览







文档简介
(共20张PPT)
24.4 弧长和扇形面积
1.弧长、扇形面积公式;
2.不规则图形的面积的求法:用规则的图形的面积来表示;
3.数学思想转化的应用:化归思想。
学习目标
o
圆的周长公式
圆的面积公式
C=2πr
S=πr2
知识回顾
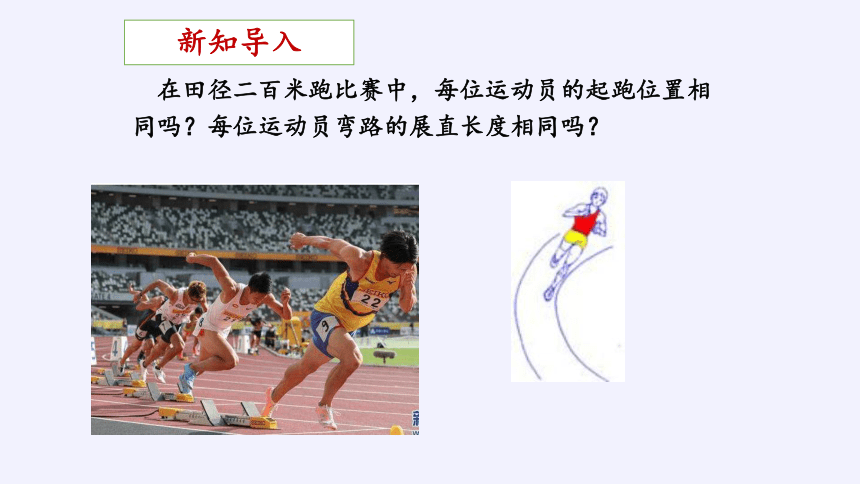
在田径二百米跑比赛中,每位运动员的起跑位置相同吗?每位运动员弯路的展直长度相同吗?
新知导入
探究新知
探究1:
问题1:如果圆形跑道的半径是30米,圆心角是180°,那么半圆形跑道长是多少呢?
问题2:如果将1中的圆心角变成是90°、30°,那么所对应的弧长分别是多少呢?
问题3:已知⊙O半径为R,求n°圆心角所对弧长.
结论1:
弧长公式:
练习一:
(1)已知圆弧的半径为24,所对的圆心角为60°,它的弧长为__________.
(2)已知一弧长为12πcm,此弧所对的圆心角为240°,则此弧所在圆的半径为_________.
探究二:
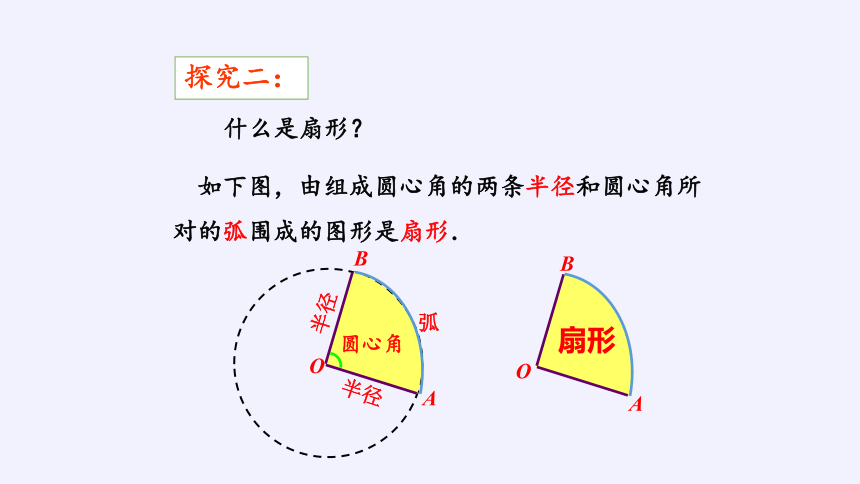
什么是扇形?
如下图,由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形.
半径
半径
O
B
A
圆心角
弧
O
B
A
扇形
扇形的面积就是圆面积的一部分.想一想1°的圆心角所对的扇形面积是多少?n°的圆心角呢?
结 论2 :
S扇形= S圆
360
n
360
n
= πr2
扇形的面积公式与弧长公式有联系吗?
类似于哪个公式呢?
l
比较这两个公式,
你能用l和R来表示S扇吗?
(2)扇形的圆心角为60°,半径为5cm,则这个扇形的弧长为_______, 这个扇形的面积为______.
(1)一个扇形的弧长为20πcm,半径为24cm,则该扇形的面积为_______.
练习二:
1、如图所示,把边长为2的正方形ABCD的一边放在定
直线L上,按顺时针方向绕点D旋转到如图的位置,
则点B运动到点B′所经过的路线长度为______ ;
A
C
B
D
B/
C/
(A/)
L
小试牛刀
2、如图:在△AOC中,∠AOC=900,
∠C=150,以O为圆心,AO为半径的
圆交AC与B点,若OA=6,求弧AB的长。
A
C
B
O
例:如图、水平放置的圆柱形排水管道的截面
半径是0.6m,其中水面高0.3m,求截面
上有水部分的面积。
0
B
A
C
D
例题讲解
弓形的面积 = S扇-S△
变式:如图、水平放置的圆柱形排水管道
的截面半径是0.6cm,其中水面高
0.9cm,求截面上有水部分的面积。
0
A
B
D
C
E
弓形的面积 = S扇+ S△
变式:如图,A是半径为1的圆O外一点,且OA=2,
AB是⊙O的切线,BC//OA,连结AC,则阴
影部分面积等于 。
例1 如图,△ABC是⊙O的内接三角形,∠BAC=60°.设⊙O的半径为2,求 的长.
拓展练习:
分析:∠BOC=120°
例2:如图,折扇完全打开后,OA、OB的夹角为120°,OA的长为30cm,AC的长为20cm,求图中阴影部分的面积S.
S阴影 = S扇形OAB - S扇形OCD
例3:如图,半圆的直径AB=40,C、D是半圆的3等分点.求弦AC、AD与 围成的阴影部分的面积.
1.弧长、扇形面积公式;
2.不规则图形的面积的求法:用规则的图形的面积来表示;
3.数学思想转化的应用:化归思想.
课堂小结
谢 谢
24.4 弧长和扇形面积
1.弧长、扇形面积公式;
2.不规则图形的面积的求法:用规则的图形的面积来表示;
3.数学思想转化的应用:化归思想。
学习目标
o
圆的周长公式
圆的面积公式
C=2πr
S=πr2
知识回顾
在田径二百米跑比赛中,每位运动员的起跑位置相同吗?每位运动员弯路的展直长度相同吗?
新知导入
探究新知
探究1:
问题1:如果圆形跑道的半径是30米,圆心角是180°,那么半圆形跑道长是多少呢?
问题2:如果将1中的圆心角变成是90°、30°,那么所对应的弧长分别是多少呢?
问题3:已知⊙O半径为R,求n°圆心角所对弧长.
结论1:
弧长公式:
练习一:
(1)已知圆弧的半径为24,所对的圆心角为60°,它的弧长为__________.
(2)已知一弧长为12πcm,此弧所对的圆心角为240°,则此弧所在圆的半径为_________.
探究二:
什么是扇形?
如下图,由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形.
半径
半径
O
B
A
圆心角
弧
O
B
A
扇形
扇形的面积就是圆面积的一部分.想一想1°的圆心角所对的扇形面积是多少?n°的圆心角呢?
结 论2 :
S扇形= S圆
360
n
360
n
= πr2
扇形的面积公式与弧长公式有联系吗?
类似于哪个公式呢?
l
比较这两个公式,
你能用l和R来表示S扇吗?
(2)扇形的圆心角为60°,半径为5cm,则这个扇形的弧长为_______, 这个扇形的面积为______.
(1)一个扇形的弧长为20πcm,半径为24cm,则该扇形的面积为_______.
练习二:
1、如图所示,把边长为2的正方形ABCD的一边放在定
直线L上,按顺时针方向绕点D旋转到如图的位置,
则点B运动到点B′所经过的路线长度为______ ;
A
C
B
D
B/
C/
(A/)
L
小试牛刀
2、如图:在△AOC中,∠AOC=900,
∠C=150,以O为圆心,AO为半径的
圆交AC与B点,若OA=6,求弧AB的长。
A
C
B
O
例:如图、水平放置的圆柱形排水管道的截面
半径是0.6m,其中水面高0.3m,求截面
上有水部分的面积。
0
B
A
C
D
例题讲解
弓形的面积 = S扇-S△
变式:如图、水平放置的圆柱形排水管道
的截面半径是0.6cm,其中水面高
0.9cm,求截面上有水部分的面积。
0
A
B
D
C
E
弓形的面积 = S扇+ S△
变式:如图,A是半径为1的圆O外一点,且OA=2,
AB是⊙O的切线,BC//OA,连结AC,则阴
影部分面积等于 。
例1 如图,△ABC是⊙O的内接三角形,∠BAC=60°.设⊙O的半径为2,求 的长.
拓展练习:
分析:∠BOC=120°
例2:如图,折扇完全打开后,OA、OB的夹角为120°,OA的长为30cm,AC的长为20cm,求图中阴影部分的面积S.
S阴影 = S扇形OAB - S扇形OCD
例3:如图,半圆的直径AB=40,C、D是半圆的3等分点.求弦AC、AD与 围成的阴影部分的面积.
1.弧长、扇形面积公式;
2.不规则图形的面积的求法:用规则的图形的面积来表示;
3.数学思想转化的应用:化归思想.
课堂小结
谢 谢
同课章节目录
