沪科版数学八年级上册 11.2 图形在坐标系中的平移课件(共26张PPT)
文档属性
| 名称 | 沪科版数学八年级上册 11.2 图形在坐标系中的平移课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 856.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-25 09:42:18 | ||
图片预览




文档简介
(共26张PPT)
11.2 图形在坐标系中的平移
1、能在直角坐标系中用坐标的方法研究图形的变换,掌握图形在平移过程中各点坐标的变化规律,理解图形在平面坐标系上的平移实质上就是点坐标的对应变换;
2、运用图形在直角坐标系中平移的点坐标的变化规律进行简单的平移作图;
3、经历观察、分析、抽象、归纳等过程,经历与他人合作交流的过程,进一步发展数形结合的思想与空间观念.
-3
-2
-1
O
1
2
3
x
y
1
3
2
-2
-1
-3
A
B
D
C
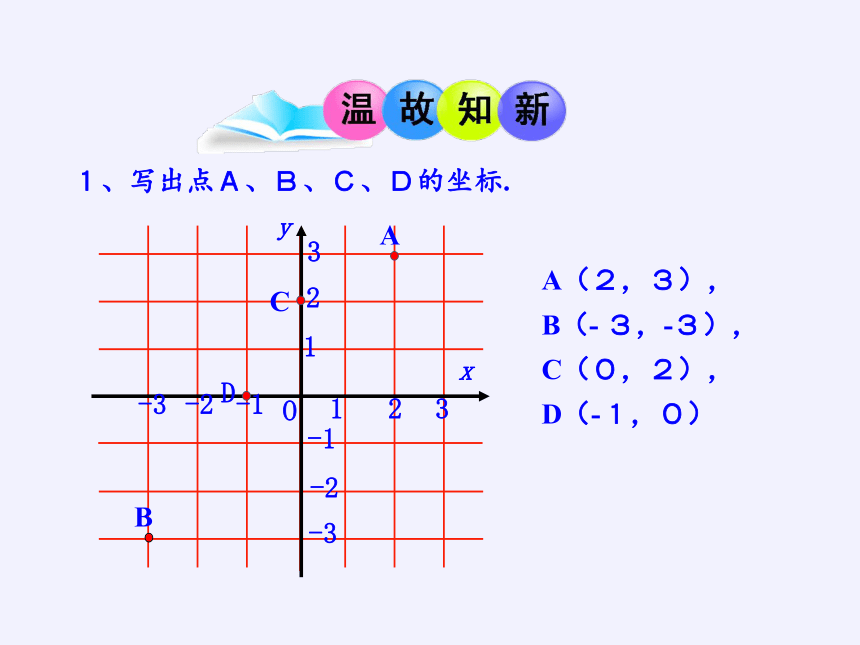
1、写出点A、B、C、D的坐标.
A(2,3),
B(- 3,-3),
C(0,2),
D(-1,0)
2.下列各点分别在坐标平面的什么位置上?
A(3,2)
B(0,-2)
C(-3,-2)
D(-3,0)
E(-1.5,3.5)
F(2,-3)
第一象限
第三象限
第二象限
第四象限
y轴上
x轴上
(+,+)
(-,+)
(-,-)
(+,-)
(0,y)
(x,0)
每个象限内的点都有自己的符号特征.
3、点到两轴的距离与坐标有什么关系?
4、对称点的坐标特征:
6、两轴角平分线坐标特征:
5、平行于两轴的直线上的点的坐标有什么特征?
A
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
O
E
3
4
2
-1
5
-2
-3
-4
-6
-5
6
1
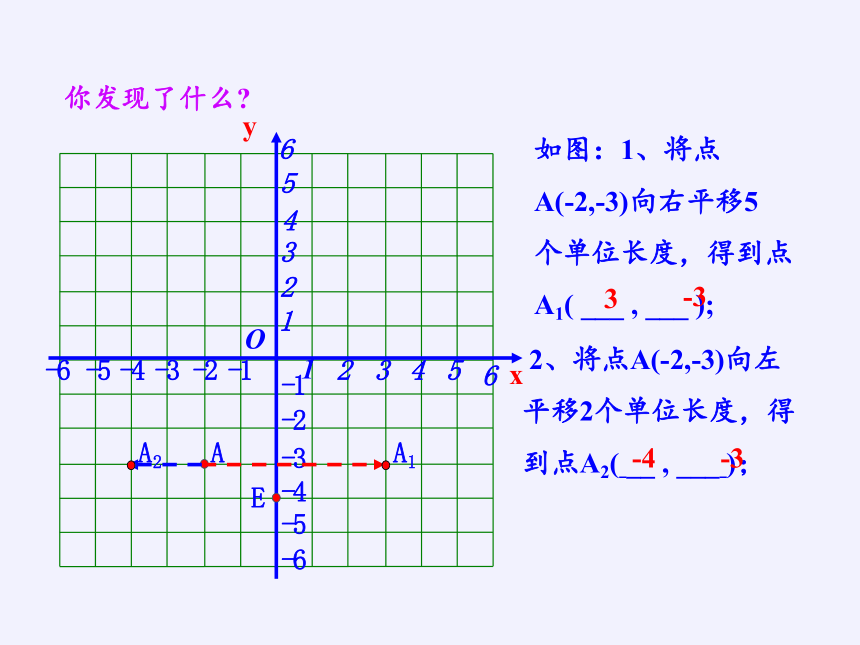
如图:1、将点
A(-2,-3)向右平移5
个单位长度,得到点A1( ___ , ___ );
2、将点A(-2,-3)向左
平移2个单位长度,得
到点A2( __ , ___ );
A1
-4
-3
3
-3
A2
你发现了什么
y
x
A
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
0
E
3
4
2
-1
5
-2
-3
-4
-6
-5
6
0
1
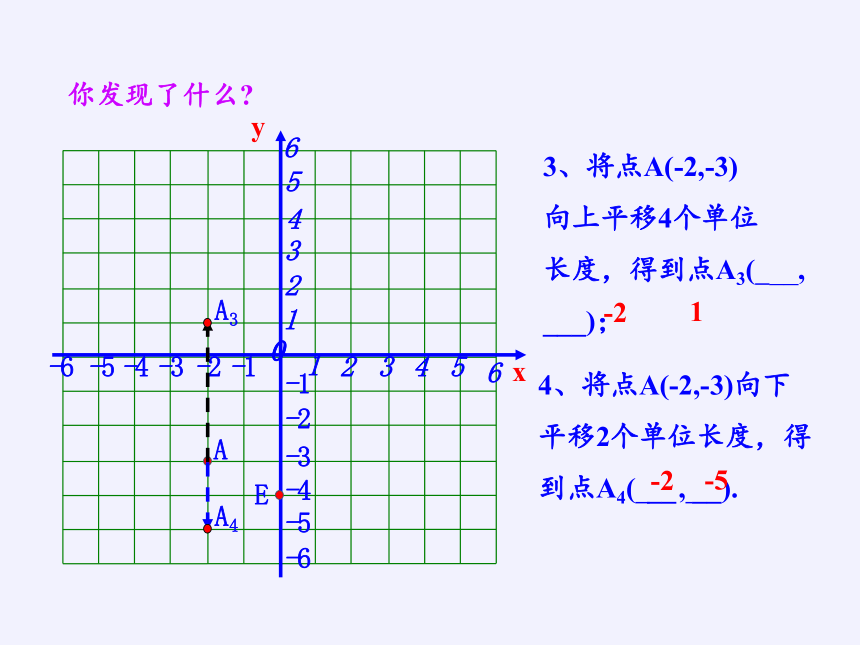
3、将点A(-2,-3)
向上平移4个单位
长度,得到点A3( __, ___);
4、将点A(-2,-3)向下平移2个单位长度,得到点A4( __, __).
A3
A4
-2
1
-2
-5
你发现了什么
y
x
2、将点(x,y)向上(或下)平移b个单位长度,可以得
到对应点(x ,y +b)或 ( , ).
1、将点(x,y)向右(或左)平移a个单位长度,可以得
到对应点(x+a,y)或( , ).
在平面直角坐标系中,
x - a
y
x
y -b
左、右平移纵坐标不变,横坐标变,变化规律是左减右加;
一个图形在平面直角坐标系中进行平移,其坐标就要
发生相应的变化, 可以简单地理解为:
上、下平移横坐标不变,纵坐标变,变化规律是上加下减.
【例1】如图,将△ABC向左平移2个单位长度再向下平移3个单位长度,则A、B、C各点的坐标变为多少
A
B
C
-4
-5
1
2
3
4
1
2
3
4
-1
-2
-3
-1
-2
-3
o
x
y
O
A1(-1,-1)
B1(-3,-4)
C1(1,-5)
(A1)
(B1)
(C1)
已知点A(-2,-3):
1、(1)将点A向右平移5个单位长度得到点A1,则点A1
的坐标是 ;
(2)将点A向右平移6个单位长度得到点A2,则点A2
的坐标是 ;
(3)将点A向右平移a(a>0)个单位长度得到点An,则点
An的坐标是 ;
(4)将点A向左平移a(a>0)个单位长度得到点Bn,则
点Bn的坐标是 ;
(-2-a ,-3)
(3,-3)
(4,-3)
(-2+ a ,-3)
o
0
-2
-3
-1
-2
-3
-1
2
3
1
1
2
3
【例2】如图,△ABC,三个顶点的坐标分别是A(4,3),B(3,1),C(1,2).
(1) 将△ABC三个顶点的横坐标都减去6,纵坐标不变,分别得到点A1,B1,C1,依次连接A1,B1,C1各点所得△A1B1C1与三角形ABC的大小、形状和位置有什么关系?
x
A
B
C
y
A
B
C
C1
A1
B1
【解析】如图所得△A1B1C1与△ABC的大小、形状完全相同, △A1B1C1可以看作是△ABC向左平移6个单位得到的.
o
0
-2
-3
-1
-2
-3
-1
2
3
1
1
2
3
(2)将△ABC三个顶点的
纵坐标都减去5,横坐标
不变,分别得到点A2,B2,
C2,依次连接A2、B2、C2
各点所得△A2B2C2与
△ABC的大小、形状和位置
有什么关系?
x
A
B
C
y
A
B
C
C2
A2
B2
【解析】如图所得
△A2B2C2与△ ABC的
大小、形状完全相同,
△ A2B2C2可以看作是△ABC向下平移5个
单位得到的.
请归纳:
通过观察坐标的变化得到图形的变化情况?
1.点A(4,-1)平移到点B(-1,4),可看作先向
平移 个单位,再向 平移
个单位;也可以看作先向 平移
个单位,再向 平移 个单
位.
2.点M向左平移4个单位后的坐标为(-1,2),则点M
开始时的坐标为 .
左
5
上
5
上
5
左
5
(3,2)
1、将四边形ABCD的四个顶点的横坐标都减去6,同时纵坐标都减去5,得到的结论是( ).
A.先向左平移6个单位,再向下平移5个单位.
B.先向右平移6各单位,再向下平移5各单位.
C.先向左平移6各单位,再向上平移5各单位.
D.先向右平移6个单位,再向上平移5各单位.
【解析】选A.横坐标减去6,向左平移6个单位,纵坐标减
去5,向下平移5个单位.
2、(宿迁·中考)在平面直角坐标系中,线段AB的端点A的坐标为(-3,2),将其先向右平移4个单位,再向下平移3个单位,得到线段A′B′,则点A对应点A′的坐标为_____.
【解析】根据平移的规律(x,y)向右平移4个单位,再向下平移3个单位,得(x+4,y-3),所以(-3,2)经平移后坐标为(1,-1)
答案:(1,-1)
1
2
3
4
1
0
4
3
2
–2
–1
–1
–2
–3
–3
1
2
3
4
1
0
4
3
2
–2
–1
–1
–2
–3
–3
思考
左图中点P(x0, y0)平移后得到的右图的点的左标是?
4
3.观察下列图形,与图(1)中的鱼相比,图(2)中的鱼发生了一些变化,若图(1)中鱼上P点的坐标为(4,3.2)则这个点在图(2)中的对应点P的坐标应为_____;
y
1
1
-1
-2
-3
2
3
4
5
3
2
O
1
1
-1
-2
-3
2
3
4
4
5
3
2
O
图1
图2
P
●
P
●
ⅹ
ⅹ
y
(4,2.2)
A
B
C
-4
-5
1
2
3
4
1
2
3
4
-1
-2
-3
-1
-2
-3
o
x
y
(-3,2)
(-2,-1)
(3,0)
4、如图,△ABC上任意一点P(x0,y0)经平移后得到的对应点为P1(x0+2,y0+4),将△ABC作同样的平移得到△A1B1C1.求A1、B1、C1的坐标.
P(x0,y0)
P1(x0+2,y0+4)
B
C
B1
A1
C1
【解析】A(-3,2)经平移后
得到(-3+2,2+4),即A1(-1,
6);B(-2,-1)经平移后得到
(-2+2,-1+4),即B1(0,3);
C(3,0)经平移后得到(3+2,0+4),即C1(5,4).
对一个图形进行平移,这个图形上所有点的坐标都要发生相应的变化;反过来,从图形上的点的坐标的某种变化,我们也可以看出对这个图形进行了怎样的平移.
【规律方法】
1、如果把一个图形各个点的横坐标都加(或减去)一
个正数a,相应的新图形就是把原图形向 (或向 )
平移 个单位长度;
2、如果把一个图形各个点的纵坐标都加(或减去)一个
正数a,相应的新图形就是把原图形向 (或
向 )平移 个单位长度.
在平面直角坐标系内:
右
左
a
a
上
下
通过本课时的学习,需要我们掌握:
平面坐标系内点的平移规律
在平面直角坐标系中,将点(x,y)向右(或左)平移a个单位长度,对应点的横坐标加上a(或减去a),而纵坐标不变,即坐标变为(x+a,y)或(x-a,y).
在平面直角坐标系中,将点(x,y)向上(或下)平移b个单位长度,对应点的纵坐标加上b(或减去b),而横坐标不变,即坐标变为(x,y+b)或(x,y-b).
信心来自于实力,实力来自于努力.
谢 谢
11.2 图形在坐标系中的平移
1、能在直角坐标系中用坐标的方法研究图形的变换,掌握图形在平移过程中各点坐标的变化规律,理解图形在平面坐标系上的平移实质上就是点坐标的对应变换;
2、运用图形在直角坐标系中平移的点坐标的变化规律进行简单的平移作图;
3、经历观察、分析、抽象、归纳等过程,经历与他人合作交流的过程,进一步发展数形结合的思想与空间观念.
-3
-2
-1
O
1
2
3
x
y
1
3
2
-2
-1
-3
A
B
D
C
1、写出点A、B、C、D的坐标.
A(2,3),
B(- 3,-3),
C(0,2),
D(-1,0)
2.下列各点分别在坐标平面的什么位置上?
A(3,2)
B(0,-2)
C(-3,-2)
D(-3,0)
E(-1.5,3.5)
F(2,-3)
第一象限
第三象限
第二象限
第四象限
y轴上
x轴上
(+,+)
(-,+)
(-,-)
(+,-)
(0,y)
(x,0)
每个象限内的点都有自己的符号特征.
3、点到两轴的距离与坐标有什么关系?
4、对称点的坐标特征:
6、两轴角平分线坐标特征:
5、平行于两轴的直线上的点的坐标有什么特征?
A
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
O
E
3
4
2
-1
5
-2
-3
-4
-6
-5
6
1
如图:1、将点
A(-2,-3)向右平移5
个单位长度,得到点A1( ___ , ___ );
2、将点A(-2,-3)向左
平移2个单位长度,得
到点A2( __ , ___ );
A1
-4
-3
3
-3
A2
你发现了什么
y
x
A
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
0
E
3
4
2
-1
5
-2
-3
-4
-6
-5
6
0
1
3、将点A(-2,-3)
向上平移4个单位
长度,得到点A3( __, ___);
4、将点A(-2,-3)向下平移2个单位长度,得到点A4( __, __).
A3
A4
-2
1
-2
-5
你发现了什么
y
x
2、将点(x,y)向上(或下)平移b个单位长度,可以得
到对应点(x ,y +b)或 ( , ).
1、将点(x,y)向右(或左)平移a个单位长度,可以得
到对应点(x+a,y)或( , ).
在平面直角坐标系中,
x - a
y
x
y -b
左、右平移纵坐标不变,横坐标变,变化规律是左减右加;
一个图形在平面直角坐标系中进行平移,其坐标就要
发生相应的变化, 可以简单地理解为:
上、下平移横坐标不变,纵坐标变,变化规律是上加下减.
【例1】如图,将△ABC向左平移2个单位长度再向下平移3个单位长度,则A、B、C各点的坐标变为多少
A
B
C
-4
-5
1
2
3
4
1
2
3
4
-1
-2
-3
-1
-2
-3
o
x
y
O
A1(-1,-1)
B1(-3,-4)
C1(1,-5)
(A1)
(B1)
(C1)
已知点A(-2,-3):
1、(1)将点A向右平移5个单位长度得到点A1,则点A1
的坐标是 ;
(2)将点A向右平移6个单位长度得到点A2,则点A2
的坐标是 ;
(3)将点A向右平移a(a>0)个单位长度得到点An,则点
An的坐标是 ;
(4)将点A向左平移a(a>0)个单位长度得到点Bn,则
点Bn的坐标是 ;
(-2-a ,-3)
(3,-3)
(4,-3)
(-2+ a ,-3)
o
0
-2
-3
-1
-2
-3
-1
2
3
1
1
2
3
【例2】如图,△ABC,三个顶点的坐标分别是A(4,3),B(3,1),C(1,2).
(1) 将△ABC三个顶点的横坐标都减去6,纵坐标不变,分别得到点A1,B1,C1,依次连接A1,B1,C1各点所得△A1B1C1与三角形ABC的大小、形状和位置有什么关系?
x
A
B
C
y
A
B
C
C1
A1
B1
【解析】如图所得△A1B1C1与△ABC的大小、形状完全相同, △A1B1C1可以看作是△ABC向左平移6个单位得到的.
o
0
-2
-3
-1
-2
-3
-1
2
3
1
1
2
3
(2)将△ABC三个顶点的
纵坐标都减去5,横坐标
不变,分别得到点A2,B2,
C2,依次连接A2、B2、C2
各点所得△A2B2C2与
△ABC的大小、形状和位置
有什么关系?
x
A
B
C
y
A
B
C
C2
A2
B2
【解析】如图所得
△A2B2C2与△ ABC的
大小、形状完全相同,
△ A2B2C2可以看作是△ABC向下平移5个
单位得到的.
请归纳:
通过观察坐标的变化得到图形的变化情况?
1.点A(4,-1)平移到点B(-1,4),可看作先向
平移 个单位,再向 平移
个单位;也可以看作先向 平移
个单位,再向 平移 个单
位.
2.点M向左平移4个单位后的坐标为(-1,2),则点M
开始时的坐标为 .
左
5
上
5
上
5
左
5
(3,2)
1、将四边形ABCD的四个顶点的横坐标都减去6,同时纵坐标都减去5,得到的结论是( ).
A.先向左平移6个单位,再向下平移5个单位.
B.先向右平移6各单位,再向下平移5各单位.
C.先向左平移6各单位,再向上平移5各单位.
D.先向右平移6个单位,再向上平移5各单位.
【解析】选A.横坐标减去6,向左平移6个单位,纵坐标减
去5,向下平移5个单位.
2、(宿迁·中考)在平面直角坐标系中,线段AB的端点A的坐标为(-3,2),将其先向右平移4个单位,再向下平移3个单位,得到线段A′B′,则点A对应点A′的坐标为_____.
【解析】根据平移的规律(x,y)向右平移4个单位,再向下平移3个单位,得(x+4,y-3),所以(-3,2)经平移后坐标为(1,-1)
答案:(1,-1)
1
2
3
4
1
0
4
3
2
–2
–1
–1
–2
–3
–3
1
2
3
4
1
0
4
3
2
–2
–1
–1
–2
–3
–3
思考
左图中点P(x0, y0)平移后得到的右图的点的左标是?
4
3.观察下列图形,与图(1)中的鱼相比,图(2)中的鱼发生了一些变化,若图(1)中鱼上P点的坐标为(4,3.2)则这个点在图(2)中的对应点P的坐标应为_____;
y
1
1
-1
-2
-3
2
3
4
5
3
2
O
1
1
-1
-2
-3
2
3
4
4
5
3
2
O
图1
图2
P
●
P
●
ⅹ
ⅹ
y
(4,2.2)
A
B
C
-4
-5
1
2
3
4
1
2
3
4
-1
-2
-3
-1
-2
-3
o
x
y
(-3,2)
(-2,-1)
(3,0)
4、如图,△ABC上任意一点P(x0,y0)经平移后得到的对应点为P1(x0+2,y0+4),将△ABC作同样的平移得到△A1B1C1.求A1、B1、C1的坐标.
P(x0,y0)
P1(x0+2,y0+4)
B
C
B1
A1
C1
【解析】A(-3,2)经平移后
得到(-3+2,2+4),即A1(-1,
6);B(-2,-1)经平移后得到
(-2+2,-1+4),即B1(0,3);
C(3,0)经平移后得到(3+2,0+4),即C1(5,4).
对一个图形进行平移,这个图形上所有点的坐标都要发生相应的变化;反过来,从图形上的点的坐标的某种变化,我们也可以看出对这个图形进行了怎样的平移.
【规律方法】
1、如果把一个图形各个点的横坐标都加(或减去)一
个正数a,相应的新图形就是把原图形向 (或向 )
平移 个单位长度;
2、如果把一个图形各个点的纵坐标都加(或减去)一个
正数a,相应的新图形就是把原图形向 (或
向 )平移 个单位长度.
在平面直角坐标系内:
右
左
a
a
上
下
通过本课时的学习,需要我们掌握:
平面坐标系内点的平移规律
在平面直角坐标系中,将点(x,y)向右(或左)平移a个单位长度,对应点的横坐标加上a(或减去a),而纵坐标不变,即坐标变为(x+a,y)或(x-a,y).
在平面直角坐标系中,将点(x,y)向上(或下)平移b个单位长度,对应点的纵坐标加上b(或减去b),而横坐标不变,即坐标变为(x,y+b)或(x,y-b).
信心来自于实力,实力来自于努力.
谢 谢
