沪科版数学八年级上册 13.1.1三角形边角关系课件(共15张PPT)
文档属性
| 名称 | 沪科版数学八年级上册 13.1.1三角形边角关系课件(共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 766.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-25 09:44:11 | ||
图片预览


文档简介
(共15张PPT)
第一课时
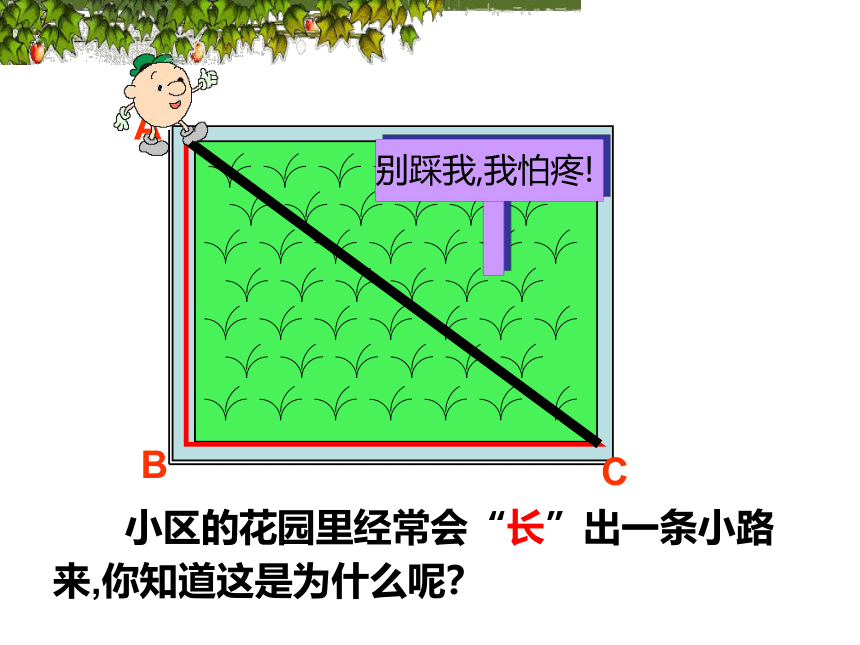
小区的花园里经常会“长”出一条小路来,你知道这是为什么呢?
别踩我,我怕疼!
A
B
C
三角形的定义:
由不在同一条直线上的三条线段首尾依次相接所组成的图形,叫做三角形.
B
C
A
三角形用符号“△”表示,
如图,三角形ABC,
读作:
△ ABC,
三角形ABC.
记作:
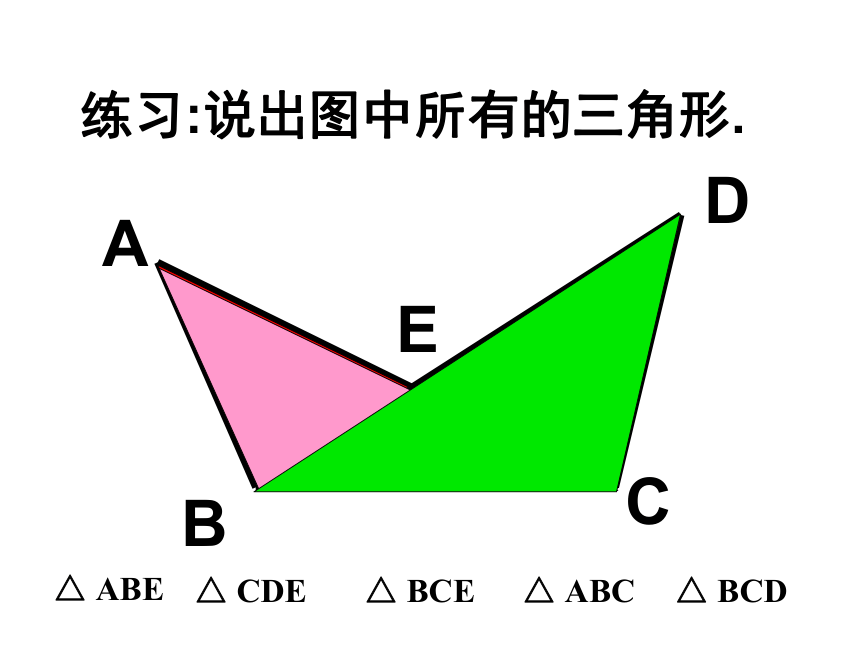
练习:说出图中所有的三角形.
A
D
B
E
C
△ ABE
△ CDE
△ BCE
△ ABC
△ BCD
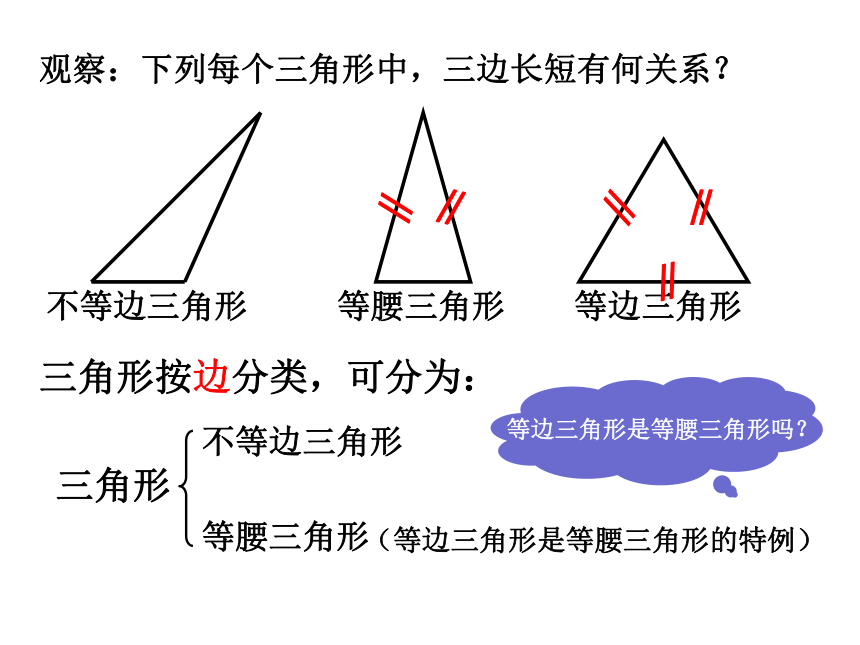
观察:下列每个三角形中,三边长短有何关系?
不等边三角形
等腰三角形
等边三角形
等边三角形是等腰三角形吗?
∥
∥
∥
∥
∥
三角形
不等边三角形
等腰三角形
(等边三角形是等腰三角形的特例)
三角形按边分类,可分为:
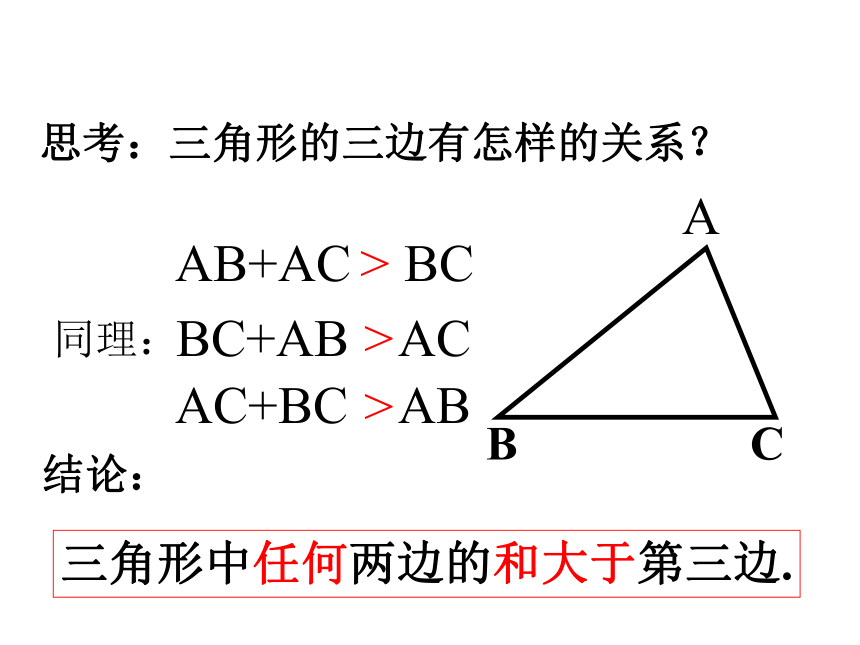
B
C
A
AB+AC BC
同理:
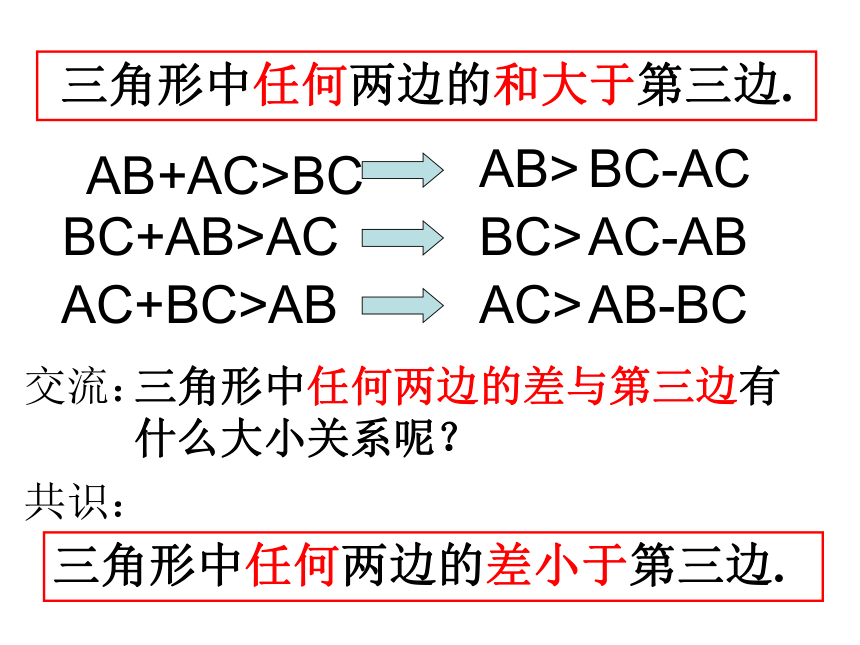
三角形中任何两边的和大于第三边.
思考:三角形的三边有怎样的关系?
AC+BC AB
BC+AB AC
>
>
结论:
>
AB+AC>BC
三角形中任何两边的差与第三边有什么大小关系呢?
三角形中任何两边的差小于第三边.
交流:
三角形中任何两边的和大于第三边.
AC+BC>AB
BC+AB>AC
AC>
BC>
AB>
BC-AC
AC-AB
AB-BC
共识:
1.某小区的花园里经常会“长”出一条小路来,你能不能运用今天所学的知识解释这一现象
其实我们离文明很近!
4
(假定小朋友1米=2步)
他只少走 步
4米
别踩我,我怕疼!
5米
A
B
C
3米
三角形中任何两边的和大于第三边.
能
不能
能
不能
若两条较短线段的和大于最长线段,则能构成三角形;若不满足,则不能构成三角形.
解题技巧:
2.判断:
用下列长度的3条线段能否组成一个 三角形?
①1cm,2cm,3cm.
②2cm,3cm,4cm.
③4cm,5cm,6cm.
④4cm,5cm,10cm.
(1)如果腰长是底边长的2倍,求各边长.
答:此三角形的各边长分别是7.2cm、7.2cm、3.6cm。
已知:等腰三角形中,周长是18cm,
解:
设底边长为xcm,则腰为2xcm,根据题意得:
2x+2x+x=18
解得:
x=3.6
7.2
∴腰长2x=
(2)如果一边长为4cm,求另两边长.
已知:等腰三角形中,周长是18cm,
解:
若底边长为4cm,设腰长为xcm,则有
2x+4=18
解得:x =7
若一条腰长为4cm,设底边长为xcm,则有
解得:x =10
因为4+4<10,
所以,以4cm为一腰不能构成三角形.
所以,三角形的另两边长都是7cm.
“一边长”是指哪边长?底边还是腰?
所以三角形的另两边长是7cm、 7cm或4cm、10cm.
小颖要制作一个三角形木架,现有两根长度为8cm和5cm的木棒,如果要求第三根木棒的长度是偶数,小颖有几种选法?第三根的长度可以是多少?
∴小颖有5种选法.
第三根木棒的长度可以是:
解:设第三根木棒的长度是x cm.则
3< x <13
∵X是偶数
4cm,6cm,8cm,10cm,12cm.
8+5 > x
8-5 < x
解得:
通过本节课的学习,你有哪些收获?
2017年6月17日
本节课我们认识了生活中最基本的几何图形—— ,通过观察、画图,了解了它的概念与基本元素,以及用符号“△”把它表示出来,并且能够按边对它进行分类,分为 和 ;根据上学期所学的几何知识“两点之间, ”,又结合实验操作得出结论:三角形中任何两边的和 ;然后利用不等式的性质进行了交流,获得共识:三角形中任何两边的差 .
通过练习,掌握了判断三条线段能否构成三角形的简便方法: ;并且能够根据三角形已知的两条边的长,来确定第三边的取值范围: .
三角形
不等边三角形
等腰三角形
线段最短
大于第三边
小于第三边
若两条较短线段的和大于最长线段,则能构成三角形
第三边大于其他两边的差,小于其他两边的和
1.必做:
教材69页练习1、3;习题13.1第1题.
2.选做:
自制不同形状的三角形模型.
祝同学们在以后的学习中:
一帆风顺 ,万事如意!
第一课时
小区的花园里经常会“长”出一条小路来,你知道这是为什么呢?
别踩我,我怕疼!
A
B
C
三角形的定义:
由不在同一条直线上的三条线段首尾依次相接所组成的图形,叫做三角形.
B
C
A
三角形用符号“△”表示,
如图,三角形ABC,
读作:
△ ABC,
三角形ABC.
记作:
练习:说出图中所有的三角形.
A
D
B
E
C
△ ABE
△ CDE
△ BCE
△ ABC
△ BCD
观察:下列每个三角形中,三边长短有何关系?
不等边三角形
等腰三角形
等边三角形
等边三角形是等腰三角形吗?
∥
∥
∥
∥
∥
三角形
不等边三角形
等腰三角形
(等边三角形是等腰三角形的特例)
三角形按边分类,可分为:
B
C
A
AB+AC BC
同理:
三角形中任何两边的和大于第三边.
思考:三角形的三边有怎样的关系?
AC+BC AB
BC+AB AC
>
>
结论:
>
AB+AC>BC
三角形中任何两边的差与第三边有什么大小关系呢?
三角形中任何两边的差小于第三边.
交流:
三角形中任何两边的和大于第三边.
AC+BC>AB
BC+AB>AC
AC>
BC>
AB>
BC-AC
AC-AB
AB-BC
共识:
1.某小区的花园里经常会“长”出一条小路来,你能不能运用今天所学的知识解释这一现象
其实我们离文明很近!
4
(假定小朋友1米=2步)
他只少走 步
4米
别踩我,我怕疼!
5米
A
B
C
3米
三角形中任何两边的和大于第三边.
能
不能
能
不能
若两条较短线段的和大于最长线段,则能构成三角形;若不满足,则不能构成三角形.
解题技巧:
2.判断:
用下列长度的3条线段能否组成一个 三角形?
①1cm,2cm,3cm.
②2cm,3cm,4cm.
③4cm,5cm,6cm.
④4cm,5cm,10cm.
(1)如果腰长是底边长的2倍,求各边长.
答:此三角形的各边长分别是7.2cm、7.2cm、3.6cm。
已知:等腰三角形中,周长是18cm,
解:
设底边长为xcm,则腰为2xcm,根据题意得:
2x+2x+x=18
解得:
x=3.6
7.2
∴腰长2x=
(2)如果一边长为4cm,求另两边长.
已知:等腰三角形中,周长是18cm,
解:
若底边长为4cm,设腰长为xcm,则有
2x+4=18
解得:x =7
若一条腰长为4cm,设底边长为xcm,则有
解得:x =10
因为4+4<10,
所以,以4cm为一腰不能构成三角形.
所以,三角形的另两边长都是7cm.
“一边长”是指哪边长?底边还是腰?
所以三角形的另两边长是7cm、 7cm或4cm、10cm.
小颖要制作一个三角形木架,现有两根长度为8cm和5cm的木棒,如果要求第三根木棒的长度是偶数,小颖有几种选法?第三根的长度可以是多少?
∴小颖有5种选法.
第三根木棒的长度可以是:
解:设第三根木棒的长度是x cm.则
3< x <13
∵X是偶数
4cm,6cm,8cm,10cm,12cm.
8+5 > x
8-5 < x
解得:
通过本节课的学习,你有哪些收获?
2017年6月17日
本节课我们认识了生活中最基本的几何图形—— ,通过观察、画图,了解了它的概念与基本元素,以及用符号“△”把它表示出来,并且能够按边对它进行分类,分为 和 ;根据上学期所学的几何知识“两点之间, ”,又结合实验操作得出结论:三角形中任何两边的和 ;然后利用不等式的性质进行了交流,获得共识:三角形中任何两边的差 .
通过练习,掌握了判断三条线段能否构成三角形的简便方法: ;并且能够根据三角形已知的两条边的长,来确定第三边的取值范围: .
三角形
不等边三角形
等腰三角形
线段最短
大于第三边
小于第三边
若两条较短线段的和大于最长线段,则能构成三角形
第三边大于其他两边的差,小于其他两边的和
1.必做:
教材69页练习1、3;习题13.1第1题.
2.选做:
自制不同形状的三角形模型.
祝同学们在以后的学习中:
一帆风顺 ,万事如意!
