人教版数学八下第3话平行四边形、矩形综合学案
文档属性
| 名称 | 人教版数学八下第3话平行四边形、矩形综合学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 324.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-25 17:41:53 | ||
图片预览


文档简介
第3话:平行四边形、矩形综合
课堂思维碰撞
第一层:平行四边形进阶
知识导入
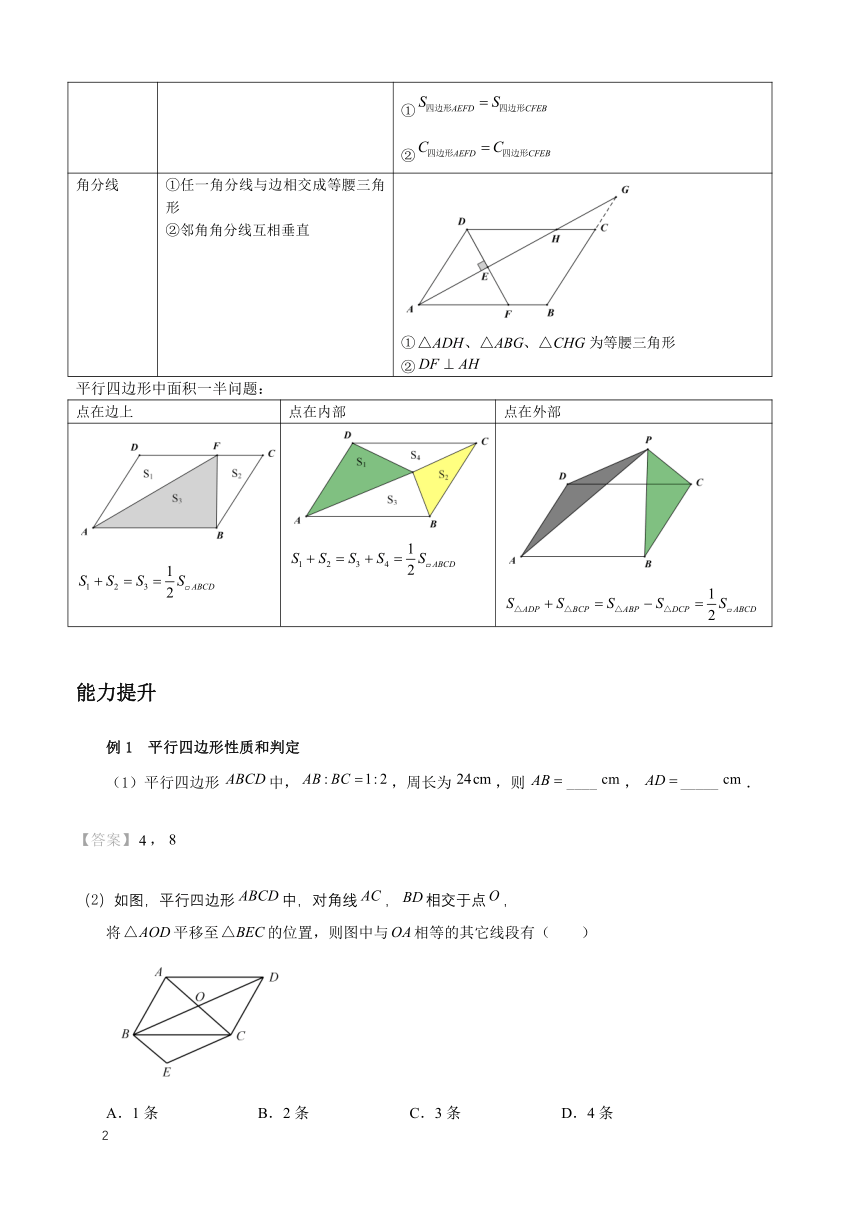
性质 图解
边 ①两组对边分别平行且相等 ①, ②,, ③, ④ ⑤,
角 ②对角相等,邻角互补
对角线 ③对角线互相平分 ④分成的四个小三角形面积相等 其中两对小三角形全等 ⑤对角线交点为平行四边形对称中心
周长 ①周长=邻边之和×2 ① ②
面积 ②面积=底×高
对称中心 ①过对称中心的直线把平行四边形分成全等两部分 ②过对称中心的直线平分平行四边形的面积和周长 ① ②
角分线 ①任一角分线与边相交成等腰三角形 ②邻角角分线互相垂直 ①为等腰三角形 ②
平行四边形中面积一半问题:
点在边上 点在内部 点在外部
能力提升
例1 平行四边形性质和判定
(1)平行四边形中,,周长为,则____,_____.
【答案】,
(2)如图,平行四边形中,对角线,相交于点,
将平移至的位置,则图中与相等的其它线段有( )
A.1条 B.2条 C.3条 D.4条
【答案】B(和)
(3)如图,在平行四边形中,,在上取,则________.
【答案】
(4)在四边形ABCD中,若有下列四个条件:
①AB∥CD;②AD=BC;③∠A=∠C;④AB=CD.
现以其中的两个条件为一组,能判定四边形ABCD是平行四边形的条件有( )
A.3组 B.4组 C.5组 D.6组
【答案】A
例2 平行四边形的模型
(1)如图,□ABCD中,∠ABC和∠BCD的平分线交于AD边上一点E,且BE⊥CE,若BE=4,CE=3,则□ABCD的面积是
【答案】12
(2)如图:是内的一点,,则=___________.
【答案】1:6
(3)如图,平行四边形的对角线相交于点,过点作交于,如果的周长为,那么平行四边形的周长为___________.
【答案】
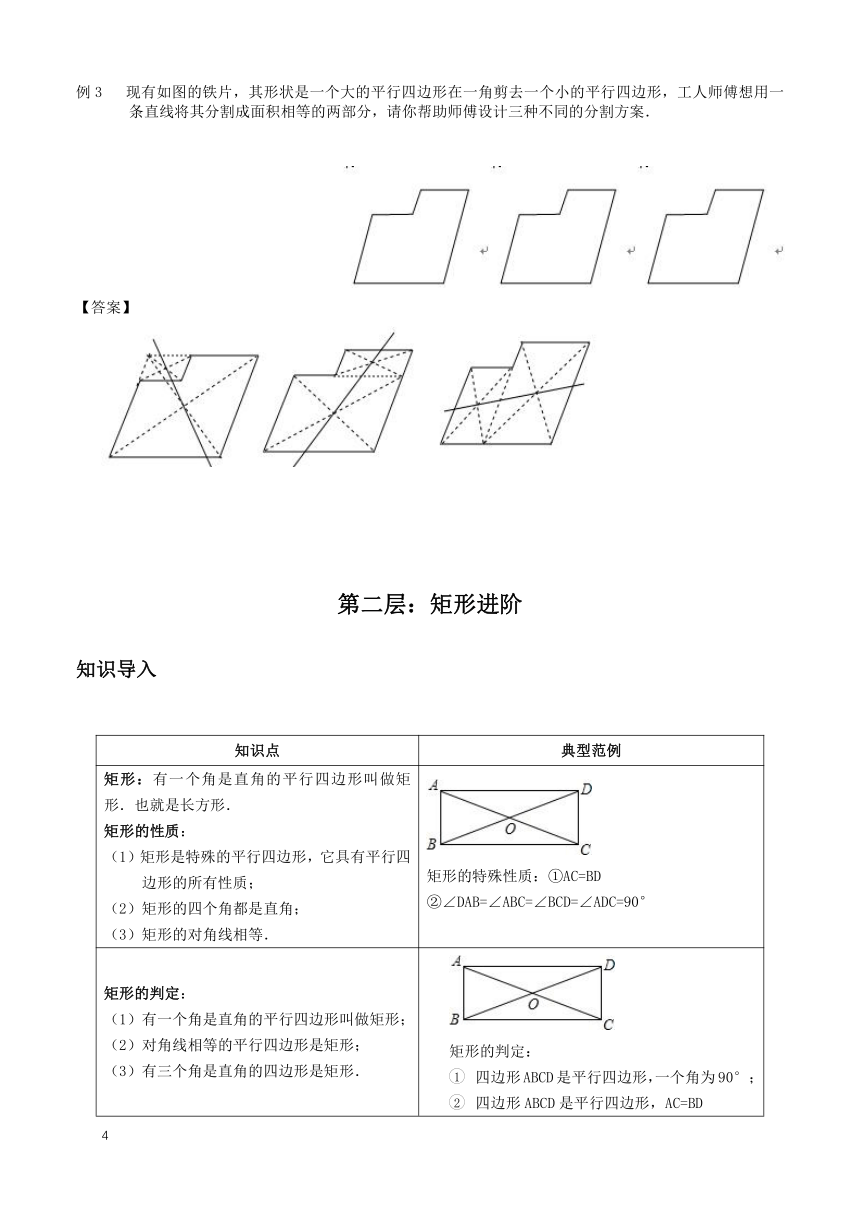
例3 现有如图的铁片,其形状是一个大的平行四边形在一角剪去一个小的平行四边形,工人师傅想用一条直线将其分割成面积相等的两部分,请你帮助师傅设计三种不同的分割方案.
【答案】
第二层:矩形进阶
知识导入
知识点 典型范例
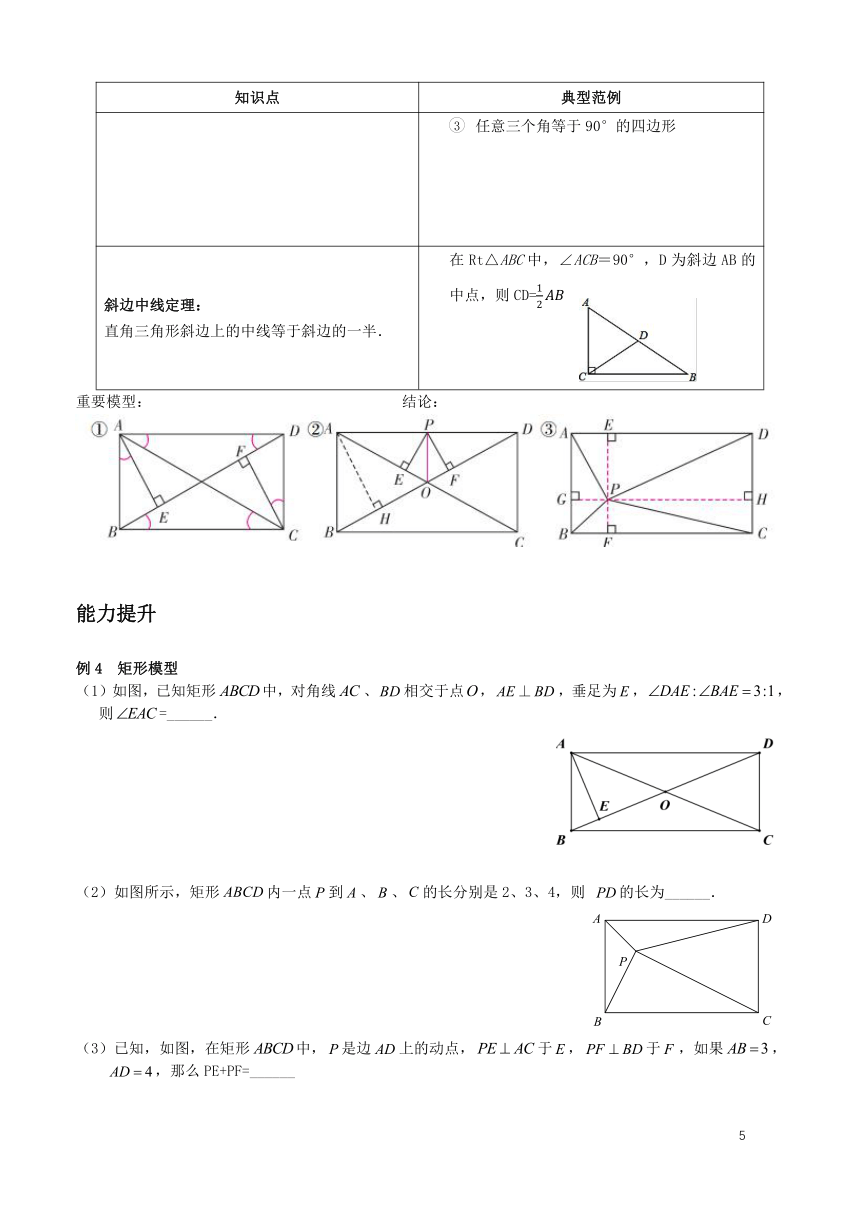
矩形:有一个角是直角的平行四边形叫做矩形.也就是长方形. 矩形的性质: (1)矩形是特殊的平行四边形,它具有平行四边形的所有性质; (2)矩形的四个角都是直角; (3)矩形的对角线相等. 矩形的特殊性质:①AC=BD ②∠DAB=∠ABC=∠BCD=∠ADC=90°
矩形的判定: (1)有一个角是直角的平行四边形叫做矩形; (2)对角线相等的平行四边形是矩形; (3)有三个角是直角的四边形是矩形. 矩形的判定: 四边形ABCD是平行四边形,一个角为90°; 四边形ABCD是平行四边形,AC=BD 任意三个角等于90°的四边形
斜边中线定理: 直角三角形斜边上的中线等于斜边的一半. 在Rt△ABC中,∠ACB=90°,D为斜边AB的中点,则CD=
重要模型: 结论:
能力提升
例4 矩形模型
(1)如图,已知矩形中,对角线、相交于点,,垂足为,,则=______.
(2)如图所示,矩形内一点到、、的长分别是2、3、4,则 的长为______.
(3)已知,如图,在矩形中,是边上的动点,于,于,如果, ,那么PE+PF=______
【答案】(1);(2);(3)
例5 矩形折叠
(1)如图,把矩形沿对折后使两部分重合,若,则=( )
A. B. C. D.
【答案】B
(2)如图,已知矩形,将沿对角线折叠,记点的对应点为,若,则的度数为________.
【答案】
(3)已知,如图所示,折叠长方形的一边,使点落在边的点处,如果,,求的长.
【解析】由题意得,.
在中,应用勾股定理得,
.
所以.
在中,应用勾股定理,设,得
.
解得 即.
(4)如图,将长方形纸片折叠,使边落在对角线上,折痕为,且点落在处,若,,则的长为( )
A. B.3 C.1 D.
【答案】A
(5)如图,将一个边长分别为4、8的长方形纸片折叠,使点与点重合,则AECF的面积为________.
【答案】 20
横扫学霸
例6 如图,在四边形中,,,,、两点在边上,且四边形是平行四边形.
⑴与有何等量关系?请说明理由;
⑵当时,求证:平行四边形是矩形.
【答案】⑴ 解:.
理由如下:
∵,,,
∴四边形和四边形都是平行四边形.
∴,.
又四边形是平行四边形,
∴.
∴.
∴.
⑵ 证明:四边形和四边形都是平行四边形,
∴,.
∵,
∴.
又∵四边形是平行四边形,
∴四边形是矩形.
课后创新培养
课后作业
练1 如图,在 ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=3,EF=1,则BC长为( )
A.4 B.5 C.6 D.7
【答案】B
练2 已知P是平行四边形ABCD内一点,若S△ABP:SABCD=2:5,则S△CPD:SABCD=_______
【答案】1:10
练3 如图,将矩形沿折叠,若则________.
【答案】
练4 如图,将矩形纸片ABCD沿直线EF折叠,使点C落在AD边的中点C′处,点B落在点B′处,其中AB=9,BC=6,则FC′的长为________
【答案】5
练5 如图,在 ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F,连接BD.
(1)求证:△ABE≌△CDF;
(2)若AB=DB,求证:四边形DFBE是矩形.
【答案】证明:(1)在□ABCD中,AB=CD,∠A=∠C.
∵AB∥CD,
∴∠ABD=∠CDB.
∵BE平分∠ABD,DF平分∠CDB,
∴∠ABE=∠ABD,∠CDF=∠CDB.
∴∠ABE=∠CDF.
∵在△ABE和△CDF中,
∴△ABE≌△CDF(ASA).
(2)∵△ABE≌△CDF,
∴AE=CF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴DE∥BF,DE=BF,
∴四边形DFBE是平行四边形,
∵AB=DB,BE平分∠ABD,
∴BE⊥AD,即∠DEB=90°.
∴平行四边形DFBE是矩形.
4
5
课堂思维碰撞
第一层:平行四边形进阶
知识导入
性质 图解
边 ①两组对边分别平行且相等 ①, ②,, ③, ④ ⑤,
角 ②对角相等,邻角互补
对角线 ③对角线互相平分 ④分成的四个小三角形面积相等 其中两对小三角形全等 ⑤对角线交点为平行四边形对称中心
周长 ①周长=邻边之和×2 ① ②
面积 ②面积=底×高
对称中心 ①过对称中心的直线把平行四边形分成全等两部分 ②过对称中心的直线平分平行四边形的面积和周长 ① ②
角分线 ①任一角分线与边相交成等腰三角形 ②邻角角分线互相垂直 ①为等腰三角形 ②
平行四边形中面积一半问题:
点在边上 点在内部 点在外部
能力提升
例1 平行四边形性质和判定
(1)平行四边形中,,周长为,则____,_____.
【答案】,
(2)如图,平行四边形中,对角线,相交于点,
将平移至的位置,则图中与相等的其它线段有( )
A.1条 B.2条 C.3条 D.4条
【答案】B(和)
(3)如图,在平行四边形中,,在上取,则________.
【答案】
(4)在四边形ABCD中,若有下列四个条件:
①AB∥CD;②AD=BC;③∠A=∠C;④AB=CD.
现以其中的两个条件为一组,能判定四边形ABCD是平行四边形的条件有( )
A.3组 B.4组 C.5组 D.6组
【答案】A
例2 平行四边形的模型
(1)如图,□ABCD中,∠ABC和∠BCD的平分线交于AD边上一点E,且BE⊥CE,若BE=4,CE=3,则□ABCD的面积是
【答案】12
(2)如图:是内的一点,,则=___________.
【答案】1:6
(3)如图,平行四边形的对角线相交于点,过点作交于,如果的周长为,那么平行四边形的周长为___________.
【答案】
例3 现有如图的铁片,其形状是一个大的平行四边形在一角剪去一个小的平行四边形,工人师傅想用一条直线将其分割成面积相等的两部分,请你帮助师傅设计三种不同的分割方案.
【答案】
第二层:矩形进阶
知识导入
知识点 典型范例
矩形:有一个角是直角的平行四边形叫做矩形.也就是长方形. 矩形的性质: (1)矩形是特殊的平行四边形,它具有平行四边形的所有性质; (2)矩形的四个角都是直角; (3)矩形的对角线相等. 矩形的特殊性质:①AC=BD ②∠DAB=∠ABC=∠BCD=∠ADC=90°
矩形的判定: (1)有一个角是直角的平行四边形叫做矩形; (2)对角线相等的平行四边形是矩形; (3)有三个角是直角的四边形是矩形. 矩形的判定: 四边形ABCD是平行四边形,一个角为90°; 四边形ABCD是平行四边形,AC=BD 任意三个角等于90°的四边形
斜边中线定理: 直角三角形斜边上的中线等于斜边的一半. 在Rt△ABC中,∠ACB=90°,D为斜边AB的中点,则CD=
重要模型: 结论:
能力提升
例4 矩形模型
(1)如图,已知矩形中,对角线、相交于点,,垂足为,,则=______.
(2)如图所示,矩形内一点到、、的长分别是2、3、4,则 的长为______.
(3)已知,如图,在矩形中,是边上的动点,于,于,如果, ,那么PE+PF=______
【答案】(1);(2);(3)
例5 矩形折叠
(1)如图,把矩形沿对折后使两部分重合,若,则=( )
A. B. C. D.
【答案】B
(2)如图,已知矩形,将沿对角线折叠,记点的对应点为,若,则的度数为________.
【答案】
(3)已知,如图所示,折叠长方形的一边,使点落在边的点处,如果,,求的长.
【解析】由题意得,.
在中,应用勾股定理得,
.
所以.
在中,应用勾股定理,设,得
.
解得 即.
(4)如图,将长方形纸片折叠,使边落在对角线上,折痕为,且点落在处,若,,则的长为( )
A. B.3 C.1 D.
【答案】A
(5)如图,将一个边长分别为4、8的长方形纸片折叠,使点与点重合,则AECF的面积为________.
【答案】 20
横扫学霸
例6 如图,在四边形中,,,,、两点在边上,且四边形是平行四边形.
⑴与有何等量关系?请说明理由;
⑵当时,求证:平行四边形是矩形.
【答案】⑴ 解:.
理由如下:
∵,,,
∴四边形和四边形都是平行四边形.
∴,.
又四边形是平行四边形,
∴.
∴.
∴.
⑵ 证明:四边形和四边形都是平行四边形,
∴,.
∵,
∴.
又∵四边形是平行四边形,
∴四边形是矩形.
课后创新培养
课后作业
练1 如图,在 ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=3,EF=1,则BC长为( )
A.4 B.5 C.6 D.7
【答案】B
练2 已知P是平行四边形ABCD内一点,若S△ABP:SABCD=2:5,则S△CPD:SABCD=_______
【答案】1:10
练3 如图,将矩形沿折叠,若则________.
【答案】
练4 如图,将矩形纸片ABCD沿直线EF折叠,使点C落在AD边的中点C′处,点B落在点B′处,其中AB=9,BC=6,则FC′的长为________
【答案】5
练5 如图,在 ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F,连接BD.
(1)求证:△ABE≌△CDF;
(2)若AB=DB,求证:四边形DFBE是矩形.
【答案】证明:(1)在□ABCD中,AB=CD,∠A=∠C.
∵AB∥CD,
∴∠ABD=∠CDB.
∵BE平分∠ABD,DF平分∠CDB,
∴∠ABE=∠ABD,∠CDF=∠CDB.
∴∠ABE=∠CDF.
∵在△ABE和△CDF中,
∴△ABE≌△CDF(ASA).
(2)∵△ABE≌△CDF,
∴AE=CF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴DE∥BF,DE=BF,
∴四边形DFBE是平行四边形,
∵AB=DB,BE平分∠ABD,
∴BE⊥AD,即∠DEB=90°.
∴平行四边形DFBE是矩形.
4
5
