人教版数学八下第8话一次函数存在性问题之距离学案
文档属性
| 名称 | 人教版数学八下第8话一次函数存在性问题之距离学案 | 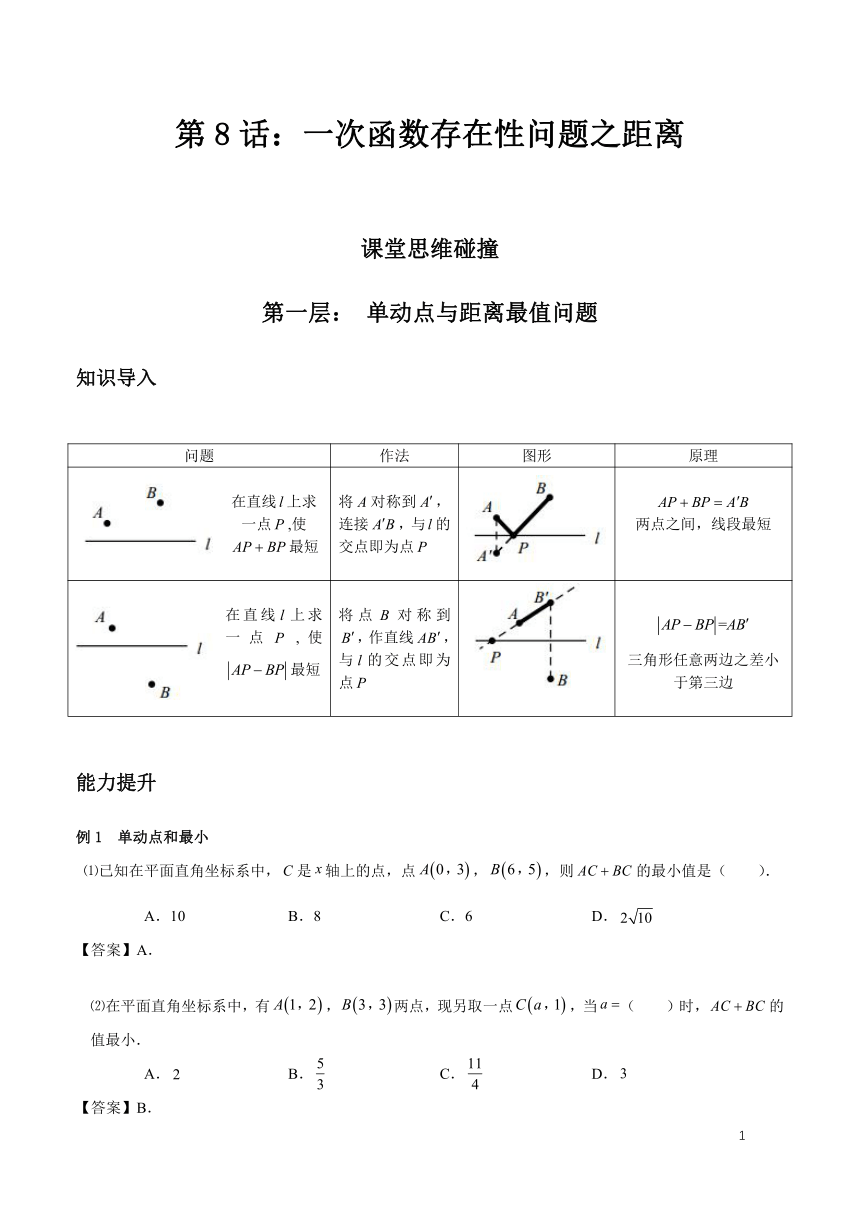 | |
| 格式 | zip | ||
| 文件大小 | 432.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-25 17:48:37 | ||
图片预览




文档简介
第8话:一次函数存在性问题之距离
课堂思维碰撞
第一层: 单动点与距离最值问题
知识导入
问题 作法 图形 原理
在直线上求一点,使最短 将对称到,连接,与的交点即为点 两点之间,线段最短
在直线上求一点,使最短 将点对称到,作直线,与的交点即为点 三角形任意两边之差小于第三边
能力提升
例1 单动点和最小
⑴已知在平面直角坐标系中,是轴上的点,点,,则的最小值是( ).
A.10 B.8 C.6 D.
【答案】A.
⑵在平面直角坐标系中,有,两点,现另取一点,当( )时,的值最小.
A. B. C. D.
【答案】B.
例2 单动点差最大
已知:直角坐标平面上两点,,
(1)若为轴上一点.求当的值最大时,点的坐标
(2)若为轴上一点.求当的值最大时,点的坐标
【答案】
解:(1)
(2)
例3 点、均在由面积为1的相同小正方形组成的网格的格点上,建立平面直角坐标系如图所示.若是轴上使得的值最大的点,是轴上使得的值最小的点,则的值为多少?
【答案】5
第二层: 双动点与距离最值问题
知识导入
能力提升
例4 如图,在轴上一点,在轴上找一点,使四边形ABCD的周长为最小值,求这个最值.
【答案】如图,.
例5 在直角坐标系中,有点A(0,1),B(5,3),点M、N在x轴上且MN=1,当四边形AMNB周长最短时,求点M、N的坐标.
【答案】M(1,0),N(2,0)
例6 将一矩形纸片OABC放在平面直角坐标系中,O为原点,点A在x轴上,点C在y轴上,OA=10,OC=8,如图在OC边上取一点D,将△BCD沿BD折叠,使点C恰好落在OA边上,记作E点;
(1)求点E的坐标及折痕DB的长;
(2)在x轴上取两点M、N(点M在点N的左侧),且MN=4.5,求使四边形BDMN的周长最短的点M、点N的坐标.
【答案】解:(1)∵四边形OABC为矩形,
∴BC=OA=10,AB=OC=8,
∵△BCD沿BD折叠,使点C恰好落在OA边E点上,
∴BC=BE=10,DC=DE,
在Rt△ABE中,BE=10,AB=8,
∴AE=6,
∴OE=10﹣6=4,
∴E点坐标为(4,0);
在Rt△ODE中,设DE=x,则OD=OC﹣DC=OC﹣DE=8﹣x,
∴x2=42+(8﹣x)2,解得x=5,
在Rt△BDE中,
BD==5;
(2)以D、M、N为顶点作平行四边形DMND′,作出点B关于x轴对称点B′,如图,
∴B′的坐标为(10,﹣8),DD′=MN=4.5,∴D′的坐标为(4.5,3),
设直线D′B′的解析式为y=kx+b,
把B′(10,﹣8),D′(4.5,3)代入得,10k+b=﹣8,4.5k+b=3,解得k=﹣2,b=12,
∴直线D′B′的解析式为y=﹣2x+12,
令y=0,得﹣2x+12=0,解得x=6,
∴M(1.5,0);N(6,0).
第三层: 特殊动点问题
能力提升
例7 已知平面直角坐标系中,存在点,已知点E、F分别为直线y=x和x轴上的动点.
(1)求的周长最小值;
(2)求的最小值.
【答案】(1)如图,分别过y=x和x轴作A的对称点和
连接,与 y=x和x轴的交点即为当的周长最小时,E、F的位置 ,此时
(2)如图,AE+EF最短,即过y=x作A的对称点,再过作x轴的垂线, 与 y=x和x轴的交点即为最小时,E、F的位置 ,此时AE+EF=4
课后创新培养
课后作业
练1 ⑴在平面直角坐标系中,轴上的动点到点、的距离分别为、,求当最小时的点坐标是( ).
A. B. C. D.
【答案】B.
⑵在直角坐标系中,已知点,,在轴上找一点,使最短,则点的坐标为( ).
A. B. C. D.
【答案】B.
练2 在平面直角坐标系中,已知、,是轴上一点,当的坐标为________,取最小值,最小值为____________;当的坐标为________,取最大值,最大值为________.
【答案】,;,.
练3 在直角坐标系中,有四个点、、、,当四边形的周长最小时,的值为_________.
【答案】由、两点固定可知,的线段长度固定,故只需考虑的长度,取点B关于轴的对称点、点关于轴的对称点,易知当、、、四点共线时,的长度最小,最小值为. 易知直线的解析式为:,此时、,故.
练4 已知点A(3,4)点,在轴上另取两点,,且.线段在轴上平移,线段平移至何处时,四边形的周长最小?求出此时点的坐标.
【答案】如图2,过点作轴的平行线,并且在这条平行线上截取线段,使,作点关于轴的对称点,连接,交轴于点,在轴上截取线段,则此时四边形的周长最小.
∵,∴,
∵,∴.
设直线的解析式为,
则,
解得.
∴直线的解析式为,
当时,,解得.
故线段平移至如图所示位置时,四边形的周长最小,此时点的坐标为.
8
7
课堂思维碰撞
第一层: 单动点与距离最值问题
知识导入
问题 作法 图形 原理
在直线上求一点,使最短 将对称到,连接,与的交点即为点 两点之间,线段最短
在直线上求一点,使最短 将点对称到,作直线,与的交点即为点 三角形任意两边之差小于第三边
能力提升
例1 单动点和最小
⑴已知在平面直角坐标系中,是轴上的点,点,,则的最小值是( ).
A.10 B.8 C.6 D.
【答案】A.
⑵在平面直角坐标系中,有,两点,现另取一点,当( )时,的值最小.
A. B. C. D.
【答案】B.
例2 单动点差最大
已知:直角坐标平面上两点,,
(1)若为轴上一点.求当的值最大时,点的坐标
(2)若为轴上一点.求当的值最大时,点的坐标
【答案】
解:(1)
(2)
例3 点、均在由面积为1的相同小正方形组成的网格的格点上,建立平面直角坐标系如图所示.若是轴上使得的值最大的点,是轴上使得的值最小的点,则的值为多少?
【答案】5
第二层: 双动点与距离最值问题
知识导入
能力提升
例4 如图,在轴上一点,在轴上找一点,使四边形ABCD的周长为最小值,求这个最值.
【答案】如图,.
例5 在直角坐标系中,有点A(0,1),B(5,3),点M、N在x轴上且MN=1,当四边形AMNB周长最短时,求点M、N的坐标.
【答案】M(1,0),N(2,0)
例6 将一矩形纸片OABC放在平面直角坐标系中,O为原点,点A在x轴上,点C在y轴上,OA=10,OC=8,如图在OC边上取一点D,将△BCD沿BD折叠,使点C恰好落在OA边上,记作E点;
(1)求点E的坐标及折痕DB的长;
(2)在x轴上取两点M、N(点M在点N的左侧),且MN=4.5,求使四边形BDMN的周长最短的点M、点N的坐标.
【答案】解:(1)∵四边形OABC为矩形,
∴BC=OA=10,AB=OC=8,
∵△BCD沿BD折叠,使点C恰好落在OA边E点上,
∴BC=BE=10,DC=DE,
在Rt△ABE中,BE=10,AB=8,
∴AE=6,
∴OE=10﹣6=4,
∴E点坐标为(4,0);
在Rt△ODE中,设DE=x,则OD=OC﹣DC=OC﹣DE=8﹣x,
∴x2=42+(8﹣x)2,解得x=5,
在Rt△BDE中,
BD==5;
(2)以D、M、N为顶点作平行四边形DMND′,作出点B关于x轴对称点B′,如图,
∴B′的坐标为(10,﹣8),DD′=MN=4.5,∴D′的坐标为(4.5,3),
设直线D′B′的解析式为y=kx+b,
把B′(10,﹣8),D′(4.5,3)代入得,10k+b=﹣8,4.5k+b=3,解得k=﹣2,b=12,
∴直线D′B′的解析式为y=﹣2x+12,
令y=0,得﹣2x+12=0,解得x=6,
∴M(1.5,0);N(6,0).
第三层: 特殊动点问题
能力提升
例7 已知平面直角坐标系中,存在点,已知点E、F分别为直线y=x和x轴上的动点.
(1)求的周长最小值;
(2)求的最小值.
【答案】(1)如图,分别过y=x和x轴作A的对称点和
连接,与 y=x和x轴的交点即为当的周长最小时,E、F的位置 ,此时
(2)如图,AE+EF最短,即过y=x作A的对称点,再过作x轴的垂线, 与 y=x和x轴的交点即为最小时,E、F的位置 ,此时AE+EF=4
课后创新培养
课后作业
练1 ⑴在平面直角坐标系中,轴上的动点到点、的距离分别为、,求当最小时的点坐标是( ).
A. B. C. D.
【答案】B.
⑵在直角坐标系中,已知点,,在轴上找一点,使最短,则点的坐标为( ).
A. B. C. D.
【答案】B.
练2 在平面直角坐标系中,已知、,是轴上一点,当的坐标为________,取最小值,最小值为____________;当的坐标为________,取最大值,最大值为________.
【答案】,;,.
练3 在直角坐标系中,有四个点、、、,当四边形的周长最小时,的值为_________.
【答案】由、两点固定可知,的线段长度固定,故只需考虑的长度,取点B关于轴的对称点、点关于轴的对称点,易知当、、、四点共线时,的长度最小,最小值为. 易知直线的解析式为:,此时、,故.
练4 已知点A(3,4)点,在轴上另取两点,,且.线段在轴上平移,线段平移至何处时,四边形的周长最小?求出此时点的坐标.
【答案】如图2,过点作轴的平行线,并且在这条平行线上截取线段,使,作点关于轴的对称点,连接,交轴于点,在轴上截取线段,则此时四边形的周长最小.
∵,∴,
∵,∴.
设直线的解析式为,
则,
解得.
∴直线的解析式为,
当时,,解得.
故线段平移至如图所示位置时,四边形的周长最小,此时点的坐标为.
8
7
