人教版数学八下第10话一次函数存在性问题之几何图形综合学案
文档属性
| 名称 | 人教版数学八下第10话一次函数存在性问题之几何图形综合学案 |  | |
| 格式 | zip | ||
| 文件大小 | 300.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-25 17:50:09 | ||
图片预览



文档简介
第10话:一次函数存在性问题之几何综合
课堂思维碰撞
第一层: 一次函数与等腰三角形综合
知识导入
两圆一线:
问题:已知点和点,找一点,使得为等腰三角形.
方法:⑴以点为圆心,为半径作圆,圆上的所有点都满足条件;
⑵以点为圆心,为半径作圆,圆上的所有点都满足条件;
⑶作的垂直平分线,垂直平分线上的所有点都满足条件.
两点间距离公式:
点和点的距离.
能力提升
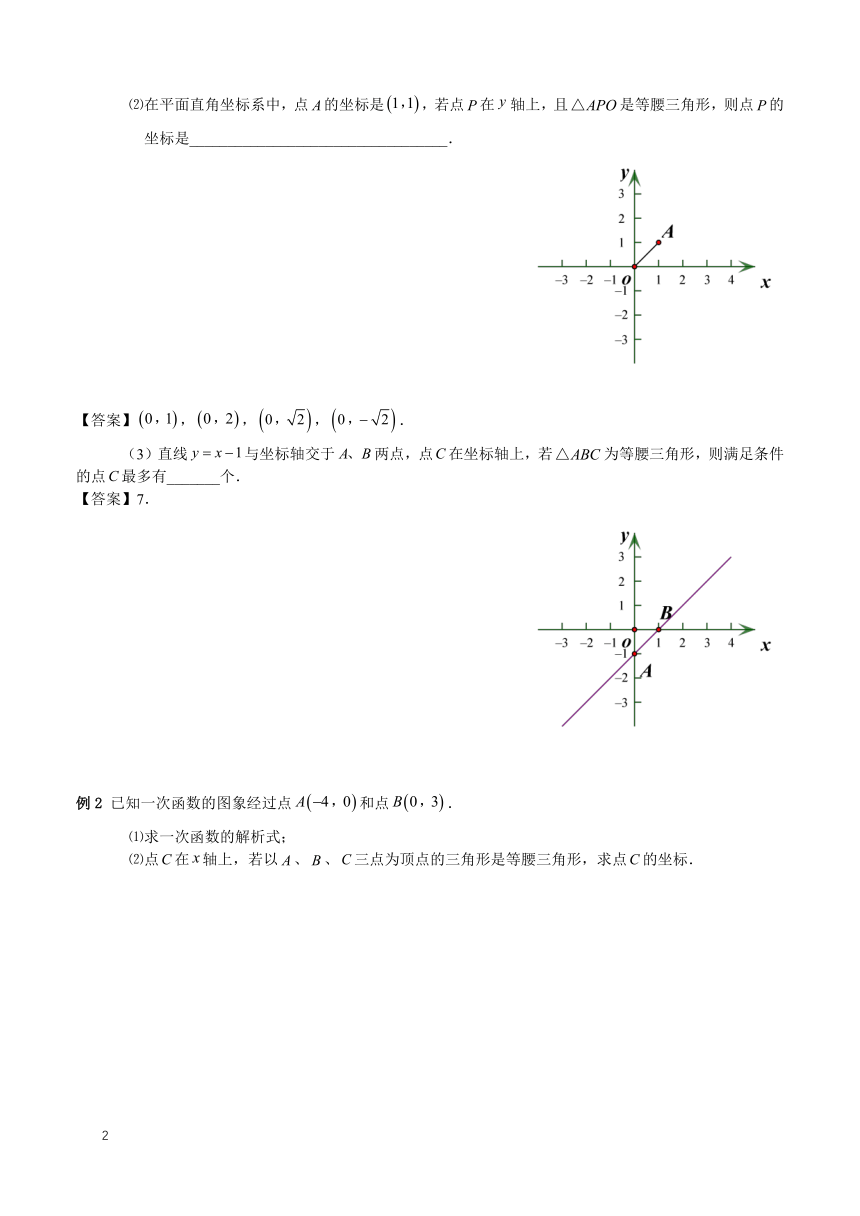
例1 ⑴在平面直角坐标系中,点的坐标是,若点在轴上,且是等腰三角形,则点的坐标是__________________________________.
【答案】,,,.
⑵在平面直角坐标系中,点的坐标是,若点在轴上,且是等腰三角形,则点的坐标是__________________________________.
【答案】,,,.
(3)直线与坐标轴交于两点,点在坐标轴上,若为等腰三角形,则满足条件的点最多有_______个.
【答案】7.
例2 已知一次函数的图象经过点和点.
⑴求一次函数的解析式;
⑵点在轴上,若以、、三点为顶点的三角形是等腰三角形,求点的坐标.
【答案】⑴设一次函数的解析式为
∵一次函数的图象经过点和点
∴
解得
∴一次函数的解析式为.
⑵∵,
∴
设点的坐标为
若,则点的坐标为和
若,则点的坐标为
若,则有,,.
例3 已知一次函数与轴、轴分别交于两点,点在x轴上,若是等腰三角形,则求满足条件的点的坐标.
【答案】,,,
第二层: 一次函数与平行四边形综合
能力提升
例4 (1)在平面直角坐标系中,、、三点的坐标分别为,,,以这三点为平行四边形的三个顶点,则第四个顶点不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】A
(2)在平面直角坐标系中若△ABC的顶点坐标分别为:A(3,0)、B(﹣1,0)、C(2,3)、若以点A、B、C、D为顶点的四边形是平行四边形,则点D的坐标为 .
【答案】解:当AB∥CD时,第4个顶点D的坐标是(﹣2,3)或(6,3),当AD∥BC时,第4个顶点D的坐标是(0,﹣3).
例5 如图,在平面直角坐标系中,直线分别交x轴、y轴于A、B两点.
(1)求A、B两点的坐标.
(2)设P是直线AB上一动点,直线PR∥x轴,点Q在直线PR上,设点P的横坐标为m,试用含有m的代数式表示点Q的纵坐标n.
(3)在(2)的条件下,若以B、O、Q、A为顶点的四边形是平行四边形,求此时点Q的坐标.
【解答】解:(1)当y=0时,x=3;
当x=0时,y=4,
所以点A(3,0),B(0,4);
(2)∵P点的横坐标为m,P在y=上,
∴P点纵坐标为,
∵Q在PR上,
∴Q点纵坐标;
(3)当OA为平行四边形一边时,BQ∥OA且BO=OA,
∴Q(﹣3,4)或(3,4),
当OA为平行四边形对角线时,OB∥AQ,且OB=AQ,
∴Q(3,﹣4),
∴符合条件的Q点坐标为(﹣3,4)或(3,4)或(3,﹣4).
横扫学霸
例6 如图,在平面直角坐标系中,点A(4,2),B(﹣1,﹣3),P是x轴上的一点,Q是y轴上的一点,若以点A,B,P,Q四点为顶点的四边形是平行四边形,求点Q的坐标.
【答案】解:如图所示,
当AB为边,①即当四边形ABQ2P2是平行四边形,所以AB=P2Q2,AP2=BQ2,
∵点A(4,2),B(﹣1,﹣3),
∴AB=5,则OP2=OQ2=5,
∴Q2点的坐标是:(0,﹣5),
②当四边形QPBA是平行四边形,所以AB=PQ,QA=PB,
∴Q点的坐标是:(0,5),
③当AB为对角线,即当四边形P1AQ1B是平行四边形,
所以AP1=Q1B,AQ1=BP1,
∴Q1点的坐标是:(0,﹣1).
综上所述:符合题意的点Q的坐标为:(0,﹣5)或(0,﹣1)或(0,5).
课后创新培养
课后作业
练1 点的坐标是,若点在轴上,且是等腰三角形,则点的坐标不可能是( ).
A. B. C. D.
【答案】B.
练2 如图,在平面直角坐标系中,直线与轴、轴分别相交于点、,点在轴上,若是等腰三角形,试求点的坐标.
【答案】,,,.
练3 点的坐标分别是、、,点在线段上运动,当为等腰三角形时,点的坐标为_____________.
【答案】,,,
练4 如图,在平面直角坐标系中,A(﹣2,5),B(﹣3,﹣1),C(1,﹣1),在坐标系中找一点D,使以A、B、C、D为顶点的四边形为平行四边形,则点D的坐标是 (2,5)或(﹣6,5)或(0,﹣7) .
【解答】解:∵两组对边分别平行的四边形是平行四边形,∴可以分以下三种情况分别求出D点的坐标:
①当AB∥CD,AD∥BC时,D点的坐标为(2,5);
②当AD∥BC,AC∥BD时,D点的坐标为(﹣6,5);
③当AB∥CD,AC∥CD时,D点的坐标为(0,﹣7).
故D点坐标为(2,5)或(﹣6,5)或(0,﹣7).
练5 已知直线和直线相交于点,
⑴ 若与轴交于点,与轴交于点,求的面积;
⑵ 若点与点、、能构成平行四边形,试写出点坐标(只需写出坐标,不必写解答过程)
【答案】⑴,
所以;
⑵、、.
6
5
课堂思维碰撞
第一层: 一次函数与等腰三角形综合
知识导入
两圆一线:
问题:已知点和点,找一点,使得为等腰三角形.
方法:⑴以点为圆心,为半径作圆,圆上的所有点都满足条件;
⑵以点为圆心,为半径作圆,圆上的所有点都满足条件;
⑶作的垂直平分线,垂直平分线上的所有点都满足条件.
两点间距离公式:
点和点的距离.
能力提升
例1 ⑴在平面直角坐标系中,点的坐标是,若点在轴上,且是等腰三角形,则点的坐标是__________________________________.
【答案】,,,.
⑵在平面直角坐标系中,点的坐标是,若点在轴上,且是等腰三角形,则点的坐标是__________________________________.
【答案】,,,.
(3)直线与坐标轴交于两点,点在坐标轴上,若为等腰三角形,则满足条件的点最多有_______个.
【答案】7.
例2 已知一次函数的图象经过点和点.
⑴求一次函数的解析式;
⑵点在轴上,若以、、三点为顶点的三角形是等腰三角形,求点的坐标.
【答案】⑴设一次函数的解析式为
∵一次函数的图象经过点和点
∴
解得
∴一次函数的解析式为.
⑵∵,
∴
设点的坐标为
若,则点的坐标为和
若,则点的坐标为
若,则有,,.
例3 已知一次函数与轴、轴分别交于两点,点在x轴上,若是等腰三角形,则求满足条件的点的坐标.
【答案】,,,
第二层: 一次函数与平行四边形综合
能力提升
例4 (1)在平面直角坐标系中,、、三点的坐标分别为,,,以这三点为平行四边形的三个顶点,则第四个顶点不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】A
(2)在平面直角坐标系中若△ABC的顶点坐标分别为:A(3,0)、B(﹣1,0)、C(2,3)、若以点A、B、C、D为顶点的四边形是平行四边形,则点D的坐标为 .
【答案】解:当AB∥CD时,第4个顶点D的坐标是(﹣2,3)或(6,3),当AD∥BC时,第4个顶点D的坐标是(0,﹣3).
例5 如图,在平面直角坐标系中,直线分别交x轴、y轴于A、B两点.
(1)求A、B两点的坐标.
(2)设P是直线AB上一动点,直线PR∥x轴,点Q在直线PR上,设点P的横坐标为m,试用含有m的代数式表示点Q的纵坐标n.
(3)在(2)的条件下,若以B、O、Q、A为顶点的四边形是平行四边形,求此时点Q的坐标.
【解答】解:(1)当y=0时,x=3;
当x=0时,y=4,
所以点A(3,0),B(0,4);
(2)∵P点的横坐标为m,P在y=上,
∴P点纵坐标为,
∵Q在PR上,
∴Q点纵坐标;
(3)当OA为平行四边形一边时,BQ∥OA且BO=OA,
∴Q(﹣3,4)或(3,4),
当OA为平行四边形对角线时,OB∥AQ,且OB=AQ,
∴Q(3,﹣4),
∴符合条件的Q点坐标为(﹣3,4)或(3,4)或(3,﹣4).
横扫学霸
例6 如图,在平面直角坐标系中,点A(4,2),B(﹣1,﹣3),P是x轴上的一点,Q是y轴上的一点,若以点A,B,P,Q四点为顶点的四边形是平行四边形,求点Q的坐标.
【答案】解:如图所示,
当AB为边,①即当四边形ABQ2P2是平行四边形,所以AB=P2Q2,AP2=BQ2,
∵点A(4,2),B(﹣1,﹣3),
∴AB=5,则OP2=OQ2=5,
∴Q2点的坐标是:(0,﹣5),
②当四边形QPBA是平行四边形,所以AB=PQ,QA=PB,
∴Q点的坐标是:(0,5),
③当AB为对角线,即当四边形P1AQ1B是平行四边形,
所以AP1=Q1B,AQ1=BP1,
∴Q1点的坐标是:(0,﹣1).
综上所述:符合题意的点Q的坐标为:(0,﹣5)或(0,﹣1)或(0,5).
课后创新培养
课后作业
练1 点的坐标是,若点在轴上,且是等腰三角形,则点的坐标不可能是( ).
A. B. C. D.
【答案】B.
练2 如图,在平面直角坐标系中,直线与轴、轴分别相交于点、,点在轴上,若是等腰三角形,试求点的坐标.
【答案】,,,.
练3 点的坐标分别是、、,点在线段上运动,当为等腰三角形时,点的坐标为_____________.
【答案】,,,
练4 如图,在平面直角坐标系中,A(﹣2,5),B(﹣3,﹣1),C(1,﹣1),在坐标系中找一点D,使以A、B、C、D为顶点的四边形为平行四边形,则点D的坐标是 (2,5)或(﹣6,5)或(0,﹣7) .
【解答】解:∵两组对边分别平行的四边形是平行四边形,∴可以分以下三种情况分别求出D点的坐标:
①当AB∥CD,AD∥BC时,D点的坐标为(2,5);
②当AD∥BC,AC∥BD时,D点的坐标为(﹣6,5);
③当AB∥CD,AC∥CD时,D点的坐标为(0,﹣7).
故D点坐标为(2,5)或(﹣6,5)或(0,﹣7).
练5 已知直线和直线相交于点,
⑴ 若与轴交于点,与轴交于点,求的面积;
⑵ 若点与点、、能构成平行四边形,试写出点坐标(只需写出坐标,不必写解答过程)
【答案】⑴,
所以;
⑵、、.
6
5
