人教版数学七下第1讲相交线与平行线综合学案
文档属性
| 名称 | 人教版数学七下第1讲相交线与平行线综合学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 338.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-25 18:12:34 | ||
图片预览



文档简介
第1讲 相交线与平行线综合
课堂思维碰撞
模块一:相交线综合
知识导入
1.在同一平面内,两条直线的位置关系:相交、平行.
注意:我们说的两条直线是指不重合的两条直线.
2.相交直线:
定义:两条直线只有一个公共点,我们称这两条直线为相交线.
如下图,如果直线与直线有公共点,则称直线与直线相交,为交点,其中一条直线是另一条直线的相交线.
性质:相交直线有且只有一个公共点.
3.对顶角:
定义:如果两个角有公共顶点,它们的两边互为反向延长线,具有这种位置关系的两个角叫做对顶角.
定义:两条直线相交成四个角中,有公共顶点而没有公共边的两个角叫做对顶角.如图中,和、和是对顶角.
性质:对顶角相等,如图中:,.
4.邻补角:
定义:两条直线相交所构成的四个角中,有公共顶点且有一条公共边的两个角互为邻补角.如上图,和,和,和,和互为邻补角.
定义:我们也可以说,如果两个角有一条公共边,并且它们的另外一边互为反向延长线,那么这两个角叫做邻补角.
性质:邻补角互补,如上图:,,,.
5.垂线:
如果两条直线相交所成的四个角中有一个是直角,那么就说这两条直线互相垂直,其中的一条直线是另一条直线的垂线,它们的交点为垂足.
如图,直线、互相垂直,垂足为点,记作“于”.
6.三线八角模型:
如图,直线、与相交,也称直线、被直线所截,形成了个小于平角的角,我们通常将这样的几何模型称为“三线八角”.
(1)同位角:两条直线被第三条直线所截,在两条被截直线同旁,在截线同侧的一对角叫做同位角.如上图中:∠1和∠5,形似英文字母“F”.
(2)内错角:两条直线被第三条直线所截,在两条被截直线内部,在截线两侧的一对角叫做内错角.如上图中:∠3和∠5,形似英文字母“Z”.
(3)同旁内角:两条直线被第三条直线所截,在两条被截直线内部,在截线同侧的一对角叫做同旁内角.如上图中:∠4和∠5,形似英文字母“U”.
夯实基础
例1 对顶角、邻补角
(1)如图,∠1和∠2是对顶角的图形是( )
A.甲 B.乙 C.丙 D.丁
(2)如图,∠1与∠2互为邻补角的是( )
A. B. C. D.
(3)如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC:∠EOD=1:2,则∠BOD等于( )
A.30° B.36° C.45° D.72°
(4)已知:如图所示,直线、、交于点,,,则的度数是 .
【答案】(1)C;(2)D;(3)A;(4)60°.
例2 垂直
(1)如图,直线AB、CD相交于点O,OE⊥CD,∠AOE=52°,则∠BOD等于( )
A.24° B.26° C.36° D.38°
(2)如图,已知直线AB,线段CO⊥AB于点O,,的度数为( )
A.15° B.25° C.30° D.45°
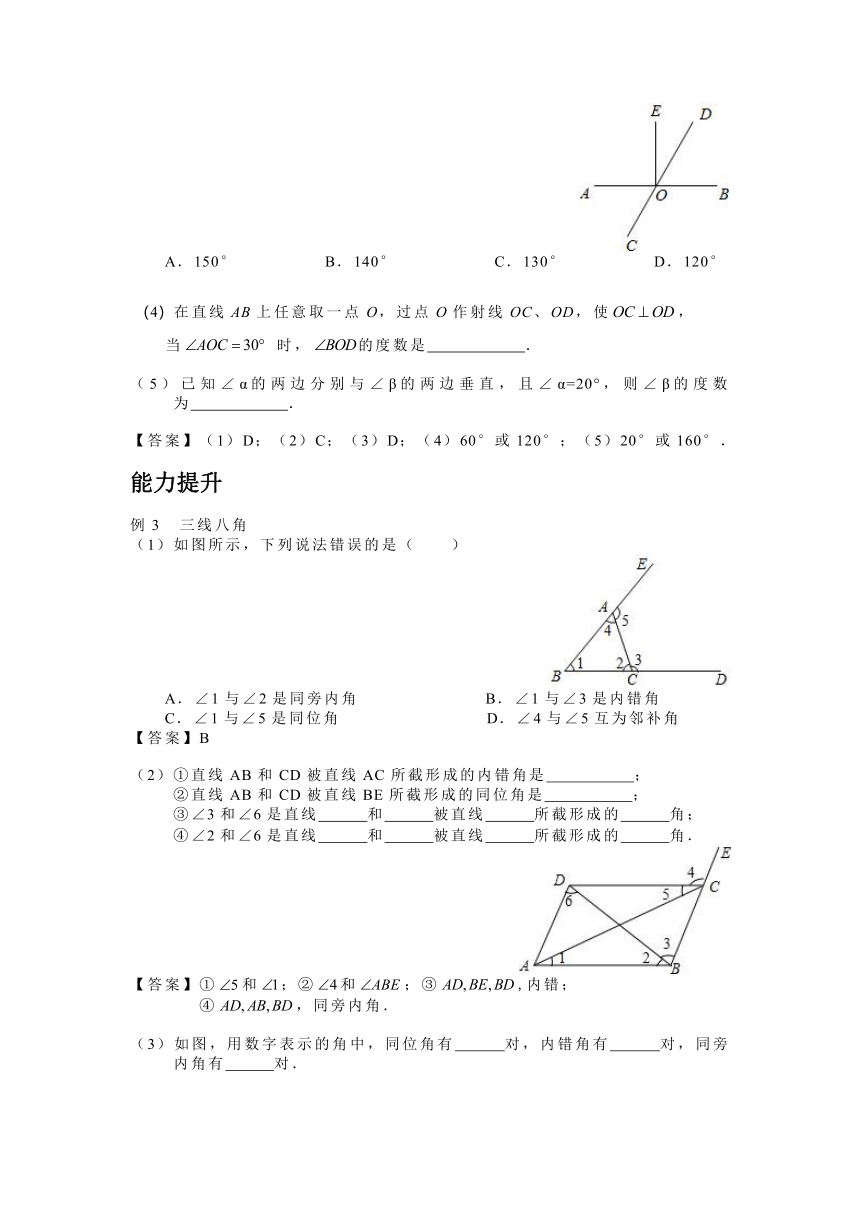
(3)如图,直线AB与直线CD相交于点O,OE⊥AB,垂足为O,,则( )
A.150° B.140° C.130° D.120°
(4)在直线AB上任意取一点O,过点O作射线OC、OD,使,当 时,的度数是 .
(5)已知∠α的两边分别与∠β的两边垂直,且∠α=20°,则∠β的度数为 .
【答案】(1)D;(2)C;(3)D;(4)60°或120°;(5)20°或160°.
能力提升
例3 三线八角
(1)如图所示,下列说法错误的是( )
A.∠1与∠2是同旁内角 B.∠1与∠3是内错角
C.∠1与∠5是同位角 D.∠4与∠5互为邻补角
【答案】B
(2)①直线AB和CD被直线AC所截形成的内错角是 ;
②直线AB和CD被直线BE所截形成的同位角是 ;
③∠3和∠6是直线 和 被直线 所截形成的 角;
④∠2和∠6是直线 和 被直线 所截形成的 角.
【答案】①和;②和;③,内错;
④,同旁内角.
(3)如图,用数字表示的角中,同位角有 对,内错角有 对,同旁内角有 对.
【答案】4,4,7.
例4 角度计算
(1)已知:∠MON=132°,射线OC是∠MON内一条射线,且,问OM与OC是否垂直,并说明理由.
(2)如图,,若∠BOC=4∠NOB,且OM平分∠NOC,求∠MON的度数.
【答案】(1),解出,∴.
(2)设,则有,解得:,∴.
模块二:平行线的性质判定进阶
知识导入
1.平行线的定义:
定义:在同一平面内,不相交的两条直线叫做平行线.
如图,如果直线与直线没有公共点,则称直线与直线平行,记作∥,读作平行于.
性质:平行直线在同一平面内,且没有公共点.
易错点:必须强调是在同一平面内.
2.平行线的性质:
性质1:两直线平行,同位角相等.
性质2:两直线平行,内错角相等.
性质3:两直线平行,同旁内角互补.
推论:①两直线平行,同位角的角平分线也平行.
②两直线平行,内错角的角平分线也平行.
③两直线平行,同旁内角的角平分线互相垂直.
3.平行线的判定:
(1)平行线的定义
(2)判定1:同位角相等,两直线平行.
(3)判定2:内错角相等,两直线平行.
(4)判定3:同旁内角互补,两直线平行.
推论:①两直线平行,同位角的角平分线也平行.
②两直线平行,内错角的角平分线也平行.
③两直线平行,同旁内角的角平分线互相垂直.
能力提升
例5 利用平行线性质计算角度
(1)如图,直线l1∥l2∥l3,点A、B、C分别在直线l1、l2、l3上,若∠1=72°,∠2=48°,则∠ABC=( )
A.24° B.120° C.96° D.132°
【答案】 B
(2)如图,,,,则______.
【答案】 20°.
(3)如图,AB∥CD∥EF,CB∥DE∥FG,如果∠1=70°,则∠3的度数为 .
【答案】110°
例6 平行线的性质与判定综合
(1)如图所示的四边形ABCD,E是CB延长线上的一点,下列推理正确的是( )
A.如果,那么
B.如果,那么
C.如果,那么
D.如果,那么
【答案】C
(2)已知:如图,,求证:.
【答案】如下图所示:
∵,∴,∴
∵,,∴,
∴.
例7 请你分析下面的题目,从中总结规律,填写在空格上.
(1)如图⑴,已知:,直线分别交、于、,、分别平分、.求证:.从本题能得到的结论是: .
(2)如图⑵,已知:,直线分别交、于、,、分别平分、.求证:.从本题能得到的结论是: .
(3)如图⑶,已知:,直线分别交、于、,、分别平分、,相交与点.求证:.从本题能得到的结是: .
【答案】(1)两直线平行,同位角的角分线也平行;
(2)两直线平行,内错角的角分线也平行;
(3)两直线平行,同旁内角的角平分线互相垂直.
课后创新培养
课后作业
练1 (1)如图,直线AB,CD交于点O,OA平分∠EOC,∠EOC:∠EOD=4:5,则∠BOD= .
(2)如图所示,直线AB交CD于点O,OE平分∠BOD,OF平分∠COB,∠AOD:∠EOD=4:1,则∠AOF= .
【答案】(1)40°;(2)120°.
练2 (1)如图所示,AO⊥BO,CO⊥DO,∠AOC:∠BOC=1:4,则∠BOD= .
(2)如图,若AO⊥CO,BO⊥DO,且∠BOC=α,则∠AOD等于 .
【答案】(1)150°;(2).
练3 如图,是的角平分线,交于点交于点.求证:平分.
【答案】由已知条件可得:,,且,∴,所以 平分.
练4 如图,已知、的平分线相交于,过点且.若,,求、的度数.
【答案】由已知可得:,∵,∴,,∴,.
练5 如图,平分,平分,,,求的度数.
【答案】80°.
课堂思维碰撞
模块一:相交线综合
知识导入
1.在同一平面内,两条直线的位置关系:相交、平行.
注意:我们说的两条直线是指不重合的两条直线.
2.相交直线:
定义:两条直线只有一个公共点,我们称这两条直线为相交线.
如下图,如果直线与直线有公共点,则称直线与直线相交,为交点,其中一条直线是另一条直线的相交线.
性质:相交直线有且只有一个公共点.
3.对顶角:
定义:如果两个角有公共顶点,它们的两边互为反向延长线,具有这种位置关系的两个角叫做对顶角.
定义:两条直线相交成四个角中,有公共顶点而没有公共边的两个角叫做对顶角.如图中,和、和是对顶角.
性质:对顶角相等,如图中:,.
4.邻补角:
定义:两条直线相交所构成的四个角中,有公共顶点且有一条公共边的两个角互为邻补角.如上图,和,和,和,和互为邻补角.
定义:我们也可以说,如果两个角有一条公共边,并且它们的另外一边互为反向延长线,那么这两个角叫做邻补角.
性质:邻补角互补,如上图:,,,.
5.垂线:
如果两条直线相交所成的四个角中有一个是直角,那么就说这两条直线互相垂直,其中的一条直线是另一条直线的垂线,它们的交点为垂足.
如图,直线、互相垂直,垂足为点,记作“于”.
6.三线八角模型:
如图,直线、与相交,也称直线、被直线所截,形成了个小于平角的角,我们通常将这样的几何模型称为“三线八角”.
(1)同位角:两条直线被第三条直线所截,在两条被截直线同旁,在截线同侧的一对角叫做同位角.如上图中:∠1和∠5,形似英文字母“F”.
(2)内错角:两条直线被第三条直线所截,在两条被截直线内部,在截线两侧的一对角叫做内错角.如上图中:∠3和∠5,形似英文字母“Z”.
(3)同旁内角:两条直线被第三条直线所截,在两条被截直线内部,在截线同侧的一对角叫做同旁内角.如上图中:∠4和∠5,形似英文字母“U”.
夯实基础
例1 对顶角、邻补角
(1)如图,∠1和∠2是对顶角的图形是( )
A.甲 B.乙 C.丙 D.丁
(2)如图,∠1与∠2互为邻补角的是( )
A. B. C. D.
(3)如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC:∠EOD=1:2,则∠BOD等于( )
A.30° B.36° C.45° D.72°
(4)已知:如图所示,直线、、交于点,,,则的度数是 .
【答案】(1)C;(2)D;(3)A;(4)60°.
例2 垂直
(1)如图,直线AB、CD相交于点O,OE⊥CD,∠AOE=52°,则∠BOD等于( )
A.24° B.26° C.36° D.38°
(2)如图,已知直线AB,线段CO⊥AB于点O,,的度数为( )
A.15° B.25° C.30° D.45°
(3)如图,直线AB与直线CD相交于点O,OE⊥AB,垂足为O,,则( )
A.150° B.140° C.130° D.120°
(4)在直线AB上任意取一点O,过点O作射线OC、OD,使,当 时,的度数是 .
(5)已知∠α的两边分别与∠β的两边垂直,且∠α=20°,则∠β的度数为 .
【答案】(1)D;(2)C;(3)D;(4)60°或120°;(5)20°或160°.
能力提升
例3 三线八角
(1)如图所示,下列说法错误的是( )
A.∠1与∠2是同旁内角 B.∠1与∠3是内错角
C.∠1与∠5是同位角 D.∠4与∠5互为邻补角
【答案】B
(2)①直线AB和CD被直线AC所截形成的内错角是 ;
②直线AB和CD被直线BE所截形成的同位角是 ;
③∠3和∠6是直线 和 被直线 所截形成的 角;
④∠2和∠6是直线 和 被直线 所截形成的 角.
【答案】①和;②和;③,内错;
④,同旁内角.
(3)如图,用数字表示的角中,同位角有 对,内错角有 对,同旁内角有 对.
【答案】4,4,7.
例4 角度计算
(1)已知:∠MON=132°,射线OC是∠MON内一条射线,且,问OM与OC是否垂直,并说明理由.
(2)如图,,若∠BOC=4∠NOB,且OM平分∠NOC,求∠MON的度数.
【答案】(1),解出,∴.
(2)设,则有,解得:,∴.
模块二:平行线的性质判定进阶
知识导入
1.平行线的定义:
定义:在同一平面内,不相交的两条直线叫做平行线.
如图,如果直线与直线没有公共点,则称直线与直线平行,记作∥,读作平行于.
性质:平行直线在同一平面内,且没有公共点.
易错点:必须强调是在同一平面内.
2.平行线的性质:
性质1:两直线平行,同位角相等.
性质2:两直线平行,内错角相等.
性质3:两直线平行,同旁内角互补.
推论:①两直线平行,同位角的角平分线也平行.
②两直线平行,内错角的角平分线也平行.
③两直线平行,同旁内角的角平分线互相垂直.
3.平行线的判定:
(1)平行线的定义
(2)判定1:同位角相等,两直线平行.
(3)判定2:内错角相等,两直线平行.
(4)判定3:同旁内角互补,两直线平行.
推论:①两直线平行,同位角的角平分线也平行.
②两直线平行,内错角的角平分线也平行.
③两直线平行,同旁内角的角平分线互相垂直.
能力提升
例5 利用平行线性质计算角度
(1)如图,直线l1∥l2∥l3,点A、B、C分别在直线l1、l2、l3上,若∠1=72°,∠2=48°,则∠ABC=( )
A.24° B.120° C.96° D.132°
【答案】 B
(2)如图,,,,则______.
【答案】 20°.
(3)如图,AB∥CD∥EF,CB∥DE∥FG,如果∠1=70°,则∠3的度数为 .
【答案】110°
例6 平行线的性质与判定综合
(1)如图所示的四边形ABCD,E是CB延长线上的一点,下列推理正确的是( )
A.如果,那么
B.如果,那么
C.如果,那么
D.如果,那么
【答案】C
(2)已知:如图,,求证:.
【答案】如下图所示:
∵,∴,∴
∵,,∴,
∴.
例7 请你分析下面的题目,从中总结规律,填写在空格上.
(1)如图⑴,已知:,直线分别交、于、,、分别平分、.求证:.从本题能得到的结论是: .
(2)如图⑵,已知:,直线分别交、于、,、分别平分、.求证:.从本题能得到的结论是: .
(3)如图⑶,已知:,直线分别交、于、,、分别平分、,相交与点.求证:.从本题能得到的结是: .
【答案】(1)两直线平行,同位角的角分线也平行;
(2)两直线平行,内错角的角分线也平行;
(3)两直线平行,同旁内角的角平分线互相垂直.
课后创新培养
课后作业
练1 (1)如图,直线AB,CD交于点O,OA平分∠EOC,∠EOC:∠EOD=4:5,则∠BOD= .
(2)如图所示,直线AB交CD于点O,OE平分∠BOD,OF平分∠COB,∠AOD:∠EOD=4:1,则∠AOF= .
【答案】(1)40°;(2)120°.
练2 (1)如图所示,AO⊥BO,CO⊥DO,∠AOC:∠BOC=1:4,则∠BOD= .
(2)如图,若AO⊥CO,BO⊥DO,且∠BOC=α,则∠AOD等于 .
【答案】(1)150°;(2).
练3 如图,是的角平分线,交于点交于点.求证:平分.
【答案】由已知条件可得:,,且,∴,所以 平分.
练4 如图,已知、的平分线相交于,过点且.若,,求、的度数.
【答案】由已知可得:,∵,∴,,∴,.
练5 如图,平分,平分,,,求的度数.
【答案】80°.
